Глава 1. Теоретическая разработка расчета гидравлической системы

1.1. Методы изучения движения жидкости

Целью изучения движения жидкости является определение кинематических характеристик - скоростей и ускорений, а на их основе - необходимых для решения задач динамических характеристик потока. Существует два принципиально отличных метода изучения движения жидкости. Оба связаны с именами известных математиков и механиков - Ж.Л. Лагранжа и Л. Эйлера [12.С.103].

Рисунок 1.1. Представление о движении жидкости.

*А.

Метод Лагранжа. Этот метод основан на принципе слежения за отдельными материальными объектами - частицами жидкости - при их перемещении в пространстве. Полное представление о движении жидкости в пределах интересующей области может быть получено в том случае, когда объектами наблюдения становятся все заполняющие эту область частицы. Итогом наблюдения за каждой конкретной частицей с начальными координатами Х₀ , У₀ и Z₀ (см. рис. 1.1) на пути ее перемещения в течении времени t - t₀ является след МN, называемый траекторией. Если в результате такого изучения установлено система трех функций

X = X (Хо, У о, Zо, t);

У = У (Хо, Уо, Z₀, t); (1.1)

Z = Z(Хо, Уо,Z ₀,t);

описывающих траекторию каждой частицы, то поставленная цель - получить характеристики кинематики - достигнута, так как из теоретической механики известно, что первые производные этих функций по времени определять компоненты скорости

U_х=dх / dt; U_у = du / dt; U_z = dz / dt,

а вторые производные - ускорения

d²x/ dt² = du_х / dt; d²у / dt² = du_у / dt; d²z/ dt² = du_z / dt;

Метод Эйлера. Этот метод использует принцип наблюдения за изменением скоростей движения жидкости во времени в фиксированных точках пространства. Каждому моменту времени соответствует свое поле скоростей в рассматриваемой области движения жидкости. Полное описание процесса достигается в том случае, когда определены скорости во всех точках этой области за весь период времени наблюдения t. Образно это можно представить как серию последовательных кадров поля скоростей, полученного киносъемкой. Если для данной системы координат X, У, Z определены функции, описывающие изменение поля скоростей и давления во времени

u_х = u_х (х, у, z, t);

u_у = u_у (х, у, z, t);

u_z =u_z (х, у, z, t); (1.2)

p = p (х, У, z, t);

то этим решается одна из основных задач гидродинамики - найти закон распределения скоростей и давления в потоке. Как показало развитие гидравлики, в большинстве случаев метод Лагранжа более сложен и трудоемок, чем метод Эйлера.

Линия и трубка тока, элементарная струйка, вихревая линия, вихревой шнур. Линия тока. Вихревая линия. Проведем через произвольную точку А (см. рис. 1.2) линию АВСD так, чтобы вектор скорости жидкости в данный момент времени t₁ были направлены по касательной к ней в каждой ее точке. Такая линия, в каждой точке которой в данный момент времени вектор скорости направлен по касательной к ней, называется линией тока. Это понятие является центральным в методе Эйлера [12. С. 107].

Рисунок 1.2. Линия тока.

В общем случае неустановившегося движения в следующий момент времени t₂ через ту же точку А может проходить уже другая линия тока АВ₁C₁D₁ и т..д..

Так как вектор скорости и с компонентами u_х, u_у и u_z касателен к линии тока, т.е. совпадает по направлению с элементом линии тока dl, имеющего проекции dx, dy, dz на оси координат, то воспользуемся известным условием параллельности двух векторов - их проекции на оси координат должны быть пропорциональны друг другу.

dx / u_x = dy / u_у = dz / u_z = dl/u (1.3)

Условие (1.3) является уравнением линии тока в дифференциальной форме.

В частном случае при установившемся движении каждая линия тока сохраняет свое положение в пространстве. Она одновременно становится линией, о которой перемещаются частицы, т.е совпадает с траекторией.

Каждая частица жидкости может при своем движении вращаться с угловой скоростью Ω, которая изображается, как известно, вектором, нормальным к плоскости вращения. В поле угловых скоростей Ω в фиксированный момент времени t линия, во всех точках которой векторы Ω направлены к ней по касательным, называется вихревой линией (см. рис. 1.3, а). Так как вектор Ω с компонентами Ω _х, Ω _у, Ω _z совпадает по направлению с элементом длины вихревой линии dl_в, имеющим компоненты dх_в, dу_в, dz_в, то уравнение вихревой линии по аналогии с выражением (1.3) имеет вид

dx_в / Ω_x = dy_в / Ω_в = dz_в / Ω_z = dl_в / Ω.

Рисунок 1.3. Вихревая линия.

В частном случае линии тока могут совпасть с вихревыми линиями. Это имеет место, если во всей области течения векторы угловых и поступательных скоростей параллельны друг другу. Условием такого движения жидкости, называемого винтовым (см. рис. 1.3, б), является соотношение

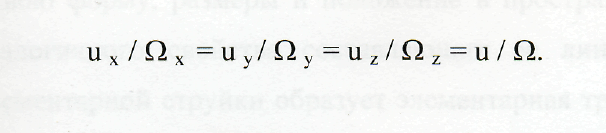
Линии тока и вихревые линии обладают важным свойством — они не могут пересекаться, так как если бы это случилось, то в точке пересечения поступательная и или угловая Ω скорость должна была бы иметь одновременно два направления (по касательной к каждой линии), что невозможно.

Элементарная трубка тока. Вихревая трубка. Если провести линии тока через каждую точку бесконечно малого замкнутого контура dχ (см. рис. 1.4, а), то образуется трубчатая поверхность, называемая элементарной трубкой тока. Элементарная трубка тока обладает важным свойством - в каждой ее точке вектор скорости направлен по касательной к ней. Отсутствие нормальных составляющих скорости исключает массообмен через поверхность элементарной трубки тока. Это свойство - результат того, что элементарная трубка тока образована линиями тока, обладающими тем же свойством - быть касательными к векторам скоростей. Аналогичное образование в поле угловых скоростей называется вихревой трубкой [12. С. 123].

Рисунок 1.4. Элементарная трубка тока.

Элементарная струйка. Вихревой шнур. Линии тока проходят не только через точки контура dχ, но и через все точки ограниченной им площадки dω (см. рис. 1.4, 6). Семейство (пучок) линий тока, проходящие через все точки бесконечно малой площадки, называется элементарной струйкой. При установившемся движении элементарная струйка сохраняет с течением времени постоянными свою форму, размеры и положение в пространстве, что является следствием аналогичного свойства составляющих ее линий тока. Боковую поверхность элементарной струйки образует элементарная трубка тока. Поэтому массообмен через нее исключен и движение жидкости возможно только вдоль элементарной струйки. Если учесть несжимаемость жидкости, то получим следствие, лежащее в основе одного из центральных положений гидравлики - уравнения неразрывности: объем жидкости, прошедший через любое поперечное сечение 1 с площадью dω₁ за время dt., должен равняться объему жидкости, прошедшему через любое другое сечение 2 с площадью dω₂ за то же время.

Невыполнение сформулированного условия привело бы к изменению массы жидкости между сечениями 1 и 2, что противоречит свойствам принятой модели жидкости как несжимаемой однородной среды [12. С. 132].

По аналогии пучок вихревых линий, ограниченный вихревой трубкой, называется вихревым шнуром.

Поток и его элементы. Область движущейся жидкости обычно имеет конечные размеры и называется потоком. Поток можно представить непрерывной совокупностью элементарных струек; такая модель называется струйной моделью потока жидкости.

Живое сечение. Поперечные сечения элементарных струек образуют живые сечения потока (7 на рис. 1.5, а и 2 на рис. 1.5, б).

Рисунок 1.5. Живые сечения потока.

Живое сечение - это поверхность, в каждой точке которой вектор местной скорости направлен к ней по нормали. Площадь такой поверхности со называется площадью живого сечения. Более тщательный анализ свидетельствует о том, что провести поверхность, нормальную ко всем линиям тока, можно не всегда. В таких случаях живое сечение не существует.

Если векторы скоростей всех элементарных струек в живом сечении имеют одно направление, то живым сечением является плоскость, перпендикулярная этому направлению. В инженерной практике при слабой искривленности потока живые сечения, как правило, приближенно предполагают плоскими.

Смоченный периметр. Боковая поверхность струйного потока образуется совокупностью линий тока и поэтому непроницаема для частиц жидкости. В общем случае, как и в рассматриваемом примере, боковую поверхность потока жидкости можно разделить на две характерные части. Одну из них образует смоченная поверхность на контакте боковой поверхности потока со стенками ограничивающего его русла (см. рис. 1.5, а видимая ее часть заштрихована); другую - свободную поверхность - жидкость имеет на границе с атмосферой, а в общем случае - с газообразной средой. Часть контура живого сечения, соприкасающуюся с твердой поверхностью, называют смоченным периметром и обозначают буквой χ (см. рис. 1.5, а, б).

Если русло призматическое, т.е. имеет постоянные по длине форму и размеры сечения, то при равномерном движении площадь смоченной поверхности равна s = χ1 [12. С. 143].

Безнапорные и напорные потоки, струи. Потоки, верхняя часть боковой поверхности которых является свободной, а остальная - смоченной, называются безнапорными (см. рис. 1.5, а). Поток, со всех сторон ограниченный твердыми стенками, называется напорным (см. рис. 1.5, б). Встречаются потоки еще в виде струи, по всей боковой поверхности контактирующие с газообразной или жидкой средой.

У напорных потоков смоченный периметр равен всему периметру живого сечения, у безнапорных он составляет только его часть, а у струй - отсутствует.

Гидравлический радиус. Сила трения жидкости о смоченную поверхность зависит от ее площади s = χ1 (см. рис. 1.5, а). Чем больше смоченная поверхность, тем больше при прочих равных условиях сила трения. Для оценки этого влияния в гидравлике широко используется понятие гидравлического радиуса - отношения площади живого сечения к смоченному периметру:

Эта величина характеризует удельную, т.е. приходящуюся на единицу длины смоченного периметра, площадь живого сечения. Легко сделать вывод, что поток с наибольшим гидравлическим радиусом при прочих равных условиях имеет минимальную силу трения, приложенную к смоченной поверхности.

Как известно из геометрии, из всех фигур минимальным периметром при одной и той же площади обладает круг. Следовательно, напорные потоки круглого сечения по сравнению с потоками другой формы живого сечения имеют наибольший гидравлический радиус и минимальное сопротивление движению (см. рис. 1.6, а). Это обстоятельство и объясняет применение труб круглого сечения.

Рисунок 1.6. Гидравлический радиус.

Среди безнапорных таким свойством обладают потоки полукруглого сечения (см. рис. 1.6, б). Однако выполнить канал такого сечения часто мешает ряд серьезных препятствий: технологическая сложность изготовления, невозможность сохранения такой формы в естественном грунте без укрепления, необходимость поддерживать постоянное наполнение канала до половины диаметра и т.д. Если для создания безнапорных потоков и используются трубы круглого сечения, например, в качестве дорожных водопропускных труб, коллекторов ливневой канализации и др., то их заполнение обычно превышает половину диаметра, а гидравлический радиус не достигает наибольшего значения. В большинстве случаев безнапорные каналы имеют трапецеидальную или прямоугольную форму живого сечения [13. С. 305].

Равномерное и неравномерное движение. Критерием равномерного движения является сохранение телом постоянной скорости вдоль пути. При равномерном и прямолинейном движении не меняется и ее направление, что равносильно отсутствию ускорения. Применительно к потоку жидкости это условие может быть конкретизировано следующим образом. Движение потока можно считать равномерным и прямолинейным, если каждая его частица движется прямолинейно с постоянной скоростью вдоль своей траектории, причем траектории всех частиц параллельны. Следовательно, все элементарные струйки в этом случае параллельны, поток сохраняет форму и размеры живого сечения, т.е. он является цилиндрическим. Живые сечения у него плоские. В нем сохраняется закон сохранения скоростей - их эпюра по живому сечению не изменяется вдоль потока, например в продольном сечении канала вертикальной плоскостью хОz (см. рис. 1.7).

Если при установившемся движении, являющимся необходимым условием равномерного движения, скорости вдоль отдельных струек изменяются, то такое движение называется неравномерным. Как будет показано ниже, в этом случае неравномерность движения обязательно ведет к изменению размеров и/или формы живого сечения вдоль потока, например на реке перед мостом или другим подпорным гидротехническим сооружением, в частности плотиной.

Рисунок 1.7. Равномерное и неравномерное движение.

Пространственный, плоский и одномерный потоки. В природе существуют лишь потоки, скорость течения которых зависит от всех трех пространственных координат х, у, z. Поэтому их называют трехмерными или пространственными. В некоторых случаях при решении инженерных задач трехмерный поток можно заменить той или иной упрощенной моделью.

Если течение происходит так, что линия тока расположены в параллельных плоскостях и имеют одинаковую форму (см. рис. 1.8), а скорости в сходственных точках одинаковы, то такой поток называют плоским. Для изучения плоского потока достаточно проанализировать его течение лишь в одной из плоскостей, а во всех остальных оно будет таким же [13. С. 356].

Рисунок 1.8. Плоский поток.

Очевидна, что компонента скорости, нормальная к плоскости течения, равна нулю, а две другие зависят лишь от двух пространственных координат. Поэтому плоские потоки называют также двумерными. Например, если течение происходит в плоскости хОу, то u_z = 0; u_x = u_х (х, у); u_у = u_у (х, у). Конечно, при неустановившемся движении скорости u_х и u_у зависят еще и от времени t.

Еще более грубую схематизацию потока получим, если во всех его живых сечениях заменить действительные скорости средними скоростями. В такой модели средняя скорость может зависеть лишь от одной пространственной координаты - расстояния 1 вдоль потока, т.е. v = v (1).Такую модель называют одномерным потоком. Ясно, что в одномерном потоке средняя скорость может кроме 1 зависеть и от времени: v = v (t, 1) [12. С. 342].

Одномерный поток является наиболее простой моделью потока, однако упрощения, полученные при ее введении, позволяют получить сравнительно простым путем ответ на многие интересующие инженера вопросы. Иногда такой информации оказывается вполне достаточно для принятия необходимого решения, иногда можно ее скорректировать, иногда, если она оказывается слишком грубой, следует обращаться к более сложным моделям потока.

Для равномерного одномерного потока v = const, для неравномерного v = v (1),для неравномерного и неустановившегося v = v (t,1).