2.5.5. Амплитудно-частотные характеристики
Выполняем анализ по переменному току с учетом изменения температуры в диапазоне, указанном в п. 2.5.3. Для этого сначала открываем окно анализа AС (рис. 43).
Рис. 43
В поле Temperature задаем через запятую три параметра: верхний предел температуры, нижнее значение температуры и шаг изменения температуры (рис. 44).
Рис. 44
Запуская анализ, получаем семейство характеристик (рис. 45).
Рис. 45
Шесть
линий, изображенных на нижней часть
рисунка 45, представляет собой АЧХ при
шести значениях температуры: +10 °С, +15
°С, +20 °С, +25 °С, +30 °С, +35 °С. График,
изображенный на нижней части рисунка
45, получается путем увеличения фрагмента
графика. Фрагмент выделяем левой кнопкой
мыши в режиме Scale
Mode.
В режим входим включением кнопки
или нажатием F8.
Нажав
кнопку
или
F7,
переходим в режим отображения курсоров
(рис. 46). Мы видим, что одна из линий АЧХ
выделена серым цветом, и над графиком
указано, что выделенная зависимость
соответствует температуре 35 °С.
При нажатии навигационных клавиш ↑, ↓ выделение цветом смещается от одной линии к другой, и над графиком изменяется информация о температуре.
Рис. 46
Нажав
кнопку
(Run)
или клавишу F5,
мы получим график в исходном частотном
диапазоне. Нажав клавишу F8,
перейдем в режим отображения курсоров.
Один курсор находится на левой границе
диапазона частот (10 Гц), а другой – на
правой границе (10 кГц, рис. 47).
Рис. 47
Из рисунка видно, что при температуре +10 °С неравномерность АЧХ в полосе пропускания составляет приблизительно 0,612 дБ. Нажимая навигационные клавиши ↑, ↓, мы видим, что над графиком изменяется информация о температуре, а под графиком изменяется информация о неравномерности АЧХ. Перебирая все значения температуры, мы находим, что при температуре +35 °С амплитудно-частотная характеристика имеет наибольшую неравномерность (0,617 дБ).
2.5.6. Зависимость параметров фильтра от температуры
2.5.6.1. Зависимость неравномерности ачх от температуры
Зависимость параметров фильтра от температуры удобно получать в одном из режимов частотного анализа. Этот режим называется параметрическая зависимость (Performance Window). Находясь в режиме частотного анализа (рис. 47), выбираем меню: AC→Performance Windows→Add Performance Window… (рис. 48).
Рис. 48
В результате мы попадаем в окно редактирования свойств параметрической зависимости (рис. 49). По умолчанию предлагается исследовать зависимость времени нарастания сигнала с помощью функции Rise_Time().
После
нажатия кнопки Get
(см. рис. 49) открывается окно получения
функции зависимости (Get
Performance
Function),
в котором нужно нажать на кнопку
(рис. 50), чтобы раскрыть выпадающий
список функций (рис. 51).
Рис. 49
Рис. 50
Рис. 51
В списке функций выбираем функцию High_Y(), возвращающую максимальное значение (рис. 52). И так как в качестве выражения указано db(v(In)/v(Out)), то функция будет возвращать максимальное значение ослабления сигнала (в децибелах).
а) б)
Рис. 52
Нажатие клавиши ОК (рис. 52, б) приведет к тому, что выделенный текст «Rise_Time(db(v(In)/v(Out)),1,1,1,2)» в поле «What To Plot» (рис. 53) заменяется новым текстом «High_Y(db(v(In)/v(Out)),1)» (рис. 54). При этом курсор находится после вставленного текста.
Рис. 53
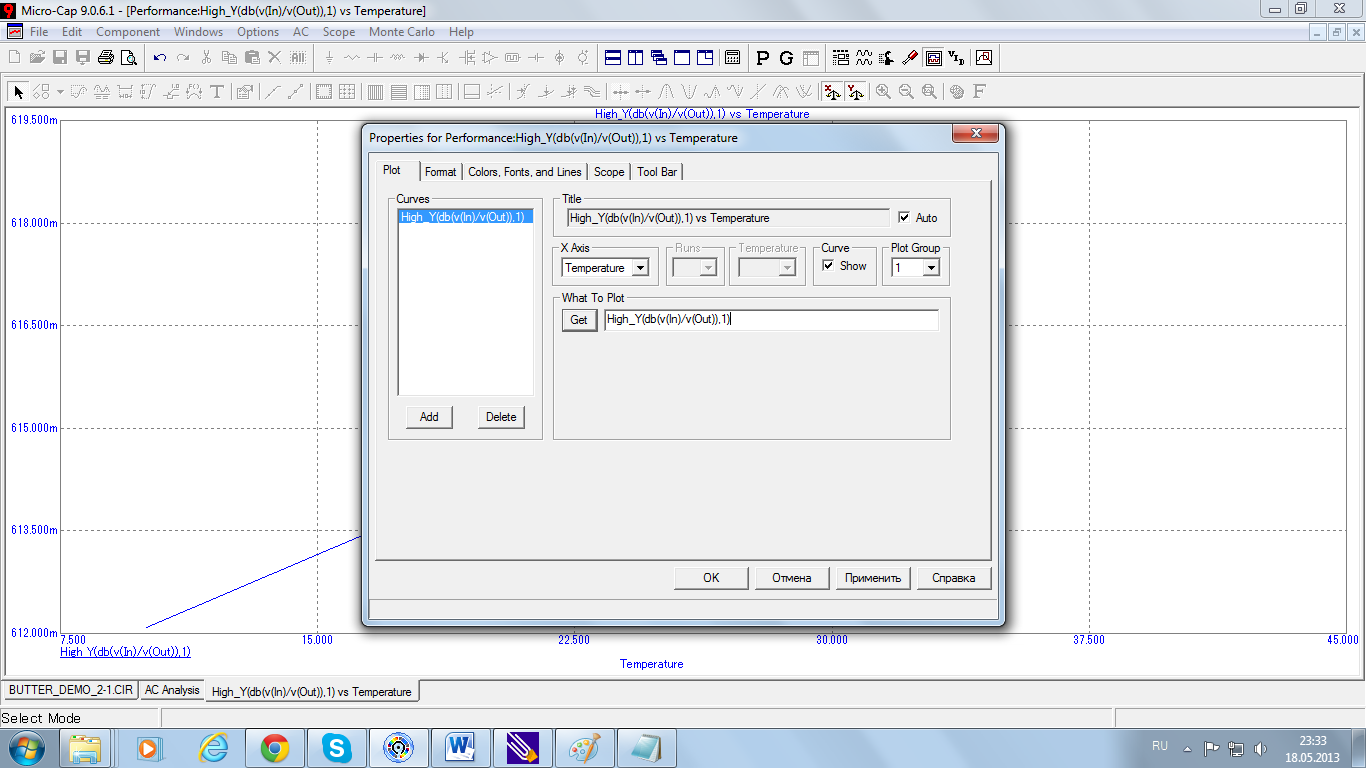
Рис. 54
Затем ставим после функции знак минуса, затем нажимаем кнопку Get (рис. 55) и из списка выбираем функцию Low_Y().
Рис. 55
В результате в поле What To Plot вписана формула
High_Y(db(v(In)/v(Out)),1)-Low_Y(db(v(In)/v(Out)),1),
задающая разность максимального и минимального значений затухания в децибелах (рис. 56). После нажатия кнопки ОК получаем график зависимости неравномерности АЧХ от температуры (рис. 57).
Рис. 56
Рис. 57
По нажатию клавиши F8 появляются курсоры, отображающие неравномерность АЧХ на границах диапазона температур: 0,612 дБ при 10 °С и 0,617 дБ при 35 °С.
Рис. 58
Таким образом, фильтр, построенный на электрорадиоэлементах из ряда E96, в заданном диапазоне температур имеет максимальную неравномерность АЧХ в полосе пропускания равную 0,617 дБ, что меньше заданной максимальной неравномерности (1 дБ). Полученное значение неравномерности не учитывает класс точности электрорадиоэлементов (ЭРЭ).