7.2. Транзисторные автогенераторы

7.2.1. Условия самовозбуждения

Транзисторный АГ можно рассматривать как усилитель, охваченный положительной обратной связью: на вход транзистора подаются колебания не от внешнего источника, а из собственного контура через цепь обратной связи. При правильном выборе конфигурации и параметров цепи обратной связи такой усилитель оказывается генератором с самовозбуждением (АГ).

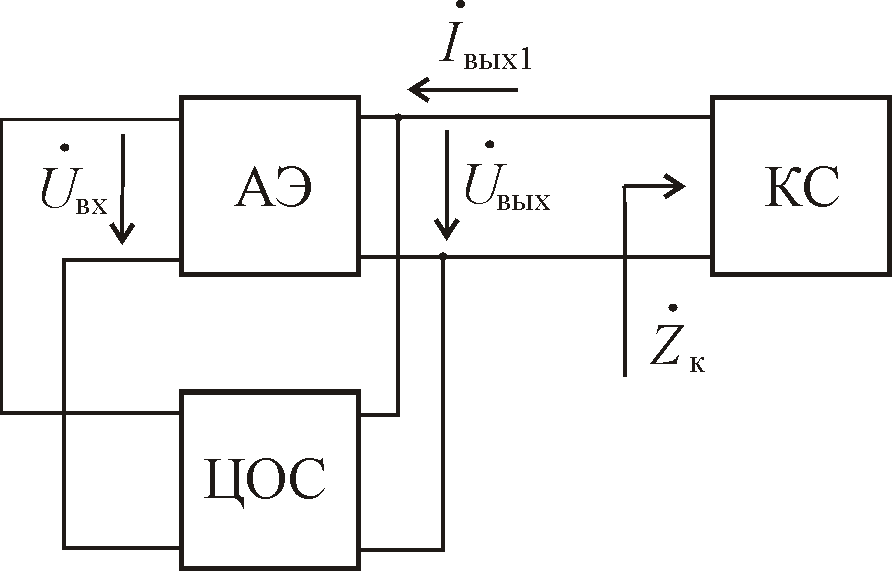
Таким образом, структура АГ (по переменной составляющей тока) может быть отображена схемой, показанной на рис. 7.1. К выходным электродам

транзистора (АЭ) подключена колебательная система (КС) с эквивалентным сопротивлением к, часть напряжения с которой подводится через цепь обратной связи (ЦОС) ко входным электродам транзистора. При разомкнутой цепи обратной связи выходное напряжение (напряжение на сопротивлении к) равно вых= – вых1 к (7.1)

Рис. 7.1. Структурная схема АГ

Знак «–» в формуле (7.1) учитывает, что полярность (фаза) напряжения U_вых на рис. 7.1 противоположна направлению первой гармоники выходного тока I_вых1.

Амплитуда этого тока связана с напряжением на входе транзистора _вх формулой

_вых1 = _{ср вх}, (7.2)

где _ср – средняя крутизна транзистора, т.е. крутизна по первой гармонике.

Комплексность _ср означает, что амплитуда первой гармоники выходного тока, вообще говоря, не синфазна напряжению _вх. При записи (7.2) предполагалось, что влияние _вых на _вых1 пренебрежимо мало.

При замыкании цепи обратной связи

_вх= – _{ос вых}, (7.3)

где _ос – коэффициент передачи четырехполюсника ЦОС. Знак «–» в последней формуле означает, что напряжение _вх в схеме АГ должно иметь полярность (фазу), противоположную показанной на рис. 7.1. Как будет показано ниже, это достигается соответствующим построением четырехполюсника ЦОС.

Из соотношений (7.1) – (7.3) следует, что в АГ должно выполняться равенство:

_{ср к ос}=1. (7.4)

Это соотношение называют уравнением стационарного режима АГ, так как оно определяет условия существования незатухающих автоколебаний с определенными амплитудой и частотой.

Если представить величины в (7.4) в комплексной форме:

_{, , ,}

то из уравнения (7.4) следуют два условия:

S_срZ_кК_ос = 1, (7.5)

φ_s + φ_к + φ_ос = 2πn, n = 0, 1, 2... . (7.6)

Первое из них называется уравнением баланса амплитуд, а второе – уравнением баланса фаз.

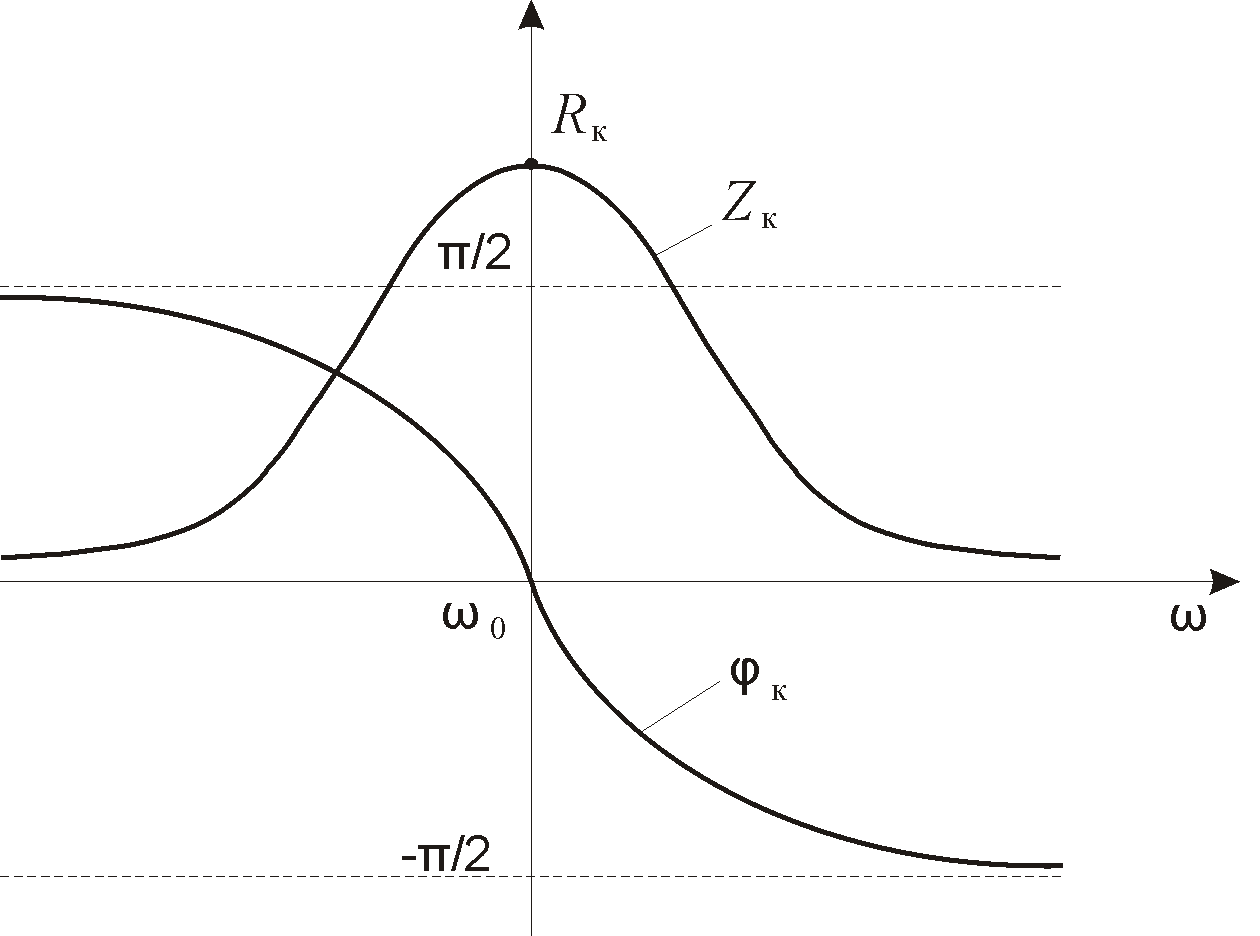
Рассмотрим величины, входящие в формулы (7.5) и (7.6). Величины Z_к и φ_к определяются схемой КС автогенератора и слабо зависят от амплитуды автоколебаний и режима транзистора. В первом приближении этой зависимостью можно пренебречь. Если в качестве КС используется параллельный колебательный контур, что обычно имеет место в схемах АГ, то частотная зависимость Z_к(ω) и φ_к(ω) имеет вид, показанный на рис. 7.2.

Рис. 7.2. Частотная зависимость Zк и φк; ω0 – резонансная частота, Rк – резонансное значение сопротивления колебательного контура

Величины Кос и φос определяются схемой четырехполюсника ЦОС. Однако, поскольку параллельно зажимам ЦОС включается входная проводимость транзистора, она может оказывать влияние на Кос и φос. Как следствие, эти величины, вообще говоря, зависят от режима транзистора и амплитуды автоколебаний. В первом приближении этой зависимостью пренебрегают. Частотные зависимости Кос(ω) и φос(ω) обусловлены тем, что в состав ЦОС входят как реак-

тивные, так и активные сопротивления. В качестве последних выступают активная составляющая входного сопротивления транзистора, а также элементы его цепи питания (цепи смещения). Из-за влияния этих активных сопротивлений в реальных условиях всегда фазовый угол φ_ос≠0. Однако на умеренно высоких частотах величина φ_ос мала.

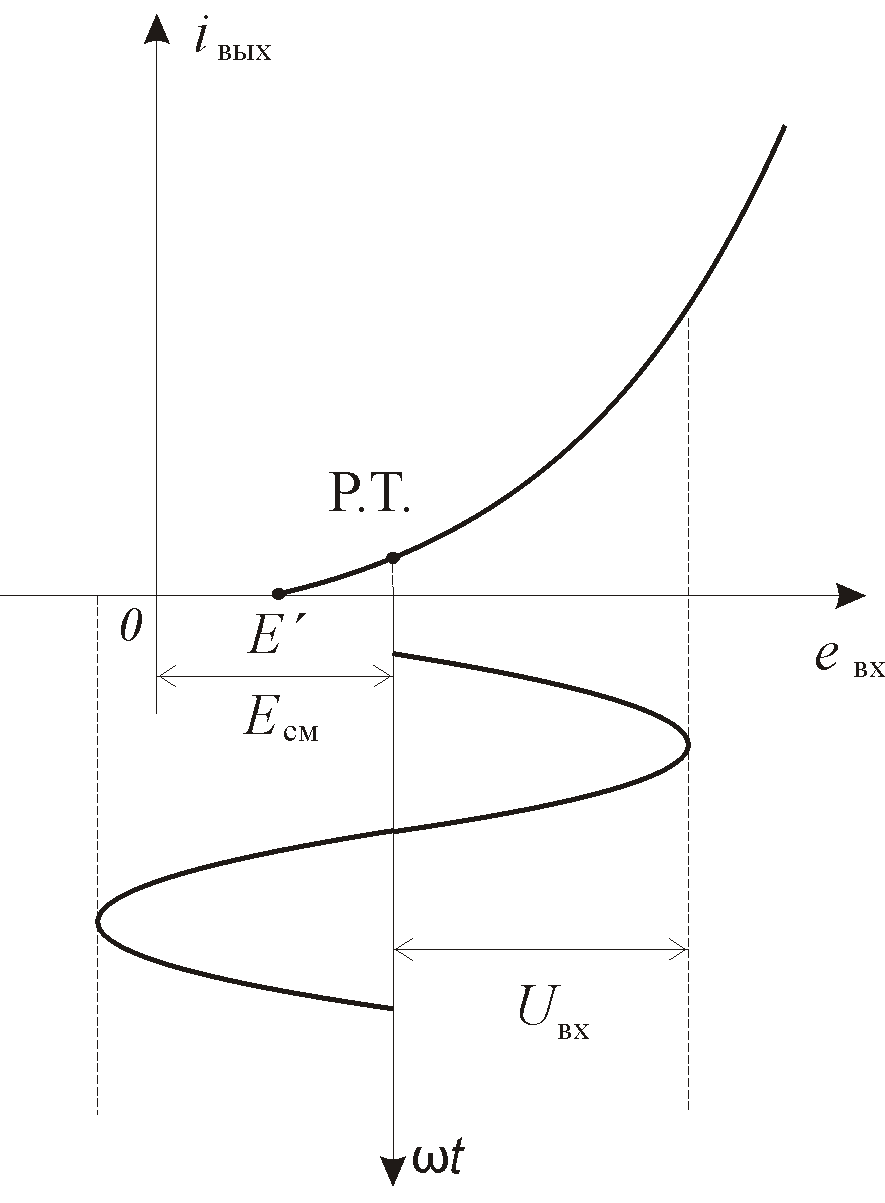
Величина S_ср=I_вых1/U_вх зависит, во-первых, от средней за период входного колебания крутизны проходной характеристики транзистора i_вых=f(e_вх) (см. рис. 7.3). Очевидно, что эта усредненная крутизна характеристики определяется положением его рабочей точки (Р.Т.), т.е. значением напряжения смещения Е_см на входном электроде и амплитудой U_вх. Во-вторых, величина S_ср зависит от режима транзистора. Действительно, при достаточно большой амплитуде колебаний (как U_вх, так и U_вых) транзистор переходит в перенапряженный режим. При этом, как известно, в импульсе выходного тока появляется провал и как следствие уменьшается амплитуда первой гармоники I_вых1. Соответственно

при переходе транзистора в перенапряженный режим всегда происходит уменьшение Sср независимо от положения его Р.Т. Величина угла φs, определяющая фазовый сдвиг выходного тока относительно входного напряжения, вследствие инерционности транзистора как активного элемента всегда отрицательна: φs<0. Как известно (см. ОК, часть 1), φs= φs(ω), причем с ростом частоты φs увеличивается. Однако при работе на частотах много меньших предельных значений для данного транзистора фазовый угол φs мал. Как следует из изложенного, в уравнении (7.6) все входящие

Рис. 7.3. К определению средней крутизны транзистора

величины являются функциями частоты, но в первом приближении слабо зависят от амплитуды колебаний. Поэтому уравнение баланса фаз используется для определения частоты колебаний.

Рассмотрим приближенное решение уравнения фазового баланса. Входящие в уравнение (7.6) фазовые углы имеют существенно разную степень частотной зависимости: при высокой добротности колебательного контура скорость изменения φ_к(ω), определяемая графиком на рис. 7.2, значительно больше, чем φ_s(ω) и φ_ос(ω). На этом основании при решении уравнения (7.6) можно принять: φ_s(ω) + φ_ос(ω) = φ_s,ос(ω) ≈ const. Уравнение принимает вид

φ_к(ω) = - φ_s,ос(ω). (7.7)

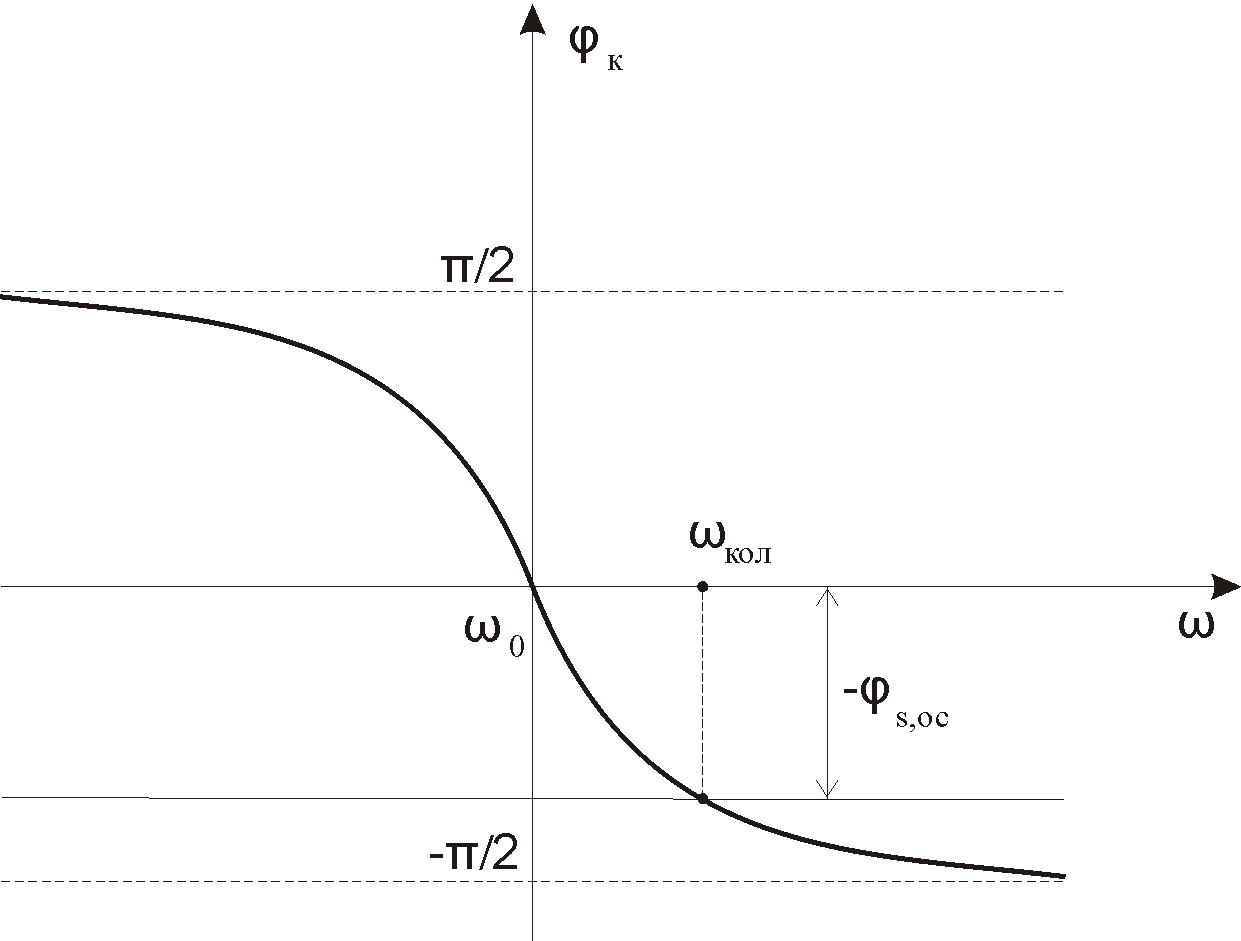
Определение из уравнения (7.7) частоты колебаний АГ ω_кол графически показано на рис. 7.4.

Из этого рисунка следует, что, с одной стороны, частота колебаний ω_кол ≠ ω₀. Равенство будет иметь место лишь в случае, когда φ_s,ос=0. С другой стороны, частота ω_кол достаточно близка к резонансной частоте колебательного контура, поскольку крутизна характеристики φ_к(ω) в окрестности этой частоты велика. Можно сказать, что частота колебаний АГ определяется частотой ω₀, хотя, строго говоря, никогда не равна ей.

Уравнение баланса амплитуд (7.5) можно представить в виде

S_ср = 1/Z_y, (7.8)

где величина Z_y = Z_кК_oc носит название управляющего сопротивления АГ. Урав-

Рис. 7.4. Приближенное решение уравнения фазового баланса

нение (7.8) позволяет найти амплитуду установившихся колебаний, поскольку, как отмечалось, от нее зависит средняя крутизна Sср транзистора. Вид зависимости Sср(Uвх) можно определить из рис. 7.3. Этот вид существенно зависит от положения рабочей точки Р.Т. транзистора, т.е. от соотношения напряжений смещения Есм и отсечки Е´. При положении Р.Т., показанном на рис. 7.3, зависи-

мость S_ср(U_вх) качественно изображена на рис. 7.5, а. При U_вх≈0 средняя крутизна определяется локальной крутизной S₀ характеристики i_вых = f(e_вх) вблизи рабочей точки. При увеличении амплитуды U_вх транзистор заходит в режим с отсечкой тока и средняя за период колебаний величина крутизны уменьшается. При достаточно большой амплитуде U_вх за счет перехода транзистора в перенапряженный режим S_ср стремится к нулю.

Если Е_см<Е´ (в частности, Е_см<0), зависимость S_ср(U_вх) имеет вид, показанный на рис. 7.5, в. При малых U_вх средняя крутизна равна нулю, так как транзистор находится в отсечке. При увеличении U_вх происходит частичное отпирание транзистора и S_ср растет. Затем при больших значениях U_вх средняя крутизна начинает уменьшаться из-за перехода транзистора в перенапряженный режим. Рис. 7.5, б соответствует промежуточному случаю Е_см≈Е´.

В схемах АГ применяется автоматическое смещение. Поэтому величина Е_см в процессе самовозбуждения меняется таким образом, что Р.Т. (см. рис. 7.3) постепенно сдвигается влево. Как следствие, в процессе самовозбуждения вид зависимости S_ср(U_вх) плавно изменяется от рис. 7.5, а к рис. 7.5, б или даже к рис. 7.5, в, если транзистор заходит в режим работы с отсечкой тока.

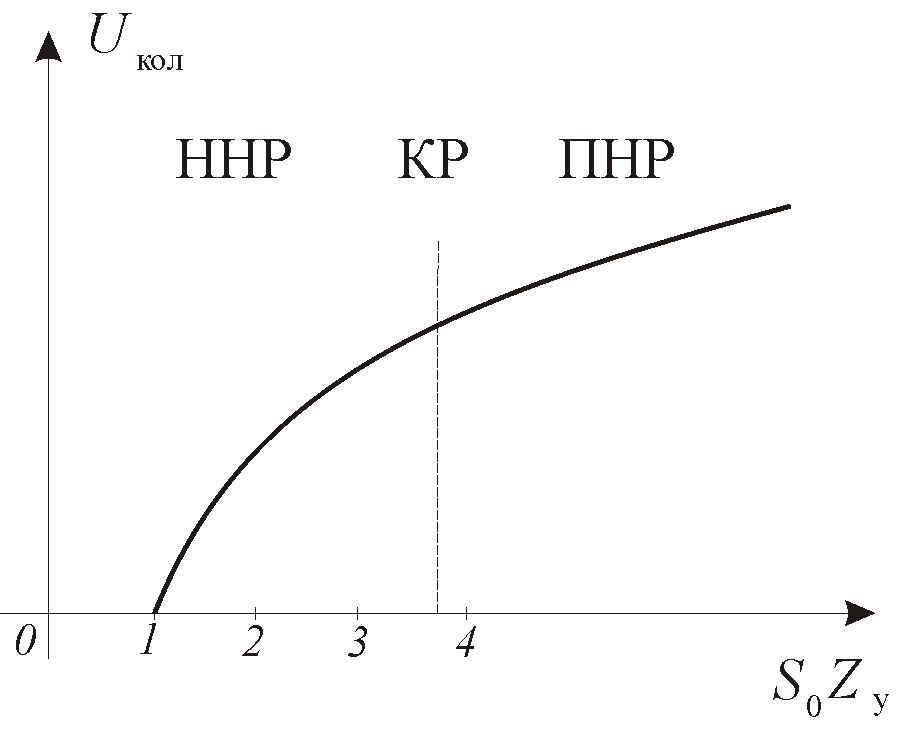
Рассмотрим графическое решение уравнения баланса амплитуд (7.8) для случая, показанного на рис. 7.5, а. Амплитуда стационарных колебаний U_кол соответствует точке пересечения графика S_ср(U_вх) и прямой 1/Z_y,. Очевидно, для самовозбуждения АГ необходимо выполнить условие: S₀>1/Z_y (или S₀Z_y>1). При S₀Z_y≤1 самовозбуждение невозможно. Зависимость амплитуды стационарных колебаний U_кол от величины S₀Z_y, называемая нагрузочной характеристикой АГ, показана на рис. 7.6. Из рисунка видно, что для того, чтобы обеспечить в стационарном состоянии недонапряженный режим АГ (это необходимо для получения гармонических колебаний с высокой стабильностью частоты), следует взять S₀Z_y=2…3.

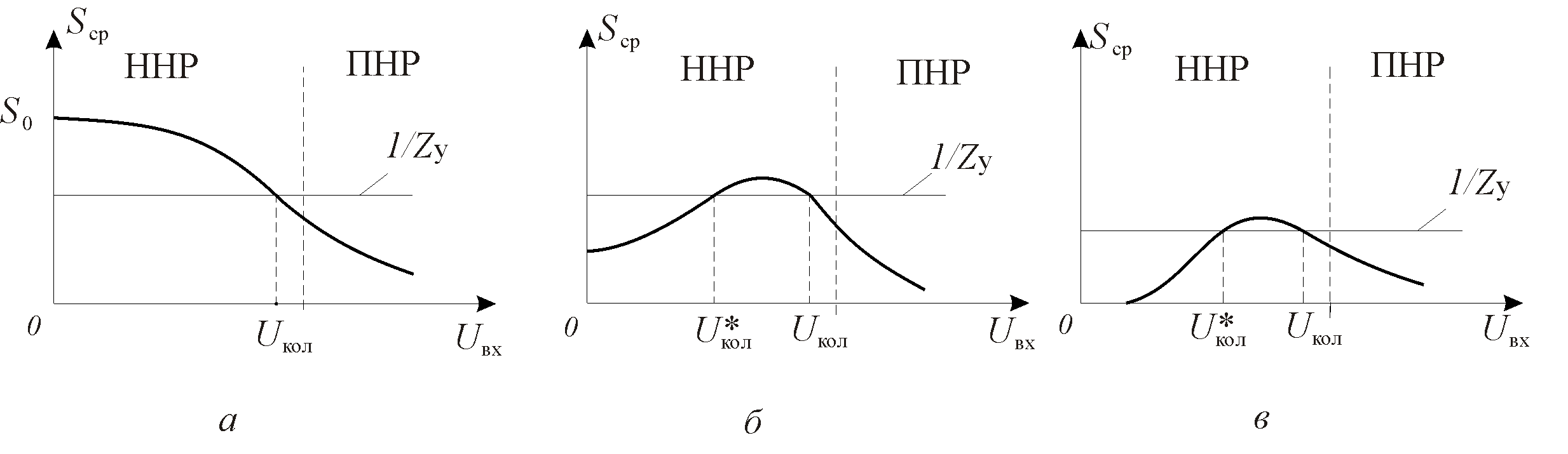
Рис. 7.5. Зависимость средней крутизны от амплитуды колебаний при разных

положениях Р.Т. (а – Е_см>Е´; б – Е_см≈Е´; в – Е_см<Е´ ) и графическое решение

уравнения баланса амплитуд

Решение уравнения баланса амплитуд (7.8) при двух других видах зависимости Sср(Uвх) показано на рис. 7.5, б, в. Из рисунков видно, что в этих двух случаях у графика Sср(Uвх) имеется две точки пересечения с линией 1/Zy, соответствующие значениям амплитуды Uкол и U*кол Однако, как показывает анализ, устойчивому стационарному режиму АГ соответствует лишь первое значение. Графики, изображенные на рис. 7.5, а – в, позволяют проанализировать процесс самовозбуждения АГ и установле-

Рис. 7.6. Нагрузочная характеристика АГ

ние колебаний в нем. Случаю, показанному на рис. 7.5, а, соответствует «мягкий» режим самовозбуждения, т.е. самовозбуждение от малых флуктуаций U_вх. При U_вх=0 S_ср = S₀>1/Z_y. Это означает, что энергия, вносимая в колебательный контур активным элементом (транзистором), превышает ее потери в колебательном контуре. Поэтому при выполнении условия баланса фаз (7.6) достаточно небольших флуктуаций U_вх, чтобы произошло самовозбуждение и амплитуда колебаний АГ U_вх начала нарастать.

В процессе нарастания U_вх в соответствии с характеристикой S_ср(U_вх) средняя крутизна уменьшается, т.е. ослабляются усилительные свойства транзистора. При достижении U_вх=U_кол оказывается выполненным условие баланса амплитуд (7.8). Это означает, что энергия, вносимая в колебательный контур, равна потерям в нем. В АГ устанавливается стационарный режим с амплитудой колебаний U_кол Очевидно, что для облегчения процесса самовозбуждения величина S₀Z_y, характеризующая запас по самовозбуждению, должна быть достаточно велика. Это достигается выбором положения Р.Т. на достаточно крутом участке проходной характеристики транзистора (см. рис. 7.3).

Нетрудно видеть, что в случаях, показанных на рис. 7.5, б, в, «мягкое» самовозбуждение невозможно. При малых флуктуациях U_вх потери энергии в колебательном контуре превышают ее поступление и состояние U_вх=0 является устойчивым. Самовозбуждение произойдет лишь тогда, когда на вход транзистора от внешнего генератора хотя бы кратковременно будет подано напряжение с амплитудой большей, чем U^*_кол. Тогда в АГ будет выполнено условие самовозбуждения S₀Z_y>1. Амплитуда U_вх начнет нарастать и достигнет в стационарном режиме значения U_кол. Такой режим самовозбуждения (от внешнего «толчка») называется «жестким». Он не находит применения в схемах АГ. Однако вид зависимостей S_ср(U_вх), показанный на рис. 7.5, б, в, представляет практический интерес, поскольку, как отмечалось, он характерен для отдельных этапов установления колебаний в АГ с автоматическим смещением.