7.5. Состав возбудителя передатчика и его функции

Как уже указывалось, в состав современного возбудителя, помимо автогенератора (или синтезатора частот), входит формирователь видов работ (ФВР). При угловой модуляции (манипуляции) передача информации связана с изменением частоты (фазы) колебаний; управление колебаниями, естественно, осуществляется непосредственно в возбудителе. В радиопередатчиках с амплитудной модуляцией (АМ) управление колебаниями по энергетическим соображениям чаще всего производится в оконечном или предоконечном каскадах (см. раздел 6).

Тем не менее, в сложных современных возбудителях все же предусматриваются режимы АМ или АМН (амплитудной манипуляции) либо в целях универсализации возбудителя, либо как резервные виды работ. Режим АМН осуществляется за счет выходного аттенюатора с электронным цифровым управлением от блока ФВР. Однополосная модуляция с полностью или частично подавленным несущим колебанием с использованием верхней или нижней полосы, реализуется фильтровым методом непосредственно в возбудителе передатчика (см. раздел 6).

В простейших возбудителях формирование требуемого вида работ производится непосредственно на рабочих частотах, т. е. в возбудителе нельзя отдельно выделить формирователь вида работ. Например, в синтезаторе частот с ДПКД (см. рис. 7.20) можно осуществить частотную модуляцию, вводя информационный сигнал непосредственно на вход РЭ. Однако в этом случае необходимо предусмотреть подавление нижней модулирующей частоты f_{н. мод} в петле ФАПЧ выбором частоты среза ФНЧ f_ФНЧ <<f_{н. мод}. При этом возможно существенное уменьшение полосы захвата ФАПЧ при сохранении полосы удержания и режима стабилизации частоты f_ПГ по частоте ЭГ.

С увеличением числа каналов и диапазона рабочих частот возбудителя, формирование вида работ и опорных частот становится целесообразным производить в самостоятельных блоках. Это объясняется тем, что совмещение указанных функций усложняет получение требуемого подавления побочных составляющих на выходе возбудителя, особенно если возбудитель работает в широком диапазоне частот.

По указанной причине в современных возбудителях ввод информации (формирование требуемых видов работ) выполняется на фиксированной частоте поднесущего колебания f_пн, а в тракте переноса сформированные колебания преобразуются в рабочий диапазон частот с помощью переменной опорной частоты f_оп, поступающей с синтезатора частот: f_раб = f_пн + f_оп .Тракт переноса сформированных колебаний может содержать несколько смесителей.

8. Радиопередатчики с угловой модуляцией

8.1. Общие соотношения при чм и фм. Спектры сигналов.

Показатели качества

Угловая модуляция (УМ) может быть частотной (ЧМ) или фазовой (ФМ). УМ применяется в системах низовой радиосвязи различных диапазонов частот, в радиовещании на УКВ, в звуковом сопровождении телевизионного вещания, в наземной радиорелейной связи прямой видимости, тропосферной и космической связи. Кроме того, УМ используется в радиотелеметрии, в системах радиоуправления, некоторых системах радионавигации и радиолокации. Телеграфные сигналы и цифровая информация в настоящее время передаются преимущественно путем частотной и фазовой манипуляции.

Поскольку при ЧМ и ФМ амплитуда радиосигнала постоянна, эти виды модуляции обеспечивают лучшую помехоустойчивость и более высокие энергетические характеристики, чем АМ, однако для этого им требуются бóльшие эффективные полосы частот.

При УМ изменяется во времени полная фаза высокочастотного колебания, т.е. аргумент :

,

где ω₀ – центральная или средняя частота УМ; – фаза, зависящая от модулирующего сигнала. Поскольку полная фаза связана с мгновенной частотой соотношениями

; , (8.1)

то изменение в общем случае вызывает изменение (t), а изменение частоты всегда сопровождается изменением фазы.

Модулирующий сигнал U_мод (t) в общем случае имеет сложную форму, и анализ процессов, происходящих в передатчике, затруднен. Многие задачи решаются просто, если считать, что модуляция производится одним тоном. В этом случае УМ-сигналы будем представлять выражением

, (8.2)

где U_m – амплитуда ВЧ колебания (U_m = const);  – частота модулирующего колебания; m – индекс модуляции.

Модуляция называется фазовой, если по закону модулирующего сигнала изменяется фаза :

, (8.3)

– девиация (амплитуда изменения) фазы. В этом случае индекс модуляции пропорционален амплитуде модулирующего сигнала и не зависит от его частоты:

(8.4)

(k_ – коэффициент пропорциональности).

Модуляция называется частотной, если по закону модулирующего сигнала изменяется частота ω:

. (8.5)

В этом случае девиация частоты , т.е. отклонение ее от среднего значения , прямопропорциональна и не зависит от частоты :

. (8.6)

В (8.5) так же, как в (8.3), закон модуляции является гармоническим, но в отличие от (8.3) принят косинусоидальным из удобства получения последующих выражений.

Используя соотношения (8.1) находим

для ФМ:

; (8.7,а)

для ЧМ:

. (8.7,б)

Из этих выражений видно, что при ФМ при неизменной амплитуде модулирующего сигнала (и соответственно индексе модуляции ) девиация частоты увеличивается пропорционально частоте модулирующего сигнала или, как принято говорить, увеличивается со скоростью 6 дБ на октаву. При ЧМ при неизменном значении (и, соответственно, ) индекс модуляции уменьшается пропорционально частоте : .

Как известно [3], при модуляции одним тоном спектры ФМ- и ЧМ- колебаний линейчатые, содержат составляющую средней частоты и множество составляющих боковых частот ( p = 1, 2, 3, …). Относительные амплитуды составляющих спектра пропорциональны функциям Бесселя первого рода J_p(m) порядка p от аргумента m:

.

Спектры сигналов при m = 1,4 и 8 представлены на рис.8.1 в качестве примера. Цифры около спектральных составляющих означают их значения в процентах относительно немодулированной несущей.

а б

в

Рис. 8.1. Спектры сигналов с угловой модуляцией при различных индексах модуляции

Характер зависимости функций Бесселя от аргумента представлен графиками на рис. 8.2. При J_p < 0 соответствующие спектральные составляющие изменяют фазу на 180°, что не отражено на рис. 8.1. Отметим, что функция J₀(m) проходит через нуль при m ≈ 2,4; 5,5; 8,6; … . Отсюда следует, что составляющая спектра с частотой может отсутствовать. По этой причине частоту называют средней или центральной частотой ЧМ-сигнала, а не несущей, как ее называют в спектре АМ-колебаний. Амплитуды боковых составляющих имеют максимум при p  m, а при p > m быстро убывают с увеличением p (см. рис. 8.2).

При угловой модуляции средняя мощность модулированного колебания не изменяется по сравнению с мощностью немодулированного колебания частоты , так как амплитуда остается постоянной. Однако происходит значительное перераспределение мощностей между составляющей и боковыми составляющими, причем при m > 1 основная часть мощности приходится на долю боковых составляющих, которые несут информацию. Этим и объясняются более высокая помехоустойчивость и хорошие энергетические показатели при угловой модуляции.

Как видно из спектрограмм на рис. 8.1, с ростом m энергия УМ-сигнала распределяется по большему числу боковых составляющих. Поэтому для повышения помехоустойчивости желательно использовать УМ-сигналы с m>>1. Поскольку, как было показано, при ЧМ индекс модуляции убы-вает с ростом частоты модуляции F, на верхних модулирующих частотах ухудшается соотношение сигнал-шум принимаемого сигнала, что ведет к

Рис. 8.2. Графики функций Бесселя первого ряда порядка р

снижению качества в вещании или помехоустойчивости в связи. Для устранения этого недостатка обычно применяют предварительную коррекцию модулирующего сигнала таким образом, чтобы с возрастанием F пропорционально возрастала его амплитуда (это называется коррекция 6 дБ на октаву). При такой коррекции девиация частоты увеличивается с ростом F, что характерно для ФМ-сигнала (см. формулу (8.7, а)). В этом случае ЧМ передатчик, по существу, излучает ФМ-сигнал, и если в приемнике осуществляется частотное детектирование, то после него производится обратная коррекция.

Высокая помехоустойчивость УМ-сигнала при m>>1 имеет «оборотную сторону»: большая эффективная полоса частот П, занимаемая этим сигналом. Поскольку теоретически спектр УМ сигнала бесконечно широкий, при определении П обычно учитываются составляющие спектра с амплитудами не менее 1% амплитуды немодулированного сигнала. При этом эффективная полоса определяется приближенным соотношением:

,

из которого следует, что при m>>1 полоса частот УМ сигнала значительно превосходит полосу частот АМ сигнала (при гармонической модуляции П_АМ = 2F).

Основные характеристики и показатели качества при угловой модуляции, как и при других видах модуляции, определяются статической модуляционной характеристикой (СМХ) (или ), где – постоянное напряжение, подаваемое на вход модулятора (рис. 8.3, а). Эта характеристика должна быть достаточно линейной в пределах требуемых девиаций ( ) и иметь высокую крутизну. Нелинейность СМХ вызывает нелинейные искажения, которые, например, при ЧМ состоят в том, что при модуляции гармоническим сигналом изменение частоты оказывается равным

Коэффициенты нелинейных искажений по 2-й и 3-й гармоникам составляют:

; и т.д.

Динамические модуляционные характеристики: амплитудная (рис. 8.3, б) и частотная (рис. 8.3, в).

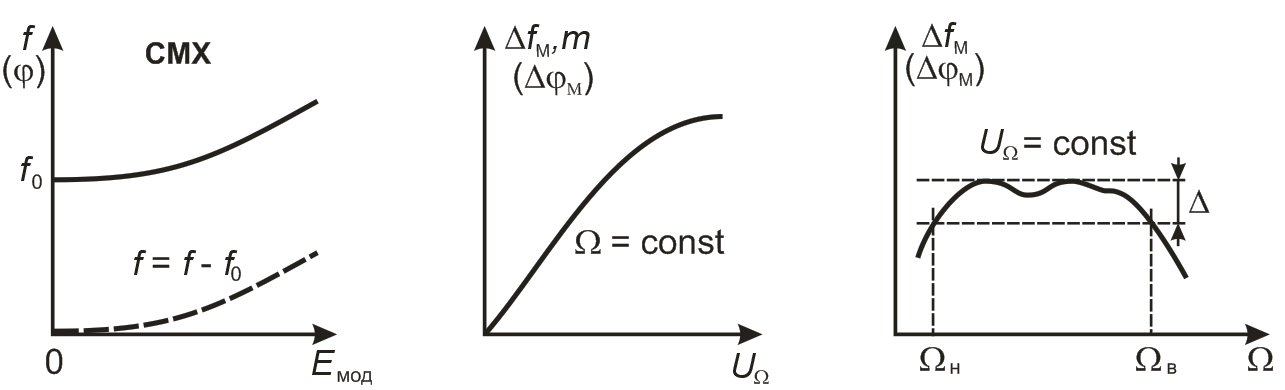
а б в

Рис. 8.3. Основные характеристики при угловой модуляции:

а - статическая модуляционная характеристика (СМХ); б – амплитудная,

в – частотная динамические модуляционные характеристики