
- •А6. Однородная балка, массой 12кг удерживается в равновесии на трехгранной призме при помощи вертикальной силы f . Определите величину силы f , если призма делит балку
- •1 Порция 2 порция
- •1 Состояние 2 состояние
- •М атематическая модель решения.
- •Графическое представление решения.
- •М атематическая модель решения.
- •1 3. Первый конденсатор емкостью 3с подключен к источнику тока с эдс , а второй
- •Графическое представление решения.
- •1.Решение на основе графического моделирования
- •П остроим график движения автомобиля без опоздания со скоростью
- •1.Вариант физического моделирования путем создания графических образов
- •6 .График движения автобуса и легкового автомобиля
- •7. Совместим движение двух видов транспорта согласно условию задачи
- •8. Переведем задачу из физической интерпретации в геометрическую.
- •1 .Вариант физического моделирования путем создания графических образов
- •6 .График движения автобуса и легкового автомобиля
- •7. Совместим движение двух видов транспорта, согласно условию задачи
- •1.Вариант физического моделирования путем создания графических образов
- •1.Решение на основе графического моделирования
- •1.Решение на основе графического моделирования
- •6 .График движения автомобиля и мотоциклиста
Атаманская М.С., Панченко М.Н.
ЕГЭ. Решение физических задач методом графического моделирования.
Учащиеся и учителя испытывают трудности при решении физических задач, с которыми они сталкиваются в материалах итоговой аттестации по физике и математике. Несомненно, они решают задачи с физическим содержанием по-своему. Предлагаем учителям познакомиться с методикой решения текстовых задач физического содержания на основе графического моделирования.
Необходимым условием успешного выполнения физических задач является понимание содержания на основе возможности выбора или разработки учеником физической (графической) модели в удобной знаковой форме.
Решая задачу физического содержания, мы должны представлять тот процесс, который описывается в задаче. Невозможность непосредственного восприятия объектов усложняет ученику задачу, требует реконструкции текста, моделирования условия. Ученику необходимо создать на основе текста модель описываемой ситуации, или графический образ, а затем осуществить логические операции с построенным в воображении представлением. Наиболее эффективный способ понимания условия задачи с физическим содержанием достигается при поэтапном построении сначала пространственно-временной картины изучаемого, а затем – при построении графиков. Только после этого учащиеся могут приступать к математической модели описания.
Решение физических задач требует от учителя большой личностной работы. Не каждый учитель готов к такой деятельности. А может быть он не почувствовал красоту подхода?
Рассмотрим задания, предлагаемые на государственной итоговой аттестации по физике в 2010 году.


![]()

А
![]()


 1.
На графике представлена зависимость
проекции скорости шарика на ось ОХ от
времени. Х- координата возрастает в
интервале времени
1.
На графике представлена зависимость
проекции скорости шарика на ось ОХ от
времени. Х- координата возрастает в
интервале времени
1![]() )
от 0 до 1 с 2) от 0 до 3 с
)
от 0 до 1 с 2) от 0 до 3 с
3
![]()
![]()
![]()
![]()
![]() )
от 0 до 4 с 4) от 3 до 5 с
)
от 0 до 4 с 4) от 3 до 5 с
Графическое представление движения.
|
Математическая модель решения.
Тело движется вдоль оси х в интервале времени от 0 до 4с, так как проекция скорости принимает положительные значения. При движении вдоль оси координата шарика увеличивается. Следовательно, координата х шарика возрастает в интервале времени от 0 до 4 с. Ответ: 3)
|
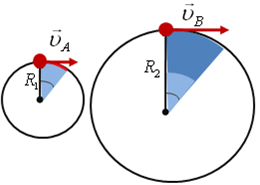
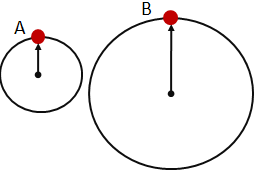
А2. Точка А движется по окружности радиусом 2м, а точка В – по окружности радиусом 4м. Угловые скорости точек одинаковы. Найдите отношение линейной скорости точки А и линейной скорости точки В.
4 2) 1 3) 2 4)

Р
![]() еконструкция
условия задачи.
еконструкция
условия задачи.
![]()
![]()
![]()
![]()
![]()
Шаг 1. Шаг 2. Шаг 3.
Точка А движется по окружности радиусом 2м, а точка В – по окружности радиусом 4м. |
Угловые скорости точек одинаковы |
Найдите отношение линейной скорости точки А и линейной скорости точки В. |
|
Математическая модель решения.
По условию задачи
Ответ: 4) |

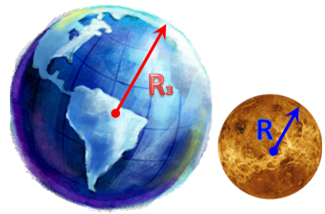
А3. Планета имеет радиус в 2 раза меньший радиуса Земли. Известно, что ускорение свободного падения на этой планете равно 9,8м/с2. Чему равно отношение массы планеты к массе Земли?
Р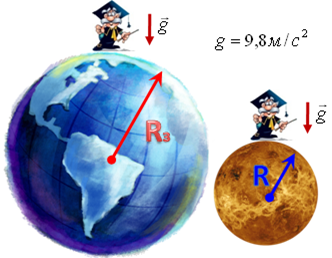 еконструкция
условия задачи.
еконструкция
условия задачи.
![]()
Шаг 1. Шаг 2.
Планета имеет радиус в 2 раза меньший радиуса Земли |
Известно, что ускорение свободного падения на этой планете равно 9,8м/с2. Чему равно отношение массы планеты к массе Земли? |
|
Математическая модель решения По условию Ускорение свободного падения на планете и Земле
П
Ответ: |
Анализ ответа
Рис 1.
Рис 2. |

А4. Чему равна скорость неподвижно лежащего бруска массой 4кг, если в него попадает пуля массой 20г, летящая горизонтально со скоростью 700м/с, и застревает в нем?
Реконструкция условия задачи
![]()
![]()
![]()
![]()
![]()
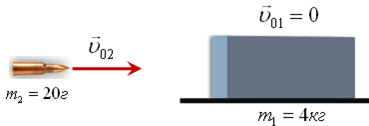
В неподвижно лежащий брусок массой 4кг, попадает пуля массой 20г, летящая горизонтально со скоростью 700м/с |
Чему равна скорость бруска, если пуля застревает в нем?
|
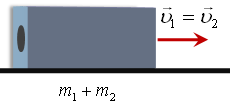
Шаг 1. Шаг 2.
 Дано
Графическое
представление взаимодействия.
Дано
Графическое
представление взаимодействия.

![]()
![]()
![]()

![]()
Рис 1. Рис 2.
![]()

Математическая модель решения.

![]()
По закону сохранения импульса
![]()
![]()
 ОХ:
ОХ:

![]()
Ответ:

А![]() 5.
В цилиндрический сосуд, доверху
наполненный водой, опускают шарик массой
m=0,2кг
и плотностью . Диаметр
шарика меньше диаметра и высоты сосуда.
Определите массу воды, которая выльется
из сосуда.
5.
В цилиндрический сосуд, доверху
наполненный водой, опускают шарик массой
m=0,2кг
и плотностью . Диаметр
шарика меньше диаметра и высоты сосуда.
Определите массу воды, которая выльется
из сосуда.
1) 0,2кг 2) 0,16кг 3) 0,25кг 4) 0,4кг
Реконструкция условия задачи.
![]()
Шаг 1. |
В
. Диаметр шарика меньше диаметра и высоты сосуда. |
Шаг 2. |
Определите массу воды, которая выльется из сосуда.
|
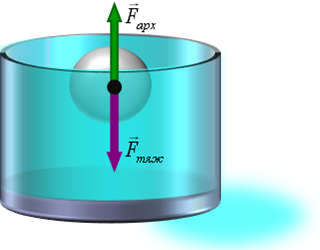
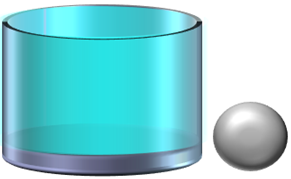
Графическое представление процесса.
![]()
![]()
![]()
Рис 1. Рис 2. Рис 3.
Дано:
|
Математическая модель решения.
Приравняем (1) и (2) Ответ: 1 )
|

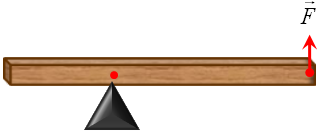
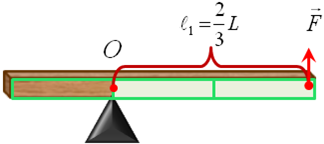
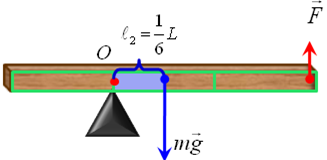
А6. Однородная балка, массой 12кг удерживается в равновесии на трехгранной призме при помощи вертикальной силы f . Определите величину силы f , если призма делит балку
в отношении 2:1
1) 12Н 2) 30Н 3) 60Н 4) 120Н
Реконструкция условия задачи.
![]()
![]()


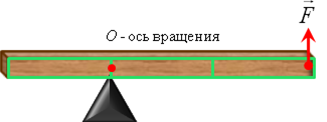
Шаг 1. Шаг 2.
Однородная балка, массой 12кг удерживается в равновесии на трехгранной призме при помощи вертикальной силы F . |
Определите величину силы F , если призма делит балку в отношении 2:1
|
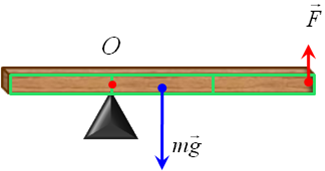 Дано:
Графическое
представление решения.
Дано:
Графическое
представление решения.
![]()

![]()

![]()
-
Покажем на рисунке силы, действующие на балку.
Рис 1.
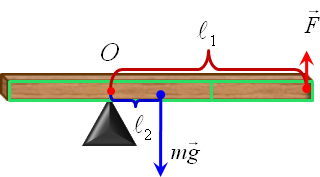
Сопоставим силы и плечи: плечо силы
 ,
плечо силы
,
плечо силы
 .
.Рис 2.
-
О
 бозначим:
L
– длина балки, тогда
бозначим:
L
– длина балки, тогдаРис 3.

Рис 4.
Математическая модель решения.
![]()
![]()
 По
условию равновесия рычага
По
условию равновесия рычага
![]() .
Силы
.
Силы
 Обозначим:
Плечи
сил
Обозначим:
Плечи
сил
![]()
![]()
![]()

Ответ: 2 )

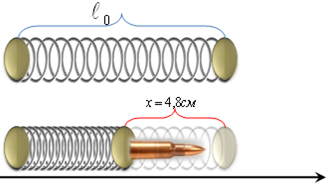
А7. Для выстрела из пружинного пистолета его пружину жесткостью 5,2кН/м сжимают на 4,8см. Какова будет скорость снаряда массой 97г при горизонтальном выстреле?
 Реконструкция условия
задачи.
Реконструкция условия
задачи.
Для выстрела из пружинного пистолета его пружину жесткостью 5,2кН/м сжимают на 4,8см. Шаг 1. |
Какова будет скорость снаряда массой 97г при горизонтальном выстреле? Шаг 2.
|
Дано: Графическое представление процесса.
Положение 1.
![]()
![]()

![]()
![]()
![]()
![]()
Пружина сжата, следовательно она обладает потенциальной энергией.
![]() Рис
1.
Рис
1.

![]()
![]()
 Положение
2.
Положение
2.
![]()
Пружина вернулась в первоначальное положение.
Рис 2.
Математическая модель решения.
![]()
 По
закону сохранения механической энергии
По
закону сохранения механической энергии
![]()
![]()
![]()

![]()

Выразим скорость
![]()
Ответ:
А 1) 1 2) 2 3) 3 4) 4
Графическое представление модели газа. Д
|
|
![]()
![]()
N- число молекул, V-объем m – масса, V-объем
Концентрация – это число молекул в единице объема. Рис 1. |
Плотность – это масса вещества в единице объема. Рис 2. |
Математическая модель решения.
![]()
К
![]()
 онцентрация
молекул
онцентрация
молекул
![]()


 Плотность
газа
Плотность
газа
Формула устанавливает прямо пропорциональную зависимость между
плотностью газа и концентрацией молекул (график №3)
Ответ: 3)


А9. В сосуде, закрытом поршнем, находится идеальный газ. График зависимости давления газа от температуры при изменении его состояния представлен на рисунке. Какому состоянию газа соответствует наибольшее значение объема? 1) 1 2) 2 3) 3 4) 4
Графическое представление изохорного процесса. Т.к. график устанавливает зависимость давления p от температуры T, то необходимо вспомнить изохорный процесс.
|
|
|||
П
Рис 1 |
Проведем две изохоры, соответствующие разным объемам
Рис 2. |
Проведем
прямую, соответствующую фиксированной
температуре, которая пересечет графики
в точках
Рис 3. |
||
Анализ графиков показывает, что изохора, соответствующая большему объему, лежит ниже. Вернемся к графическому представлению условия задачи.
|
||||
Рис 4. |
Проведем изохоры через точки А,В,С,D.
Изохора ОD соответствует большему объему, наибольшему значению объема соответствует точка D.
Ответ: 4) |
|||

А10. В
теплоизолированном сосуде смешивают
водород количеством вещества 1 моль со
средней кинетической энергией молекул
![]() и кислород количеством вещества 4 моль
со средней кинетической энергией молекул
и кислород количеством вещества 4 моль
со средней кинетической энергией молекул
![]() .
Чему будет равна средняя кинетическая
энергия молекул после смешивания?
.
Чему будет равна средняя кинетическая
энергия молекул после смешивания?
 1)
1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]()
![]()
 Реконструкция
условия задачи.
Реконструкция
условия задачи.
![]()
![]()


![]()
![]()












 Дано:
Дано:


 Дано:
Дано:






 риравняем
(1) и (2)
риравняем
(1) и (2)


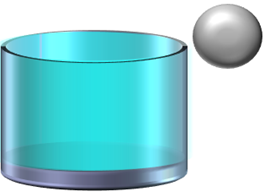
 цилиндрический сосуд, доверху
наполненный водой, опускают шарик
массой m=0,2кг
и плотностью
цилиндрический сосуд, доверху
наполненный водой, опускают шарик
массой m=0,2кг
и плотностью












 8.
Какой из графиков отражает связь
между плотностью газа и концентрацией
его молекул
8.
Какой из графиков отражает связь
между плотностью газа и концентрацией
его молекул ля
ответа на вопрос задачи необходимо
вспомнить понятие концентрации и
плотности.
ля
ответа на вопрос задачи необходимо
вспомнить понятие концентрации и
плотности.























