Лабораторная работа № 8 Изучение алгоритма цифровой свертки

Цель работы

1. Изучение алгоритмов цифровой свертки.

2. Изучение функций Matlab, позволяющих автоматизировать процесс вычисления цифровой свертки.

3. Получение навыков расчета низкочастотных фильтров с использованием алгоритмов цифровой свертки.

Теоретическое обоснование

При цифровой обработке сигналов широко используется понятие линейной системы. Процессы в линейных системах описываются линейными уравнениями, что позволяет использовать математические модели линейных систем в более широких областях техники по сравнению с математическими моделями нелинейных систем.

Модель системы может быть задана с помощью следующих подходов:

– систему задают как «черный ящик», внутреннее устройство которого неизвестно, а известны только сигналы на входе x(t) и выходе y(t) системы;

– задают структуру системы, детально описывают все блоки, входящие в структуру, и их соединения.

Далее, для создания модели использован первый подход. В теории систем вместо термина преобразования сигналов, применяемого в технике, используется термин «оператор». В линейных системах осуществляется линейное преобразование сигналов, которому в математике ставится в соответствии линейный оператор G, для которого y(t) = Gx(t).

Оператор G называется аддитивным, если G(x₁(t) + x₂(t)) = Gx₁(t) + Gx₂(t),

и однородным, если G(x(t)) = Gx(t), где  – любое число.

Линейными называются такие системы, операторы которых аддитивны и однородны. Наличие свойств аддитивности и однородности определяет принцип суперпозиции (наложения), в соответствии с которым сложный входной сигнал можно представить как последовательность простых сигналов и для каждого простого сигнала можно найти выходной сигнал. Тогда, согласно принципу суперпозиции, реакция системы на сложный входной сигнал может быть найдена как сумма реакций на составляющие входного сигнала.

Инвариантными во времени (или стационарными) называются такие системы, которые одинаковым образом преобразуют сигналы, отличающиеся лишь временем их прихода, оператор которых обладает свойством: если y(t) = Gx(t), то для любого сдвига  будет справедливо y(t – ) = Gx(t – ).

Если вход и выход системы являются непрерывными, то такие системы называются аналоговыми; если сигналы на входе и выходе квантуются по времени, то системы называются дискретными; если сигналы на входе и выходе квантуются по времени и уровню, то системы называются цифровыми. На первом этапе исследования системы квантование по уровню не учитывают, что позволяет исследовать цифровые системы как дискретные. Результат такого рассмотрения является ориентировочным, требующим уточнения. Например, система, рассчитанная как дискретная, может удовлетворять поставленным требованиям, а расчеты той же системы с учетом квантования по уровню могут показать, что система неработоспособна.

Любой непрерывный сигнал можно представить в виде разложения по единичным импульсам как

. (8.1)

Единичный импульс или δ(t) – функция, определяемая как

(8.2)

где

.

Выражение (8.2) определяет короткий импульс бесконечно малой длительности и бесконечно большой амплитудой с площадью, равной единице.

При подаче на вход системы импульса δ(t) на выходе получим импульсную переходную характеристику w(t).

Основываясь на принципе суперпозиции, вычисление отклика системы на сигнал сложной формы можно свести к простой схеме: разложить сложный сигнал на составляющие и вычислить выходной сигнал как сумму откликов на все составляющие входного сигнала. Каждый из единичных импульсов входного сигнала x(t) вызывает на выходе системы отклик, состоящий из откликов h(t), но имеющий амплитудный множитель x()d и запаздывание , то есть x()h(t – )d. Так как выходной сигнал является суммой всех элементарных откликов, то

. (8.3)

Это соотношение называется интегралом Дюамеля или интегралом свертки, y(t) является сверткой функций x(t) и h(t), что обозначается *.

Интеграл Дюамеля является моделью аналоговой инвариантной линейной системы. Математические функции x(t) и h(t) равноценны и подстановкой можно получить новую форму интеграла свёртки

. (8.4)

Подадим на вход дискретной системы дискретный сигнал в виде единичного импульса (nT_П)

где n – натуральный ряд чисел 0, 1, …, n; Т_П – интервал дискретности.

Точно так же, как и для непрерывных сигналов, произвольную дискретную последовательность можно записать в виде суммы:

, (8.5)

где n и k – номера чисел в последовательности; x_Д(nT_П) – дискретный сигнал.

Обозначим через w(nT_П) отклик системы на единичный дискретный импульс (nT_П). Тогда отклик системы на сложный дискретный сигнал

. (8.6)

Таким образом, любая инвариантная линейная дискретная система полностью характеризуется импульсной характеристикой w(nT_П), которая представляет некоторую дискретную последовательность. Последнее выражение носит название цифровой свёртки. Заменив в ней переменную можно получить другое выражение:

. (8.7)

Из выражений (8.6) и (8.7) видно, что порядок переменных в свертке не важен. Иными словами, линейная система с дискретным входом x(nT_П) и дискретной переходной характеристикой h(nT_П) будет иметь тот же выход, что и линейная система с дискретным входом h(nT_П) и дискретной переходной характеристикой x(nT_П).

Ввиду исключительной важности интеграла свертки рассмотрим еще один метод получения выходной последовательности, которым удобно пользоваться, когда входной и выходной сигналы системы заданы графически. С введением интервала дискретности непрерывные функции можно представить последовательностью равноотстоящих импульсов.

x(t) = a₀(t) + a₁(t – Т_П) + a₂(t – 2Т_П) + a₃(t – 3Т_П) +…

h(t) = b₀(t) + b₁(t – Т_П) + b₂(t – 2Т_П) + b₃(t – 3Т_П) +…

Изображения этих функций представлены ниже:

X(z) = a₀ + a₁z^-1 + a₂z^-2 + a₃z^-3 +… (8.8)

H(z) = b₀ + b₁z^-1 + b₂z^-2 + b₃z^-3 +… (8.9)

С учетом (8.7) – (8.9) выходной сигнал

Y(nT_П) = L^-1[X(z)H(z)] = L^-1[a₀b₀ + (a₀b₁ + a₁b₀)z^-1 + (a₀b₂ + a₁b₁ + a₂b₀)z^-2 + …] =

= [a₀b₀(t) + (a₀b₁ + a₁b₀)(t – Т_П) + (a₀b₂ + a₁b₁ + a₂b₀)(t – 2Т_П) + …]. (8.10)

Следовательно, для определения свертки двух дискретных последовательностей необходимо их перемножить, а затем сгруппировать члены при одинаковых степенях z. В пакете Matlab дискретная свертка вычисляется с помощью функции conv

z=conv(x,h).

Описание работы

Вычислим дискретную свертку при условии, что дискретный входной сигнал x(nT_П) и дискретная переходная характеристика системы h(nT_П) заданы последовательностями отсчетов функций

x=[1 3 2];

h=[1 2 3 4];

y=conv(x,h)

y= 1 5 11 17 18 8.

Эту же последовательность можно получить, используя выражения (8.6) и (8.7). Первый импульс входной последовательности x_Д(nT_П) вызовет отклик

1 2 3 4.

Второй импульс входной последовательности x_Д(nT_П) спустя вызовет отклик

3 6 9 12.

Третий импульс через 2 вызовет следующую последовательность:

2 4 6 8.

Суммируя последовательности с учетом временного сдвига получим:

1 2 3 4

3 6 9 12

2 4 6 8

1 5 11 17 18 8

Этот результат соответствует результату, полученному в пакете Matlab функцией conv. Этот результат можно получить согласно (8.10).

Интеграл свертки осуществляет сглаживание входных сигналов и поэтому может быть использован для проектирования низкочастотных фильтров. В этом случае задают весовые коэффициенты функции w(nT_П). В пакете Matlab дискретная фильтрация выполняется командой filter:

y=filter(b,a,x);

где b – вектор нерекурсивной части фильтра (числителя функции передачи); а – вектор коэффициентов рекурсивной части фильтра (знаменателя функции передачи), х – входной сигнал. Возвращаемой величиной является вектор отсчетов входного сигнала фильтра.

Между функциями filter и conv существуют два различия. Во-первых, функция conv требует задания импульсной характеристики фильтра в виде вектора. Поэтому импульсная характеристика должна иметь конечную длину. Фактически это означает, что с помощью функции conv можно реализовать только нерекурсивные фильтры. С помощью функции filter можно реализовать и рекурсивные фильтры, т.е. фильтры с бесконечной импульсной характеристикой. Во-вторых, функция filter возвращает результат, длина которого равна длине входного сигнала.

Повторим пример по расчету фильтра, используя функцию filter. Поскольку используется импульсная характеристика фильтра, то в передаточной функции фильтра (команда filter) в качестве коэффициента в нерекурсивной части фильтра должна быть задана его импульсная характеристика (вектор h), а в рекурсивной части фильтра вектор а должен быть представлен скаляром, равным единице:

z= filter(h,1,x)

z=1 5 11.

Видно, что результат фильтрации совпадает в трех первых пунктах со значениями, полученным с помощью функции conv. Если бы входной сигнал х имел четыре отсчета, то совпадение наблюдалось бы в четырех точках, то есть вектор z не содержит затухающих «хвостов». Различия в вычислениях объясняется тем, что функция conv предполагает завершенность входного сигнала, а функция filter завершенность входного сигнала не требует и позволяет, при необходимости, продолжать обработку поступающих на вход фильтра новых отсчетов.

Чтобы получить результат, совпадающий с результатом функции conv, входной вектор х нужно дополнить необходимым количеством нулей:

z1=filter(h,1,[x,0,0,0])

z1=1 5 11 17 18 8.

При фильтрации сигналов в ряде случаев возникает необходимость сохранения фазовых соотношений в исходном сигнале. Для этого требуется фильтр с линейной ФЧХ или иначе с постоянной фазовой задержкой. Это достигается в нерекурсивных фильтрах с симметричным набором коэффициентов b_i = b_m-i, которые определяются конечной импульсной характеристикой. Нерекурсивные фильтры обладают бесконечной импульсной характеристикой и поэтому принципиально не могут иметь линейную ФЧХ.

Для реализации фильтрации с нулевым фазовым сдвигом в Matlab раз-работана функция filtfilt. Ее название символизирует смысл выполняющих ею действий: сначала входной сигнал фильтруется как обычно, а затем производится второй проход фильтрации, при котором сигнал обрабатывается от конца к началу. Если заданный фильтр характеризуется передаточной функцией W( ), импульсной характеристикой h(nT_П) и АЧХ – W(ω), то фильтр, эквивалентный двум проходам обрабатываемого сигнала (прямой и обратный проход), будет характеризоваться передаточной функцией W(z)W(z^-1), АЧХ |W(ω)|² и нулевой ФЧХ. Импульсная характеристика фильтра с нулевым фазовым сдвигом представляет собой корреляционную функцию исходной импульсной характеристики:

,

Синтаксис вызова функции filtfilt:

y=filtfilt(b,a,x).

Приведем пример, демонстрирующий компенсацию фазового сдвига с помощью функции filtfilt. Создадим сигнал в виде прямоугольного импульса, дополненного с обеих сторон нулями:

S=[zeros(50,1);ones(100,1);zeros(50,1)].

В качестве фильтра используем ФНЧ Чебышева первого рода с достаточно сильными пульсациями АЧХ в полосе пропускания (3 дБ) и низкой частотой среза (0,05 частоты Найквиста), чтобы выходной импульс был заметно искажен [b,a]=cheby1(7,5,0,05).

Обработайте сигнал с помощью filter и filtfilt и постройте графики входного и выходного сигналов

s=[zeros(50,1);ones(100,1);zeros(50,1)]; %Входной сигнал

[b,a]=cheby1(7,5,0.05); %Коэффициенты фильтра Чебышева

s1=filter(b,a,s); %Результат фильтрации

s2=filtfilt(b,a,s); %Результат фильтрации

plot(s)

hold on

plot(s1,'--'),grid on %Графики выходных сигналов

plot(s2,'-.'),grid on %Графики выходных сигналов

hold on.

Результат представлен на рис. 8.1.

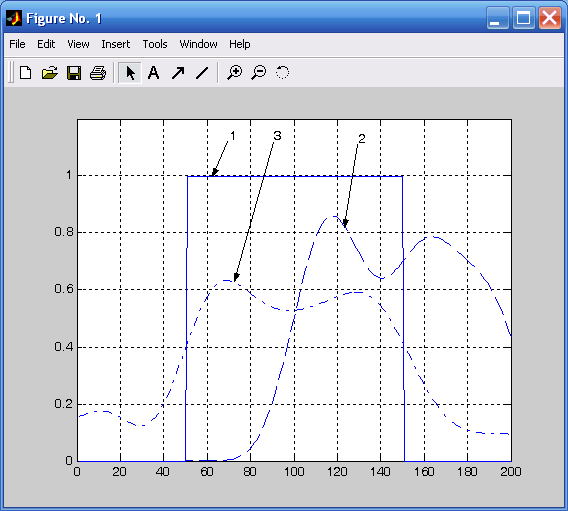
Рис. 8.1. График сигналов:

1 – входной сигнал, 2 – преобразованный сигнал (обычная фильтрация);

3 – преобразованный сигнал (фильтрация с компенсацией фазового сдвига)

Интеграл свертки используется при проектировании цифровых фильтров. Для этого требуется задать весовые коэффициенты или, что одно и то же, импульсную характеристику, которую можно получить путем подачи на вход фильтра единичного сигнала, дополненного некоторым количеством нулей filter(b,a,[1,zeros(1,N)]).

По известным коэффициентам передаточных функций коэффициенты импульсной характеристики определяются как n=impz(b,a,n), где b, a – по-линомы числителя и знаменателя; n – вектор отсчетов импульсной характе-ристики. Если он не указан, то Matlab автоматически выбирает число отсче-тов в зависимости от поведения импульсной характеристики. На рис. 8.2 представлена импульсная характеристика для фильтра Баттерворта пятого порядка.

[b,a]=butter(4,0.2); %Фильтр Баттерворта пятого порядка

%с частотой среза 0.2