Лабораторная работа № 7 Идентификация объектов по кривым разгона

Цель работы

1. Изучение методики идентификации объектов по кривым разгона.

2. Изучение возможности и области применения метода моментов при идентификации объекта по кривым разгона.

Теоретическое обоснование

При идентификации объекта определяют коэффициенты дифференциальных уравнений, описывающих его, или передаточные функции. Для этой цели предложено несколько методов, из которых метод площадей в инженерной практике наиболее распространён.

Однако этот метод имеет существенные недостатки:

– повышенные требования к точности вычисления площадей, так как ошибки в определении площадей низкого порядка накапливаются при последующих вычислениях;

– повышенные требования к определению времени запаздывания, которое, во-первых, трудно фиксируется на фоне промышленных помех, во-вторых, носит случайный характер.

В данной работе исследуются два алгоритма идентификации объекта по кривым разгона. Для первого алгоритма следует определить два момента и задать начальные условия (начало рабочего участка и скорость выходной величины в начале рабочего участка). Для второго алгоритма начальные условия не задаются, но требуется определить четыре момента.

Пусть объект описывается линейным дифференциальным уравнением

, (7.1)

где, – выходные и входные сигналы.

При t = 0 подадим на вход ступенчатое воздействие и к входному и выходному сигналу исследуемого объекта применим оператор

. (7.2)

После преобразования получим

, (7.3)

где α_k = Y^k(τ), k = 0, 1, …, n. Величина τ выбирается таким образом, чтобы исключить неконтролируемое время запаздывания.

Применим преобразование (7.2) к выражению (1 – Y(t)):

. (7.4)

Подставляя в (7.4) значение L{Y(t)} после преобразования получим

. (7.5)

Соотношение (7.5) с учетом (7.2) записывается в следующем виде:

. (7.6)

Ограничимся системой второго порядка, разложив функции e^-st и e^-sτ в ряд Тейлора:

(7.7)

где α₀, α₁ – значение Y(t) и её производной при t = τ, а переменные β₁, β₂, …, β_n выражены через соответствующие интегралы:

(7.8)

Приравнивая коэффициенты выражения (7.7) при одинаковых степенях s, получим систему уравнений

(7.9)

Решая первые два уравнения системы (7.9) можно выразить коэффициенты передаточной функции a₁ и a₂ через интегралы ₁ и ₂, начальные условия ₀(τ), ₁(τ) и время достижения выходной величины системы τ рабочей точки

(7.10)

Исключая из системы (7.9) ₀ и ₁ получаем выражения для вычисления коэффициентов a₁ и a₂ через ₁, ₂, ₃, ₄ и τ. Этим методом целесообразно пользоваться тогда, когда выходной сигнал искажен действиями помех и определение начальных условий, особенно производных, представляет известные трудности.

Выражение для определения коэффициентов передаточной функции упрощается, если оператор (7.2) представить в виде

, (7.11)

где t – время включения интеграторов при t = τ.

Отсчет времени в операторах (7.2) и (7.11) разный: в операторе (7.2) время отсчитывается от момента подачи на систему воздействия, а в операторе (7.11) время отсчитывается при достижении выходной величины рабочей точки. С учетом этого замечания, между операторами (7.2) и (7.11) устанавливается следующее соотношение:

, (7.12)

где t = t + τ.

Применив оператор (7.11) к выражению (7.7) получим, что выражение для определения коэффициентов передаточных функций упрощается, в нем исчезает сомножитель e^-sτ

(7.13)

Приравнивая члены при одинаковых степенях s, получим

(7.14)

Из (7.14) можно определить а₁ и a₂.

(7.15)

Для выражения коэффициентов а₁ и a₂ по выражению (7.15) необходимо знать значения выходной величины и её производную при t = τ.

Если вычисление начальных условий затруднительно, то для определения а₁ и a₂ следует воспользоваться системой (7.14)

(7.16)

Описание работы

Реализация блока идентификации по выражению (7.15) представлена на рис. 7.1. Подсистема 1 (Subsystem1) маскирует исследуемый объект. Подсистема 2 (Subsystem2) формируются стробирующие сигналы, по которым запускаются интеграторы и начинается процесс определения коэффициентов а₁ и а₂.

Рис. 7.1. Функциональная схема устройства для определения коэффициентов а₁ и а₂ (7.15)

Принципиальная схема Subsystem2 представлена на рис. 7.2. Она имеет два входа (In1 и In2) и три выхода (Out1, Out2 и Out3). На вход In1 подается сигнал, определяемый выражением (1 – y(t)), а на вход In2 подается сигнал, определяющий начало рабочего участка. На выходах Out1 и Out2 формируются стробирующие сигналы, по которым запускаются интеграторы и начинается процесс обработки кривой разгона. На выходе Out3 появляется сигнал, определяющий ₂, а на выходе интегратора (Integrator) появляется сигнал, определяющий ₁. Блок Relational Operator формирует стробирующие сигналы. Сигнал задания на входе In2 перемещает стробирующие сигналы по всей кривой разгона. Блок Dot Product определяет подынтегральное выражение интеграла ₂.

Подсистема (Subsystem3) (рис. 7.3) реализует преобразования, входящие в выражение (7.15), и определяет коэффициенты и . С помощью блока Sample and Hold определяются начальные условия для выходной величины (коэффициент ), а с помощью блока Sample and Hold1 – для производной выходной величины (коэффициент ). Сумматор Sum и блоки умножения Product реализуют выражение (7.15). Результат вычислений представлен на соответствующих дисплеях (выход Out1 и Out2).

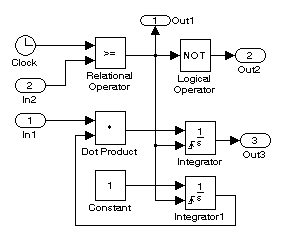
Рис. 7.2. Принципиальная схема Subsystem2

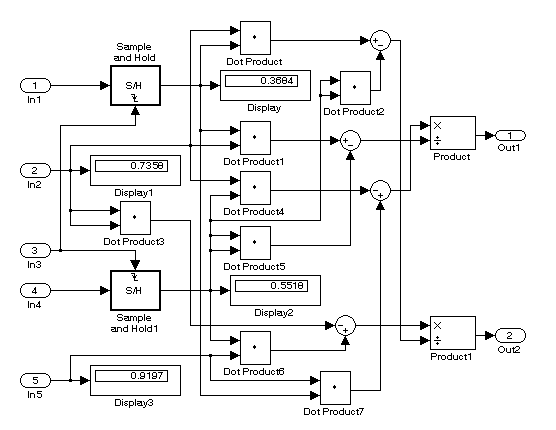
Рис. 7.3. Принципиальная схема Subsystem3

Принципиальная схема устройства для определения коэффициентов и по выражениям (7.15) и (7.16) представлена на рис. 7.4. Причем подсистема (Subsystem) определяет коэффициенты в соответствии с выражением (7.15), а остальные блоки Simulink определяют коэффициенты и по выражению (7.16).

Для формирования функций времени, соответствующих подынтегральным выражениям (7.8), применен ряд последовательно соединенных интеграторов с масштабными множителями. Для определения β₂ ступенчатое единичное воздействие необходимо проинтегрировать дважды и умножить на 2, а для определения β₃ – интегрировать трижды и умножить на 6.

Рис. 7.4. Принципиальная схема устройства определения коэффициентов

дифференциальных уравнений

Результаты исследования системы второго порядка представлены на регистрирующих блоках (Display1 – Display4). Исключение начального участка кривой разгона задается константой блока Constant. Если корни характеристического уравнения передаточной функции объекта значительно отличаются по абсолютной величине, то увеличение времени запаздывания понижает точность определения коэффициентов передаточной функции вторым методом. Это объясняется тем, что составляющие переходного процесса, характеризующиеся большими по абсолютной величине корнями, появляются в начальной стадии кривой разгона. Увеличение запаздывания может уменьшить зону действия больших по абсолютной величине корней, поэтому точность определения коэффициентов а₁ и а₂ будет уменьшаться. В исследуемом примере объект характеризуется двумя корнями р₁ = –1; р₂ = –2. При τ = 0,5 с ошибка в определении коэффициента а₁ вторым методом составила 0,5 %, а ошибка в определении а₂ составила 1,1 %. При τ = 3 с ошибка в определении коэффициентов возросла и составила для а₁ 1,7 %, а для а₂ – 5 %.

Постоянная, вносимая в блок Constant, должна выбираться из двух противоположных положений: с одной стороны, она должна быть достаточно большой, чтобы перекрыть неконтролируемое запаздывание, а с другой стороны, достаточно малой, чтобы не была утеряна составляющая переходного процесса, определяемая большими по абсолютной величине корнями.

Задание

1. Рассчитать параметры структурных схем.

2. Для индивидуального задания составить структурную схему устройства для определения коэффициентов передаточных функций на участке кривой разгона с учетом начальных условий.

3. Определить параметры передаточной функции.

4. По рассчитанным параметрам составить структурную схему устройства для определения коэффициентов передаточных функций на участке кривой разгона без учета начальных условий с помощью увеличенного количества моментов.

5.Определить параметры передаточной функции.

6.Оценить корректность методик, внося возмущения в функционирования алгоритма путем ввода погрешностей в структурную схему.

Содержание отчета

1. Структурные схемы различных устройств для определения коэффициентов передаточных функций.

2. Найденные коэффициенты передаточных функций.

Контрольные вопросы

1. На каких математических преобразованиях базируется методика определения коэффициентов передаточных функций на участках кривой разгона?

2. Обоснуйте структурную схему устройства, позволяющую определять коэффициенты передаточных функций на участке кривой разгона для объекта первого порядка с вводом начальных условий.

3. Обоснуйте структурную схему устройства, позволяющую определять коэффициенты передаточных функций на участке кривой разгона для объекта второго порядка с вводом начальных условий.

4. Обоснуйте структурную схему устройства, позволяющую определять коэффициенты передаточных функций на участке кривой разгона для объекта второго порядка с использованием четырех моментов.

5. Почему метод моментов чувствителен к ошибкам задания исходных данных?

6. Какие условия заданы параметром τ?

7. В каких случаях целесообразно использовать вышеприведенные методы идентификации?