1 ‑ Дискретный ( c2d); 2 ‑ дискретный (билинейное преобразование); 3 ‑ аналоговый
Задание
По заданной передаточной функции аналогового фильтра определить передаточные функции дискретных фильтров аналитическим путем при разных интервалах дискретности и при различных методах аппроксимации:
– аппроксимация Эйлера;
– метод инвариантного преобразования импульсной переходной функции;
– метод билинейного преобразования.
Содержание отчета
1. Краткая характеристика используемых в лабораторной работе методик перехода от непрерывных передаточных функций к дискретным передаточным функциям.
2. Листинги программ по расчету дискретных фильтров по их аналоговому эквиваленту.
3. Логарифмические характеристики аналоговых и дискретных фильтров.
4. Анализ результатов расчета аналоговых и дискретных фильтров.
Контрольные вопросы
1. Как перейти от аналогового фильтра к дискретному фильтру, используя аппроксимацию Эйлера?
2. Как перейти от аналогового фильтра к дискретному фильтру, используя метод импульсной переходной характеристики?
3. Как перейти от аналогового фильтра к дискретному фильтру, используя метод билинейного преобразования?
4. Из каких соображений следует выбирать частоту дискретизации при использовании аппроксимации Эйлера?
5. В каком диапазоне изменяется цифровая частота при построении логарифмических характеристик дискретных фильтров?
6. Как по цифровой частоте и интервалу дискретности определить круговую частоту?
7. Запишите выражение, связывающее точки мнимой оси плоскости W с точками мнимой оси плоскости S.
8. Из каких соображений выбирается граничная частота и как она связана с интервалом дискретности?
Лабораторная работа № 6 Расчет цифровых фильтров с учетом квантования
Цель работы
1. Изучение возможностей проектирования цифровых фильтров с помощью пакета FDAtool из библиотеки Filter Desing.
2. Получение навыков проектирования цифровых фильтров.
3. Изучение характеристик цифровых фильтров с учетом квантования по уровню.
Теоретическое обоснование
Для создания дискретных фильтров в Matlab используют пакет FDAtool.
Главное окно программы FDAtool из библиотеки Filter Desing & Analysis Tool показано на рис. 6.1. Оно появляется на экране после загрузки программы, вызываемой набранным именем fdatool.
Главное окно включает несколько областей для ввода и вывода необходимой информации. Рассмотрим эти области в последовательности, которая применяется при разработке фильтра. Прежде всего, разработчик должен сделать выбор между фильтрами с бесконечными и конечными импульсными характеристиками (IIR или FIR), который подтверждается соответствующим флажком в области Design Method. При активном окне FIR можно вызвать ниспадающими меню, которое предлагает несколько вариантов проектирования фильтров. По умолчанию программа предлагает фильтр Eguiripple (фильтр с равномерными пульсациями). При активизации подменю Design Method/FIR/Window Matlab дает возможность осуществлять проектирование фильтров с помощью окон (Window). По умолчанию программа FDAtool предлагает окно Кайзер (Kaiser).
После того, как выбран тип импульсной характеристики фильтра и метод его проектирования, задаём тип фильтра – область Filter Type.
FDAtool предлагает следующие типы фильтров:
‑ Low pass (низких частот);
‑ High pass (высоких частот);
‑ Band pass (полосовой фильтр);
‑ Band stop (режекторный фильтр).
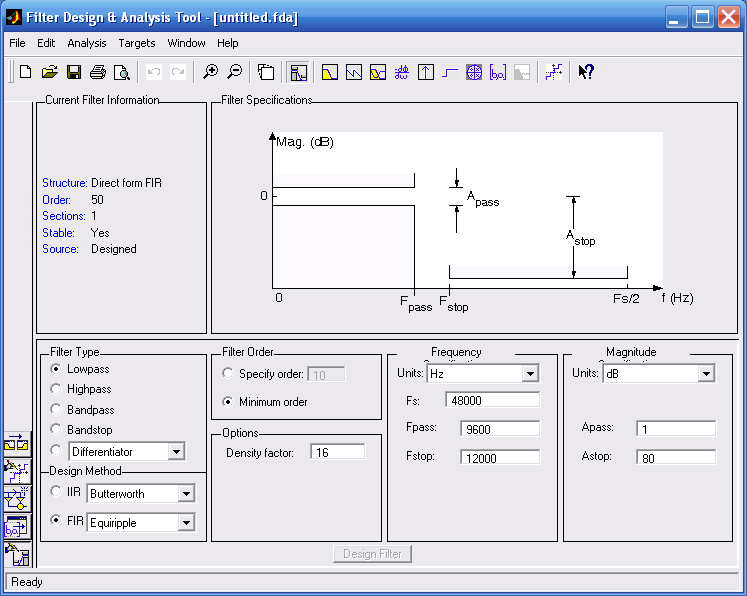
Рис. 6.1. Главное окно программы fdatool
Область Filter type имеет ниспадающее меню, в котором расположены специализированные цифровые фильтры:
‑ Differentiator (дифференциатор);
‑ Hilbert Transformer (преобразователи Гильберта);
‑ Multiband (многополосный фильтр) и т.д.
При выборе типа фильтра, например Band pass, в области Filter Specification появляется поле, в котором представляем основные характеристики фильтра. В правом нижнем углу расположены области Frequency Specification и Magnitude Specification (частотные и амплитудные спецификации соответственно). Первая из них содержит редактируемые окна для ввода значений частоты дискретизации FS, граничных частот полос задерживания (FSTOP1 и FSTOP2) и граничных частот полос пропускания (FPASS1 и FPASS2), а также единицы измерения частоты (Units) при построении АЧХ. Количество граничных частот зависит от типа фильтра, задаваемого в разделе Filter Type. Вторая область – Magnitude Specifications – позволяет задать единицы измерения амплитуды (Units) и ограничений амплитудной характеристики проектируемого фильтра для области пропускания (APASS или ωPASS) и задерживания (ASTOP или ωSTOP).
Приведённые данные позволяют задать АЧХ в функции частоты, изменяющейся от 0 до FS/2 = FН (FН – частота Найквиста).
На странице Design Filter имеется еще одна область – Filter Order (порядок фильтра), в которой можно либо явно задать порядок фильтра либо потребовать, чтобы программа автоматически выбрала наименьший порядок в соответствии с введенными характеристиками фильтра.
Описание работы
Спроектируем полосовой фильтр, параметры которого представлены на рис. 6.2. В поле Filter Specifications заданы контуры АЧХ проектируемого фильтра, а в поле Frequency Specifications и Magnitude Specifications требования к фильтру принимают конкретный вид, заданный соответствующими цифрами. Например, из полей Frequency Specifications и Magnitude Specifications следует, что первая полоса задерживания простирается от 0 до 7200 Гц при ослаблении –80 дБ, а вторая полоса задерживания простирается от 12800 Гц до 24000 Гц при ослаблении –80 дБ.
Теперь, когда заданы все характеристики фильтра, можно приступить к его проектированию (Design Filter). В результате выполнения программы в окне Magnitude Response появится АЧХ проектируемого фильтра (рис. 6.3).
В области «Текущая информация» (Current Filter) отображаются данные, характеризующие проектируемый фильтр (форма представления фильтра, порядок, источник проектирования). В меню Edit имеется подменю Convert Structure (выбор структуры), вход в которое позволяет рассмотреть различные формы реализации фильтров. Появляющаяся информация не позволяет изменить структуру проектируемого фильтра, которая для FIR-фильтров всегда остается неизменной – прямой формы (Direct form FIR). Выпадающий список подменю Convert Structure следует интерпретировать как подсказку пользователю, которая указывает, что кроме проектируемой формы фильтра существуют и другие формы.
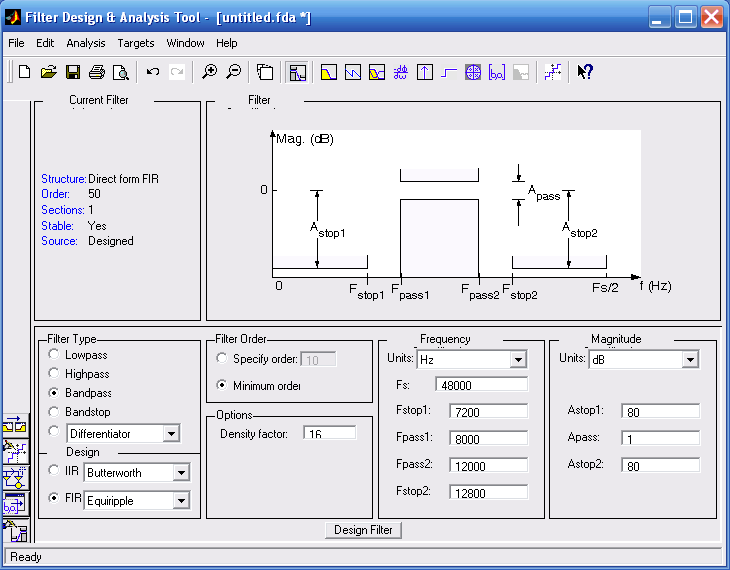
Рис. 6.2. Параметр проектирующего фильтра, заданные в полях окна программы fdatool
Меню Analysis позволяет рассмотреть характеристики фильтра:
‑ Filter Specifications (спецификация фильтра);
‑ Magnitude Response (амплитудно-частотная характеристика);
‑ Phase Response (фазочастотная характеристика);
‑ Magnitude and Phase Response (AЧX, ФЧХ);
‑ Group Delay (групповое время задержки);
‑ Impulse Response (импульсная характеристика);
‑ Step Response (переходная характеристика);
‑ Pole/Zero Plot (полюса и нули);
‑ Filter Coefficients (коэффициенты фильтра).
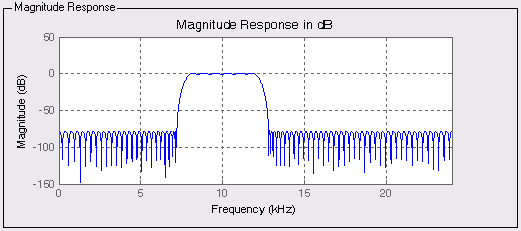
Рис. 6.3. АЧХ проектируемого фильтра
Для отображения характеристики фильтра необходимо выбрать соответствующую команду или нажать одну из кнопок, расположенных под строкой меню. Изменяя тип окна и параметры фильтра можно создавать виртуальные модели различных фильтров и исследовать их характеристики.
В меню, расположенном внизу слева от главного окна, находится кнопка «Реализация модели» (Realize model), нажатие на которую приводит к переходу в окно Realize model, в котором создаются mdl-файлы проектируемых фильтров.
В левой части главного окна находится кнопка Set Quantization Parameters. В главном окне появится новое поле, содержащее надпись Turn Quantization On (возвращение к квантованным коэффициентам). Для запуска процедуры расчета фильтра с квантованными коэффициентами установим в соответствующее поле флажок, запустив тем самым расчет квантованного фильтра с параметрами квантования, заданными его умолчанию.
После окончания процедуры расчета график квантованного фильтра наложится на AЧX фильтра-прототипа (рис. 6.4), АЧХ представленных фильтров имеют незначительные отличия, что характерно для цифровых фильтров с конечной импульсной характеристикой (FIR-фильтров).
Используя исходные данные (рис. 6.2) спроектируем цифровой фильтр с бесконечной импульсной характеристикой (IIR-фильтр). На рис. 6.5 представлен полосовой фильтр Баттерворта. В области Current Filter Information указано, что этот фильтр реализован передаточной функцией 60 порядка, которая в программе fdatool представлена формой, состоящей из 30 секций второго порядка. Вход в подменю Convert Structure из меню Edit дает представление о структурах, которые могут быть использованы при реализации IIR-фильтров. Эта информация справочная, так как при проектировании IIR-фильтры реализуются единственным способом – в виде прямой формы, состоящей из секций второго порядка (Direct form II, second-order sections). Принципиальную схему этого фильтра можно сохранить в mdl-файле, вызвав команду Realize Model.
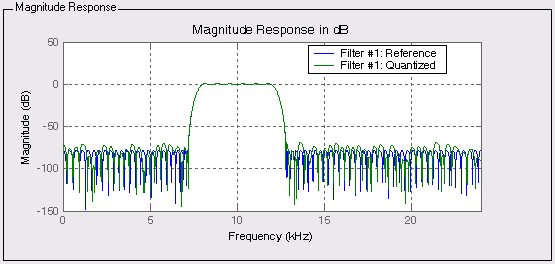
Рис. 6.4. АЧХ фильтра-прототипа и квантованного фильтра
с конечной импульсной характеристикой
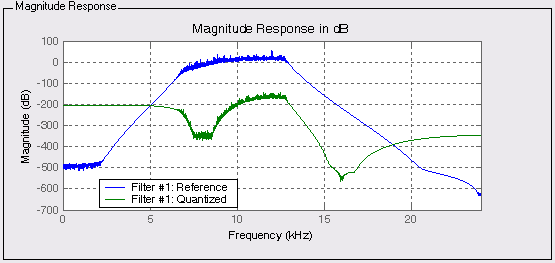
Рис. 6.5. АЧХ исходного (Referenсe) и квантованного (Quantized) фильтров
После нажатия кнопки Set Quantization Parameter перейдем к окну расчета цифрового фильтра с учетом квантования. Для запуска процесса расчета необходимо установить флажок Turn Quantization. Данные расчета приведены на рис. 6.5. Коэффициенты фильтра будут задаваться с ограниченной точностью, параметры квантования заданы по умолчанию.
Из сравнения кривых на рис. 6.5 видно, что учет квантования значительно изменил АЧХ нового цифрового фильтра.
Свойства квантованных фильтров зависят от многих факторов: формата данных, реализации операций, выбора арифметики и структуры представления фильтра. В рассматриваемом пакете фильтр с бесконечной импульсной характеристикой (IIR-фильтр) реализуется блочной структурой как менее чувствительной к изменению значений коэффициентов.
Учет квантования по уровню делает систему нелинейной. Масштабирование коэффициентов, исключение переполнения разрядной сетки и другие приемы, связанные с нормализацией коэффициентов фильтра, значительно уменьшают ошибки квантования. В FDAtool установлена подпрограмма Optimization, команды которой приведены на рис. 6.6.
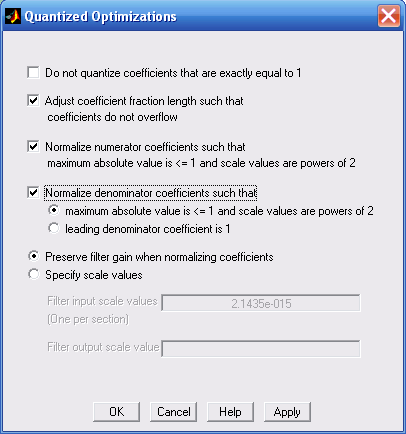
Рис. 6.6. Команды подпрограммы Optimization
При нажатии кнопки Optimization приблизим характеристики квантованного фильтра к фильтру-прототипу (рис. 6.7).
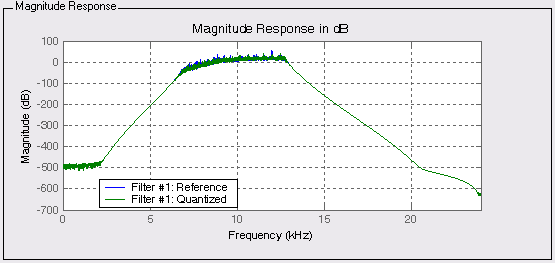
Рис. 6.7. АЧХ фильтра-прототипа и дискретного фильтра с учетом квантования
после использования подпрограммы Optimization
Задание
1. Для заданного варианта заполнить поля, определяющие параметры АЧХ проектируемого фильтра.
2. Для фильтра с конечной импульсной характеристикой найти:
– амплитудно-фазовую характеристику;
– фазочастотную характеристику;
– импульсную переходную характеристику;
– переходную характеристику;
– расположение нулей и полюсов;
– структурную схему фильтра и его коэффициенты с помощью Realize Model.
3. Перенести структурную схему в отчет.
4. Для фильтра с бесконечной импульсной характеристикой найти:
– амплитудно-фазовую характеристику;
– фазочастотную характеристику;
– импульсную переходную характеристику;
– переходную характеристику;
– расположение нулей и полюсов;
– структурную схему фильтра и его коэффициенты с помощью Realize Model.
5. Перенести структурную схему в отчет.
6. При помощи Set Quatization Parametrs определить характеристику FIR фильтра с учетом квантования, для чего установить флажок Turn quantization on, делающий активными поля, в которых задаются требования к форме представления коэффициентов. В окне AЧX фильтров появятся два графика: у первого коэффициенты передаточной функции заданы с машинной точностью, у второго – в коэффициентах учтено квантование по уровню.
7. Выполнить операцию «Оптимизация», подставив флажки, нормирующие коэффициенты фильтра.
8. Вычислить AЧX фильтра с учетом квантования после выполнения операции «Оптимизация».
9. Сравнить характеристики цифровых FIR-фильтров для вариантов:
‑ коэффициенты фильтра определены с машинной точностью;
‑ коэффициенты фильтра определены с учетом квантования без «Оптимизации»;
‑ коэффициенты фильтра определены с учетом квантования и применения процедуры «Оптимизация».
10. Выполнить пункты 6 – 9 применительно к IIR-фильтрам.
11. Сравнить характеристики FIR- и IIR-фильтров и сделать выводы.
Содержание отчета
1. Краткие теоретические сведения о фильтрах с конечной (FIR) и бесконечной (IIR) импульсными характеристиками, о квантовании сигналов по уровню, о процедурах уменьшения погрешностей при квантовании сигналов.
2. Результаты испытания FIR-фильтров для трех форм задания коэффициентов.
3. Результаты испытания IIR-фильтров для трех форм задания коэффициентов.
4. Сравнительные характеристики FIR- и IIR-фильтров.
5. Выводы.
Контрольные вопросы
1. Основное отличие между фильтрами с бесконечными и конечными импульсными характеристиками (IIR или FIR).
2. Какие параметры отличают режекторный и полосовой фильтры?
3. По каким параметрам отличаются фильтр низких частот и фильтр высоких частот?
4. Как влияет порядок фильтра на его амплитудно-частотную характеристику?
5. Как влияет порядок фильтра на его фазочастотную характеристику?
6. Что влияет на количество граничных частот при проектировании фильтра?
7. Какие приемы используются для оптимизации цифрового фильтра?
8. Какая частота называется частотой Найквиста?