1 ‑ Дискретный (c2d); 2 ‑ дискретный (impinvar); 3 ‑ аналоговый
Передаточные функции, полученные путем расчетов (5.16) – (5.19) и с помощью процедуры impinvar, совпадают. Логарифмические характеристи-ки, полученные с применением разных процедур, отличаются: меньшую ошибку дает процедура impinvar.
Определим передаточную функцию дискретного фильтра с помощью подстановки оператора s (5.8) в исходную формулу аналогового фильтра:
,
(5.20)
Процедуру определения параметров цифрового фильтра на основе метода билинейного преобразования можно ускорить, воспользовавшись процедурами bilinear или c2d.
К процедуре bilinear можно обратиться тремя способами:
[bd,ad]=bilinear(b,a,Fs,Fp); (5.21)
[zd,pd,kd]=bilinear(z,p,kFs,Fp); (5.22)
[Ad,Bd,Cd,Dd]=bilinear(А,В,С,D,Fs,Fp). (5.23)
Исходными данными для выполнения процедуры bilinear являются параметры: Fs, задающий частоту дискретизации, и Fp, определяющий частоту, на которой значения АЧХ до и после выполнения преобразования должны совпадать.
Выражения (5.21) – (5.23) отличаются формой представления исходных данных. В (5.21) определяют коэффициенты числителя bd и знаменателя ad дискретного фильтра по коэффициентам числителя b и знаменателя a аналогового прототипа. В выражении (5.22) исходными данными аналогового прототипа являются нули z, полюса р и коэффициент усиления k. Обращение к выражению (5.22) позволяет вычислить нули zd, полюса pd и коэффициент усиления kd дискретного фильтра. И, наконец, выражение (5.23) определяет дискретную матрицу пространства состояния фильтра по известным непрерывным матрицам пространства состояния этого фильтра.
Процедура c2d определяет параметры дискретного фильтра по непрерывной передаточной функции h и интервалу дискретности ТП:
hd=c2d(h,Tp,'метод'). (5.24)
Matlab предлагает несколько методов аппроксимации: нулевого порядка, первого порядка, билинейной аппроксимации Тастина, билинейной аппроксимации Тастина с коррекцией и соответствия нулей и полюсов. При выборе метода аппроксимации выражение (5.24) конкретизируется, например, при применении билинейной аппроксимации Тастина:
hd=c2d(h,Tp,'TUSTIN'). (5.25)
Расчет цифровых фильтров с помощью билинейного преобразования проиллюстрирован программой
h=tf([2],[1,7,10]) %Исходные данные
syms z s %Ввод символьных переменных
k=2;Tp=0.1; %Числовые значения переменных
s=(2/Tp)*(1-z^-1)/(1+z^-1) %Переход на плоскость W
hs=2/(s^2+7*s+10) %Применение преобразования к аналоговому фильтру
hs1=simplify(hs) %Алгебраические преобразования
hs2=filt([1,2,1],[1,-1.4182,0.4909],Tp)*(1/275) %Уравнение
%цифрового фильтра при билинейном преобразовании
[n,d,t]=tfdata(h,'v') %Определение коэффициентов
%передаточной функции непрерывного фильтра
[nd,dd]=bilinear(n,d,1/Tp) %Уравнение цифрового фильтра при
%билинейном преобразовании
Tp=0.1;
hdt=c2d(h,Tp,'TUSTIN') %Уравнение цифрового фильтра при
%преобразовании Тастина
hdv=filt(nd,dd,Tp) %Приведение уравнения к форме фильтра
bode(h,hdt,hdv,hs2),grid on %Логарифмические характеристики
%аналоговых и цифровых фильтров.
Результаты расчетов этой программы приведены на рис. 5.4, из которого следует, что графики частотных характеристик, полученные путем трудоемких расчетов (5.20) и с помощью процедур bilinear и c2d, совпадают. Учитывая то, что процедуры bilinear и c2d равнозначны, но в процедуре c2d исходные данные задаются в более компактном виде, расчеты цифровых фильтров целесообразно выполнять методом билинейной аппроксимации.
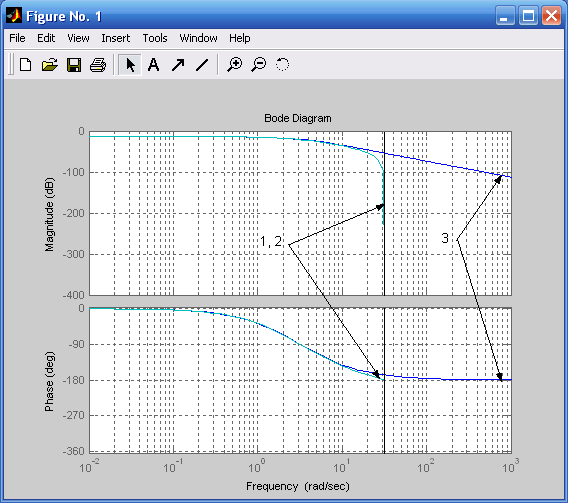
Рис. 5.4. Логарифмические характеристики фильтров: