Лабораторная работа № 5 Проектирование дискретных фильтров по аналоговому эквиваленту

Цель работы

1. Изучение и проверка эффективности методик расчета дискретных фильтров по аналоговым эквивалентам, частотные характеристики которых определяют требования к дискретным фильтрам.

2. Получение навыков в расчете дискретных фильтров на основе аппроксимации Эйлера.

3. Получение навыков в расчете дискретных фильтров на основе инвариантного преобразования импульсной переходной функции.

4. Получение навыков в расчете дискретных фильтров на основе билинейного преобразователя.

Теоретическое обоснование

Существует несколько подходов к проектированию цифровых фильтров. Один из распространенных подходов состоит в следующем.

1. Определяют передаточную функцию аналогового фильтра H(s), которая удовлетворяет требованиям частотной обработки сигналов, то есть в которой заданы интервалы частот пропускания и задерживания, допустимые величины амплитудных искажений сигналов в полосах пропускания и задерживания.

2. По заданной передаточной функции H(s) определяют дискретную передаточную функцию фильтра H(z), которая удовлетворяет требованиям, предъявляемым к фильтру H(s).

Переход от H(s) к H(z) можно осуществить тремя путями:

– аппроксимацией Эйлера;

– инвариантным преобразованием импульсной переходной функции;

– с помощью билинейного преобразования.

Аппроксимация Эйлера

При аппроксимации Эйлера исходные данные аналогового фильтра могут быть заданы в двух модификациях: через дифференциальные уравнения или через передаточные функции. Переход от дифференциального уравнения к разностному осуществляется путем замены производных соответствующими разностями:

, (5.1)

.

Переход от H(s) к H(z) можно осуществить, заменив непрерывный оператор s на его дискретный аналог:

. (5.2)

Как следует из выражения (5.1) и (5.2) ошибка перехода от непрерыв-ного представления к дискретному зависит от интервала дискретности Т_П. Поэтому частотные характеристики дискретного фильтра в полосе пропускания будет приближаться к частотным характеристикам аналогового фильтра только при условии, что интервал дискретизации Т_П достаточно мал.

Инвариантное преобразование импульсной переходной функции

Построение цифровых фильтров по их аналоговому прототипу заключается в преобразовании параметров аналогового фильтра в параметры дискретного фильтра, при котором импульсные характеристики фильтров (аналогового и дискретного) совпадают в дискретные моменты времени при t = nТ_П.

Математически условие совпадения импульсных характеристик фильтров (аналоговых и дискретных) записывается как

, (5.3)

где h(t), hd(t) – импульсные характеристики аналоговых и дискретных фильтров соответственно.

Передаточная функция аналогового фильтра

, (5.4)

где, s_i –полюса (корни) передаточной функции аналогового фильтра; A_i – коэффициенты, определенные любым из известных методов; m – степень характеристического уравнения знаменателя.

Аналогично (5.4) может быть получена z-передаточная функция дискретного фильтра, представленная в виде суммы дробей:

. (5.5)

При сравнении (5.4) и (5.5) получают выражение для перехода от анало-говых фильтров к цифровым фильтрам по методу инвариантного преобразования импульсной переходной характеристики

. (5.6)

.

Метод преобразования импульсной переходной функции базируется на связи точек плоскости S с точками плоскости Z, определяемой отношением

, (5.7)

где θ – угол между действительной осью плоскости Z и векторами, определяющими точки на окружности единичного радиуса плоскости Z.

Билинейное преобразование

Из (5.7) следует, что связь между точками плоскости S и Z неоднозначна, то есть цифровой фильтр не будет адекватен его аналоговому прототипу. Например, частоты ω = 0; ω = 2π/Т_П и ω = 4π/Т_П на плоскости Z отображаются в одну точку z = 1.

Для исключения нежелательного эффекта вводят билинейное преобразование, которое однозначно преобразует точки мнимой оси плоскости S в точки мнимой оси плоскости Z с помощью выражений (5.7) и (5.8). Выражение (5.7) преобразует мнимую ось плоскости S в окружность единичного радиуса плоскости Z, а выражение (5.8) преобразует мнимую ось плоскости S в мнимую ось плоскости Z. Выражение (5.8) известно как W-преобразование и плоскость Z при таком преобразовании обозначается как плоскость W:

. (5.8)

Решая уравнение (5.8) относительно z получают выражение, определяющее переход из плоскости W в плоскость S:

. (5.9)

Методика расчета цифровых фильтров базируется на выражениях (5.8), (5.9) и состоит из следующих шагов:

1) определение передаточной функции аналогового фильтра H(s);

2) применение к H(s) билинейного преобразования и получение z-пере-даточной функции цифрового фильтра:

. (5.10)

При преобразовании (5.10) у цифрового фильтра будут сохраняться форма частотных характеристик и свойства устойчивости аналогового фильтра. Связь между ω и θ будет нелинейной:

, (5.11)

θ = ωТ_П. (5.12)

Из выражений (5.11) и (5.12) можно сделать вывод, что по заданной круговой частоте ω можно определить цифровую частоту θ, а по заданной цифровой частоте θ можно определить круговую частоту ω. Изменением интервала дискретности можно менять коэффициент пропорциональности между θ и ω (5.11), что позволяет изменять АЧХ цифровых фильтров.

Описание работы

Пусть задана передаточная функция фильтра низких частот

.

Необходимо найти соответствующий цифровой фильтр. Учитывая соотношение (5.2), получим дискретную передаточную функцию фильтра H(z):

(5.13)

При Т_П = 0,1 и Т_П = 0,01 выражение (5.13) будет представлено в следующем виде:

, (5.14)

. (5.15)

Переход от непрерывного описания процессов к их дискретному представлению можно упростить, воспользовавшись пакетом Matlab.

h=tf([2],[1,7,10]) %Передаточная функция непрерывного фильтра

Tp=0.1; %Интервал дискретности

hd=c2d(h,Tp) %Передаточная функция дискретного фильтра

syms z s %Ввод символьных переменных

k=2; %Ввод коэффициента усиления

s=(1-z^-1)/Tp %Переход от непрерывного оператора к дискретному

hs=k/(s^2+7*s+10) %Исходное уравнение

hs1=simplify(hs) %Компактное представление исходных данных

dd=filt([0.2,0,0],[18,-27,10],Tp) %Дискретная передаточная функция

%(аппроксимация Эйлера)

figure(1)

bode(h,dd,hd),grid on %Логарифмические характеристики

Tp=0.01; %Интервал дискретности 0,01

hd=c2d(h,Tp) %Передаточная функция дискретного фильтра

syms z s %Ввод символьных переменных

k=2; %Ввод коэффициента усиления

s=(1-z^-1)/Tp %Ввод символьных переменных

hs=k/(s^2+7*s+10) %Исходное уравнение

hs2=simplify(hs) %Компактное представление исходных данных

dd2=filt([0.2,0,0],[1071,-2070,1000],Tp)

%Передаточная функция фильтра

figure(2) %Логарифмические характеристики

bode(h,hd,dd2),grid on %1-непрерывный фильтр

%2-дискретный (команда c2d), 3-аппроксимация Эйлера.

На рис. 5.1 и 5.2 представлены фильтры при разных методах аппроксимации: 1 ‑ дискретный (команда c2d); 2 ‑ дискретный (аппроксимация Эйлера); 3 ‑ аналоговый. Из рис. 5.1 и 5.2 следует, что при изменении периода дискретизации Т_П наблюдается различие частотных характеристик в области рабочих частот, на которых ослабление сигнала не превышает –40 дБ. При Т_П = 0,1 с дискретный фильтр, сформированный командой c2d, более устойчив в области рабочих частот, при Т_П = 0,01 с дискретный фильтр, сформированный командой c2d, менее устойчив, чем дискретный фильтр, полученный с помощью аппроксимации Эйлера.

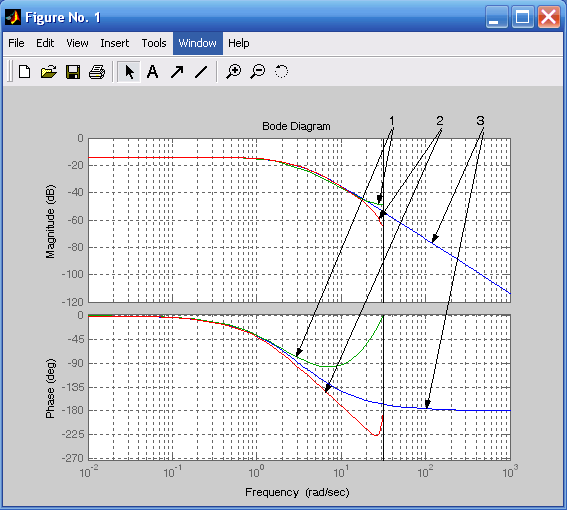
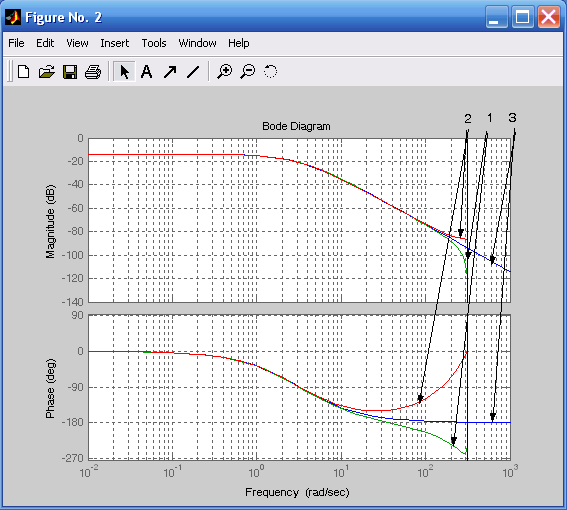
Рис. 5.1. Логарифмические характеристики Рис. 5.2. Логарифмические характеристики

фильтров при Т_П = 0,1с фильтров при Т_П = 0,01 с

Рассмотрим применение второго способа. Пусть задана передаточная функция аналогового фильтра

.

Необходимо построить цифровой фильтр методом инвариантного преобразования импульсной переходной функции.

Представим передаточную функцию H(s) в виде простых дробей

. (5.16)

Определим A₁ и A₂ методом Хевисайда:

, .

Используя соотношения (5.6) и (5.16) запишем z-передаточную функцию цифрового фильтра как

. (5.17)

Упрощая выражение (5.17), получим

. (5.18)

При Т_П = 0,1 с, получим

. (5.19)

Трудоемкие вычисления, связанные с переходом от непрерывных передаточных функций к дискретным, можно исключить с помощью процедуры:

[bd,ad]=impinvar(b,a,Fs),

где b, a – заданные векторы коэффициентов числителя и знаменателя передаточной функции аналогового прототипа; Fs – частота дискретизации сигнала; bd, ad – вычисленные коэффициенты числителя и знаменателя дискретной передаточной функции дискретного фильтра.

Процедура определения параметров дискретного фильтра по его аналоговому прототипу базируется на совпадении импульсных характеристик обоих фильтров в точках квантования сигналов:

h=tf([2],[1,7,10]) %Передаточная функция непрерывного фильтра

Tp=0.1; %Интервал дискретности

hd=c2d(h,Tp) %Передаточная функция дискретного фильтра

[n,d,t]=tfdata(h,'v') %Определение коэффициентов передаточной

%функции непрерывного фильтра

[nd,dd]=impinvar(n,d,1/Tp) %Определение коэффициентов передаточной

%функции дискретного фильтра

f=Tp*filt([0,0.0141,0],[1,-1.4253,0.4966],Tp)*10 %Передаточная

%функция нормированного дискретного фильтра

bode(h,hd,f),grid on %Логарифмические характеристики

%проектируемых фильтров.

Результаты моделирования изображены на рис. 5.3. Усиление цифрового фильтра на нулевой частоте равно 1/Т_П, а усиление аналогового фильтра при ω = 0 составляет 1. Если сравнить выражение (5.19) с аналогичным выражением, полученным ранее, то наблюдается расхождение, определяемое множителем Т_П. Чтобы привести в соответствие результаты расчетов, полученные аналитическим путем (5.16) – (5.19), с результатами расчетов, полученными ранее в пакете Matlab, следует пронормировать выражение (5.19), умножив его на величину, обратную частоте дискретизации.

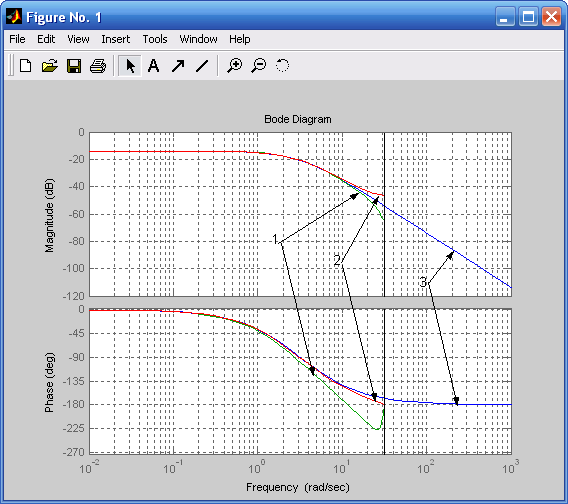
Рис. 5.3. Логарифмические характеристики фильтров: