Лабораторная работа № 4 Исследование характеристик аналоговых и дискретных фильтров

Цель работы

1. Изучение частотных характеристик аналоговых и дискретных фильтров.

2. Аналитические исследования аналоговых и дискретных фильтров в пакетах Control System Toolbox.

3. «Экспериментальные» исследования аналоговых и дискретных фильтров в пакете Simulink.

Теоретическое обоснование

Фильтр – это устройство или программа, которая обеспечивает частотно-зависимые преобразования входного сигнала. Для фильтра низких частот устройства или программы должны обеспечивать отсутствие амплитудных искажений входного сигнала в области частот от 0 до некоторой заданной _С и эффективное подавление частот, которые превышают граничную частоту _С.

Аналоговый фильтр может быть представлен непрерывной передаточной функцией

,

где, Y(s), X(s) – изображение по Лапласу выходного и входного сигналов фильтра, соответственно; M(s), N(s) – полиномы числителя и знаменателя передаточной функции.

В качестве основных характеристик фильтра принимают характеристику затухания A(), которая является величиной, обратной модулю частотной передаточной функции:

A(ω) = 20 lg{W(jω)^–1} = 10 lg L(ω²),

фазовую характеристику Q():

Q() = arg(W(jω))

и характеристику групповой задержки :

.

Функцию

L(ω²) = |W(s)·W(–s)^–1|

называют функцией затухания.

Идеальный фильтр низких частот (ФНЧ) пропускает только низкочастотные составляющие. Его амплитудно-частотная характеристика имеет вид, приведенный на рис. 4.1.

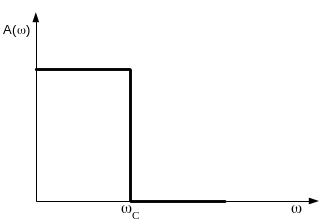
Рис. 4.1. Амплитудно-частотная характеристика идеального ФНЧ

Диапазон частот от 0 до _С называется полосой пропускания, остальной частотный диапазон – полосой задерживания. Граница между этими полосами _С называется частотой среза. В реальных фильтрах переход от частоты пропускания к частоте задерживания происходит плавно (рис. 4.2).

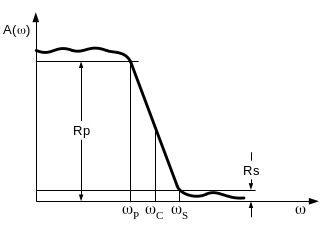
Рис. 4.2. Амплитудно-частотная характеристика реального ФНЧ

На рис. 4.2 показаны контрольные точки ФНЧ, которые используются при его проектировании:

_P – граничная частота пропускания;

_S – граничная частота задерживания;

_С – частота среза;

R_P – максимально допустимое подавление сигнала в полосе пропускания, дБ;

R_S – минимально допустимое подавление сигнала в полосе задерживания, дБ.

Команда buttord определяет порядок n характеристического уравнения передаточной функции и частоту среза _С аналогового фильтра Баттерворта с учетом заданных частот пропускания и задерживания (_P, _S), максимально допустимых подавлений сигналов в полосе пропускания и задерживания (R_P, R_S).

Если команда buttord содержит параметр s

[n,WC]=buttord(Wp,Ws,Rp,Rs,’s’),

то частоты _P, _S должны быть заданы в радианах в секунду, значения частоты _С также будет получено в радианах за секунду.

Если команда buttord не содержит параметр s

[n,WC]=buttord(wp,ws,RP,RS),

то частоты _P и _S задают в относительных единицах /_B, изменяющихся от 0 до 1, где 1 соответствует частоте _B, определяемой выражением:

,

где Т_П - период дискретности.

При построении дискретного фильтра, соответствующего данному аналоговому фильтру, _B является частотой, на которой наблюдается максимальное различие между амплитудными значениями аналогового и дискретного фильтров и по этому расхождению можно оценить правильность выбора Т_П. В то же время _B – это частота, выше которой частотными характеристиками аналогового сигнала можно пренебречь.

В пакете Control System Toolbox аналоговые и цифровые фильтры могут быть представлены:

– в виде уравнений пространства состояний – форма ss;

– через передаточные функции – форма tf;

– через нули и полюса – форма zpk.

Переход от непрерывного представления уравнений к их дискретному представлению определяется командой c2d, а переход к непрерывному представлению, если задан его дискретный аналог, определяется командой d2c.

Описание работы

Приведенные теоретические положения рассмотрены ниже:

Wp=1; %Граничная частота пропускания

Ws=10; %Граничная частота задержки

Rp=6; %Максимально допустимое подавление в полосе пропускания

Rs=20; %Минимально допустимое подавление в полосе задерживания)

[n,Wn]=buttord(Wp,Ws,Rp,Rs,'s') %Определение параметров

%аналогового фильтра Баттерворта

[z,p,k]=buttap(n); %Определение нулей и полюсов фильтра Баттерворта

[b,a]=zp2tf(z,p,k) %Определение коэффициентов фильтра Баттерворта

h=tf([b],[a]) %Определение передаточной функции

%аналогового фильтра Баттерворта

%Проектирование фильтра Баттерворта с более жесткими требованиями

Wp=1;

Ws=10;

Rp=2; %Снижено максимально допустимое подавление

Rs=20;

[n2,Wn2]=buttord(Wp,Ws,Rp,Rs,'s')

[z,p,k]=buttap(n2);

[b2,a2]=zp2tf(z,p,k)

h2=tf([b2],[a2]) %Определение передаточной функции

%аналогового фильтра Баттерворта.

%Проектирование фильтра Баттерворта с более жесткими требованиями

Wp=1;Ws=10;

Rp=2;Rs=52; %Увеличено максимально допустимое подавление

[n3,Wn2]=buttord(Wp,Ws,Rp,Rs,'s')

[z,p,k]=buttap(n3);

[b3,a3]=zp2tf(z,p,k)

h3=tf([b3],[a3]) %Определение передаточной функции

%аналогового фильтра Баттерворта.

figure(1) %Построение ЛЧХ для трех фильтров Баттерворта

bode(h,h2,h3),grid on %Рис. 4.3

%Проектирование дискретных фильтров Баттерворта при t=0,2

t=0.2; %Интервал дискретности

hd=c2d(h,t) %Передаточная функция дискретного Фильтра,

%соответствующая аналоговому фильтру h

h2d=c2d(h2,t) %Передаточная функция дискретного Фильтра,

%соответствующая аналоговому фильтру h2

h3d=c2d(h3,t) %Передаточная функция дискретного Фильтра,

%соответствующая аналоговому фильтру h3

figure(2) %ЛАЧ и ЛФЧ характеристики фильтров h и hd

bode(h,hd),grid on %Рис. 4.4

figure(3) %ЛАЧ и ЛФЧ характеристики фильтров h2 и h2d

bode(h2,h2d),grid on %Рис. 4.5

figure(4) %ЛАЧ и ЛФЧ характеристики фильтров h3 и h3d

bode(h3,h3d),grid on %Рис. 4.6

%Проектирование дискретных фильтров Баттерворта при t=0,05

t=0.05; %Интервал дискретности

hd=c2d(h,t) %Определение параметров дискретных фильтров

h2d=c2d(h2,t) %для спроектированных непрерывных фильтров

h3d=c2d(h3,t) %при новых интервалах дискретности.

figure(5) %Построение ЛАЧ и ЛФЧ характеристик (рис. 4.7)

bode(h,hd),grid on %аналоговых и дискретных (при измененном

figure(6) %интервале дискретности)фильтров

bode(h2,h2d),grid on %Рис. 4.8

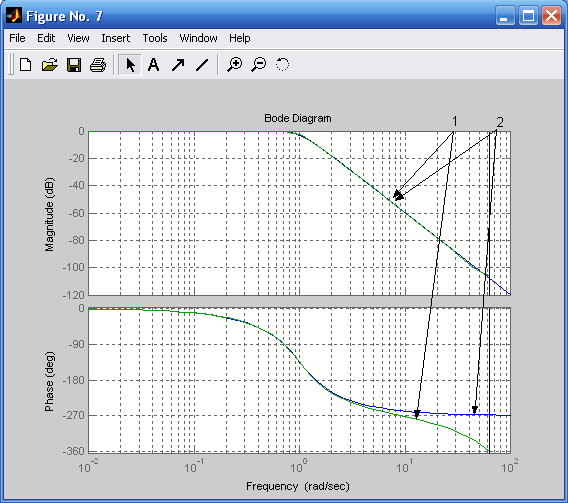
figure(7) %Рис. 4.9

bode(h3,h3d),grid on.

Частотные характеристики реализованных в программе фильтров представлены на рис. 4.3 – 4.9, при этом на рис. 4.7 – 4.9 представлены характеристики фильтров, имеющих одинаковые частоты ω_P и ω_S, но разные величины допустимого подавления сигнала R_P и R_S.

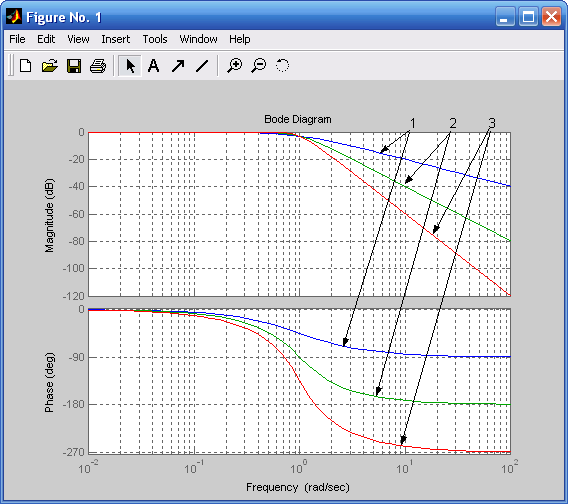
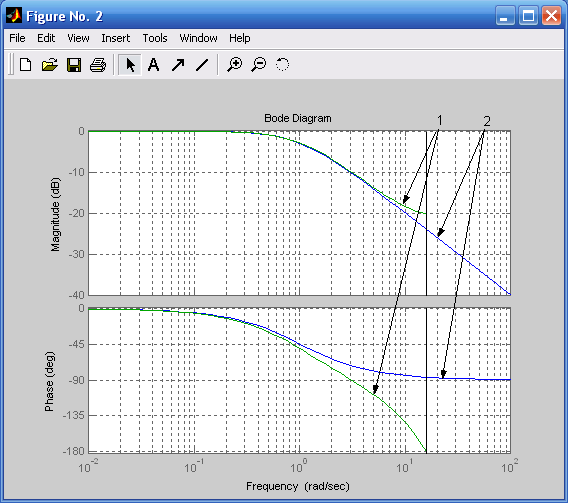
Рис. 4.3. ЛЧХ аналоговых фильтров Баттерворта: Рис. 4.4. ЛЧХ дискретного (1) и

1 – фильтр первого порядка (–20 дБ/дек.); аналогового (2) фильтров

2 – фильтр второго порядка (–40 дБ/дек.); Баттерворта (ФНЧ первого

3 – фильтр третьего порядка (–60 дБ/дек.) порядка)

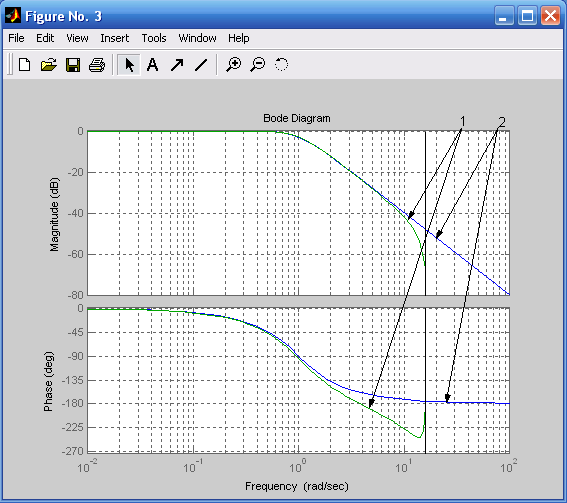
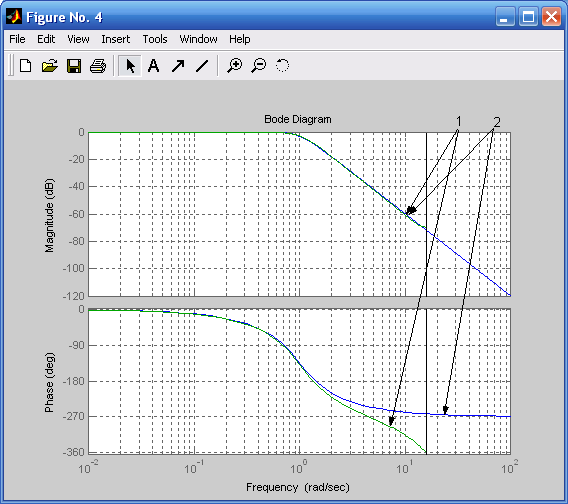
Рис. 4.5. ЛЧХ дискретного (1) и аналогового Рис. 4.6. ЛЧХ дискретного (1) и аналогового

(2) фильтров Баттерворта (ФНЧ второго (2) фильтров Баттерворта (ФНЧ третьего

порядка) при Rp = 2 дБ порядка) при Rs = 52 дБ

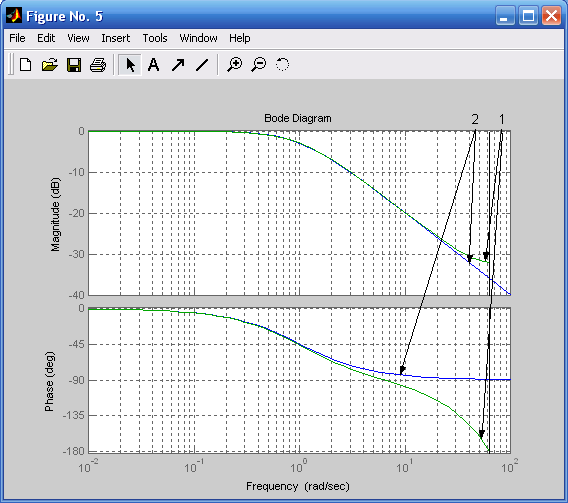
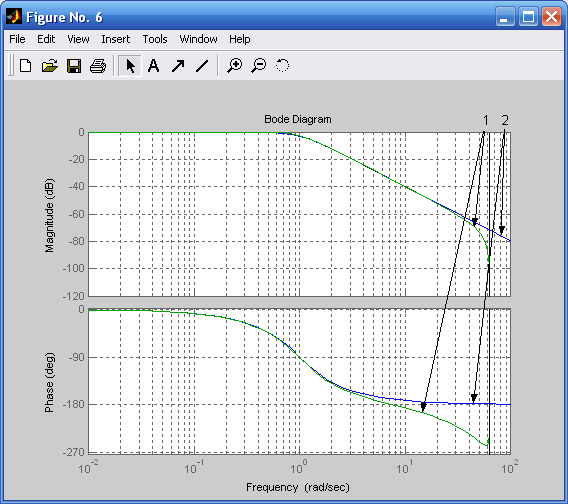
Рис. 4.7. ЛЧХ дискретного (1) и аналогового Рис. 4.8. ЛЧХ дискретного (1) и аналогового

(2) фильтров Баттерворта при Т_П = 0,05 с (2) фильтров Баттерворта при Т_П = 0,05 с

(ФНЧ первого порядка) и Rp = 2 дБ (ФНЧ второго порядка)

Порядок фильтра будет увеличиваться при уменьшении R_P, увеличении R_S, при сближении ω_P и ω_S и повышении фильтрующих свойств (рис. 4.3). Связь между параметрами ω_P, ω_S, R_P, R_S (требованиями к фильтру) и порядком фильтра иллюстрируется примерами рис. 4.3 – 4.9.

Командой c2d определяют z-передаточные функции фильтров первого, второго и третьего порядков Для Т_П = 0,2 с имеем передаточные функции:

, (4.1)

, (4.2)

. (4.3)

Z–передаточные функции для Т_П = 0,05 с представлены ниже:

, (4.4)

, (4.5)

. (4.6)

-

Рис. 4.9. ЛЧХ дискретного (1) и аналогового (2)

фильтров Баттерворта при Т_П = 0,05 с

и Rs = 52 дБ (ФНЧ третьего порядка)

Между амплитудными и фазовыми характеристиками непрерывного и дискретного фильтров на частоте ω_С наблюдаются значительные различия. Уменьшение Т_П (рис. 4.7 – 4.9) позволяет приблизить характеристики дискретного фильтра к аналоговому в области высоких частот.

По полиномам числителя и знаменателя передаточной функции ФНЧ команда lp2lp определяет передаточные функции с новыми частотами среза:

[b1,a1]=lp2lp(b,a,W0),

где b, а – коэффициенты исходного фильтра низких частот; W0 – желаемая

частота среза проектируемого фильтра; b1, a1 – коэффициенты спроектированного фильтра с новыми частотами среза.

Ниже приведены примеры определения передаточных функций ФНЧ для трех частот среза. Командой buttap определяют нули, полюса и коэффициент усиления фильтра. Команда zp2tf преобразует математическую модель ФНЧ – от модели, заданной нулями, полосами и коэффициентом усиления, к модели, представленной передаточными функциями.

wr=0.1; %Частота пропускания в относительных единицах

ws=0.6; %Частота задерживания в относительных единицах

rp=6; %Допустимое подавление в полосе пропускания

rs=40; %Допустимое подавление в полосе задерживания

[n1,wc1]=buttord(wr,ws,rp,rs) %Определение параметров фильтра

[z1,p1,k1]=buttap(n1); %Определение фильтра Баттерворта в форме zpk

[b1,a1]=zp2tf(z1,p1,k1) %Полиномы числителя и знаменателя фильтра

h1=tf([b1],[a1]) %Определение фильтра Баттерворта в форме tf

w1=10; %Частота среза проектируемого фильтра Баттерворта

[b10,a10]=lp2lp(b1,a1,w1) %Параметры фильтра на частоте w1

w2=100; %Частота среза проектируемого фильтра Баттерворта

[b100,a100]=lp2lp(b1,a1,w2) %Параметры фильтра частотой среза w2

q1=tf([b10],[a10]) %Передаточная функция с частотой среза w1

q2=tf([b100],[a100]) %Передаточная функция фильтра Баттерворта

%с частотой среза w2.

figure(1) %Логарифмические характеристики проектируемых фильтров

bode(h1,'g',q1,'k',q2,'r'),grid on %при разных частотах среза.

Результаты выполнения программы приведены на рис. 4.10. По передаточным функциям, определённым в программе, на рис. 4.11 представлены структурные схемы непрерывных и дискретных фильтров низких частот.

Рис. 4.10. Логарифмические характеристики непрерывного ФНЧ второго порядка для

разных частот среза: 1 – частота среза 1 с^-1; 2 – частота среза 10 с^-1; 3 – частота среза 100 с^-1

^{А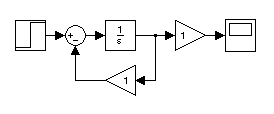 В}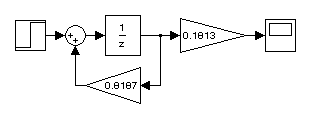

^С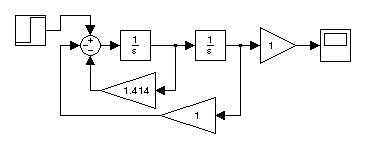

^D

^E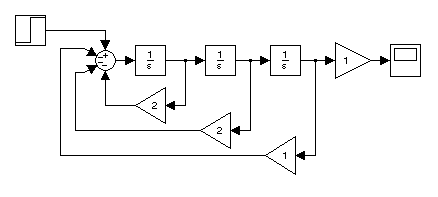

^F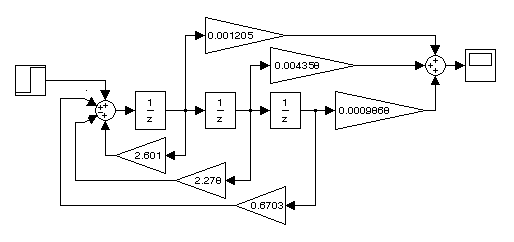

Рис. 4.11. Структурные схемы непрерывных и дискретных ФНЧ: А, C, E – непрерывная

передаточная функция в форме tf фильтров I, II, III порядков соответственно;

B, D, F – реализация их z-передаточной функции на регистрах сдвига

Задание

1. По заданным параметрам проектируемого ФНЧ (ω_R – граничная частота пропускания, ω_S – граничная частота задерживания, R_P – значение максимально допустимого подавления сигнала в полосе пропускания, R_S – значение максимально допустимого подавления сигнала в полосе задерживания) определить его передаточную функцию.

2. Определить передаточную функцию ФНЧ, изменяя исходные данные так, чтобы частоты пропускания и задерживания оставались неизменными, а максимально допустимое подавление в полосе пропускания уменьшалось в 3 раза.

3. Определить передаточную функцию ФНЧ, изменяя исходные данные так, чтобы частоты пропускания и задерживания оставались неизменными, а максимально допустимое подавление в полосе задерживания увеличивалось в 3 раза.

4. Выполнить программу и построить логарифмические характеристики аналоговых фильтров.

5. Для заданного интервала дискретности Т_П определить граничную частоту.

6. По заданным параметрам (табл.1) составить программу расчета дискретных фильтров Баттерворта.

7. Выполнить программу и построить логарифмические характеристики дискретных фильтров.

8. По передаточным функциям аналоговых и дискретных фильтров в пакете Simulink составить структурные схемы.

9. Пересчитать частоты пропускания и задерживания известного ФНЧ в относительные единицы и определить передаточную функцию фильтра Баттерворта.

10. Определить параметры фильтра Баттерворта при увеличенных в 10 и 100 раз частотах среза.

11. Для одного из спроектированных аналоговых фильтров Баттерворта определить передаточную функцию дискретного фильтра.

12. Уменьшить интервал дискретности в 4 раза и при новых параметрах определить передаточную функцию дискретного фильтра.

13. В пакете Simulink промоделировать структурные схемы аналоговых и дискретных фильтров.

Содержание отчета

1. Краткая характеристика фильтра.

2. Методика расчёта непрерывных фильтров Баттерворта по заданным техническим требованиям.

3. Методика расчёта дискретных фильтров Баттерворта по заданным техническим требованиям.

4. Структурные схемы, реализующие дискретные фильтры по передаточным функциям и на блоках задержки.

5. Анализ результатов расчета и моделирования аналоговых и дискретных фильтров.

Контрольные вопросы

1. Какой вид имеют логарифмические характеристики фильтров низких частот?

2. Какой вид имеют логарифмические характеристики фильтров высоких частот?

3. Укажите на графиках точку, определяющую граничную частоту пропускания, и обоснуйте методику ее определения.

4. Укажите на графиках точку, определяющую граничную частоту задерживания, и обоснуйте методику ее определения.

5. Во сколько раз амплитуда выходного сигнала будет меньше амплитуды входного сигнала, если величина подавления составляет 6 дБ?

6. Во сколько раз амплитуда выходного сигнала будет меньше амплитуды входного сигнала, если величина подавления составляет 2 дБ?

7. Как и почему будет изменяться степень характеристического уравнения фильтра Баттерворта, если интервал между граничной частотой пропускания и задерживания будет уменьшаться?

8. Как и почему будет изменяться степень характеристического уравнения фильтра Баттерворта, если интервал между граничной частотой пропускания и задерживания будет увеличиваться?

9. Как и почему будет изменяться степень характеристического уравнения фильтра Баттерворта, если максимально допустимое подавление в полосе частот пропускания будет уменьшаться?

10. Как и почему будет изменяться степень характеристического уравнения фильтра Баттерворта, если максимально допустимое подавление в полосе частот пропускания будет увеличиваться?

11. Как и почему будет изменяться степень характеристического уравнения фильтра Баттерворта, если максимально допустимое подавление в полосе частот подавления будет уменьшаться?

12. Как и почему будет изменяться степень характеристического уравнения фильтра Баттерворта, если максимально допустимое подавление в полосе частот подавления будет увеличиваться?

13. Какие исходные данные следует знать, чтобы получить передаточную функцию фильтра Баттерворта с заданной частотой среза?

14. Как определить характеристику затухания для фильтра Баттерворта и какой график она имеет?