Impz(b,a),grid on %Импульсная характеристика фильтра.

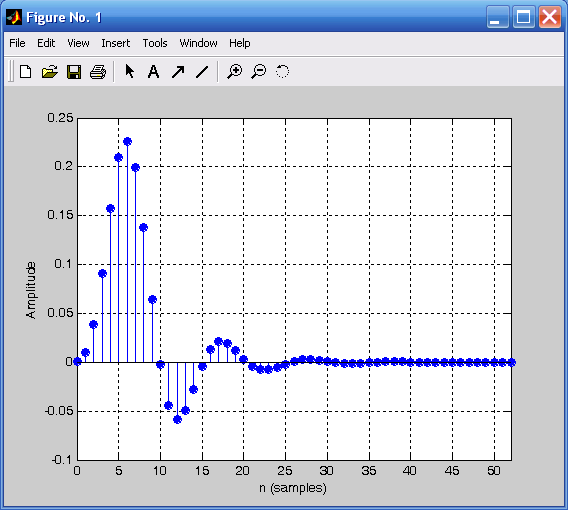
Рис. 8.2. Импульсная характеристика фильтра

В технике часто приходится сглаживать входной сигнал путем определения среднего значения в движущейся системе координат. Если, например, сглаживание осуществляется пятерками, то среднее значение определяется по формуле

, (8.11)

из которой следует, что каждый коэффициент веса равен 0.2.

Используя соотношение (8.11) создадим цифровые фильтры на основе интеграла свертки и блоков задержек.

В m-файле задан дискретный интервал времени и по пяти точкам определен интеграла свертки для входного сигнала, состоящего из двух гармонических сигналов: x₁ и x₂.

t=[0:0.1:1.0]; %Временной интервал входного сигнала

f=0.1; %Частота задающего сигнала

x1=sin(2*pi*f*t); %Задающий сигнал

f1=4; %Частота сигнала помехи

x2=0.2*sin(2*pi*f1*t); %Сигнал помехи

x3=x1+x2 %Сумма сигналов

x22=[1,1,1,1,1,1,1,1,1,1,1]; %Импульсная характеристика фильтра

y1=filter(x3,1,x22)/5 %Выходной сигнал фильтра

figure(3) plot(t,y1,'--',t,x3),grid on.

Результаты представлены на рис. 8.3.

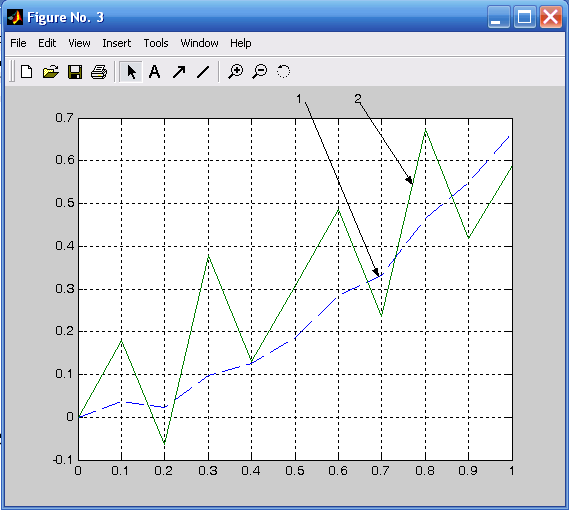
Рис. 8.3. Графики сигналов:

1 – на входе фильтра, 2 – на выходе фильтра

Усреднение группами отсчетов можно выполнить в пакете Simulink, используя блоки задержек (рис. 8.4).

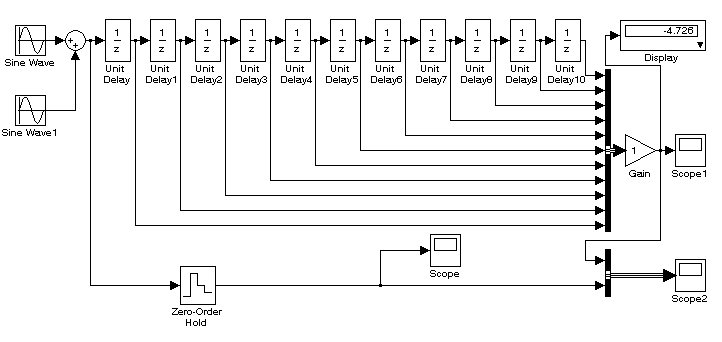
Рис. 8.4. Принципиальная схема фильтра с использованием линий задержек

На вход фильтра, состоящего из одиннадцати блоков задержек, подается полезный сигнал, имитируемый низкочастотным генератором Sine Wave, и сигнал помехи, имитируемый высокочастотным генератором Sine Wave 1 (рис. 8.5). Результаты испытания представлены на рис. 8.6 и 8.7.

Рис. 8.5. Низкочастотный входной сигнал с наложенным сигналом помехи

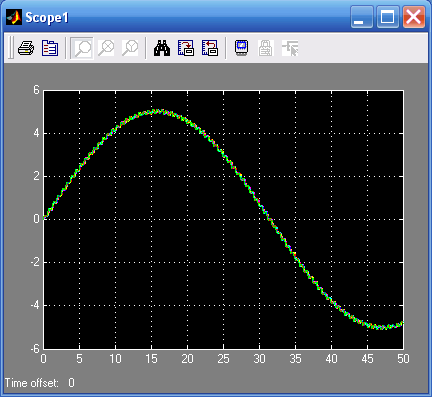
Рис. 8.6. Сигнал, сформированный Рис. 8.7. Сигнал на выходе фильтра

элементами задержек

Задание

1. По заданному вектору входного сигнала и коэффициентам импульсной переходной функции определить выходную последовательность, используя интеграл Дюамеля.

2. По заданному вектору входного сигнала и коэффициентам импульс-ной переходной функции определить выходную последовательность, используя функцию conv.

3. По заданному вектору входного сигнала и коэффициентам импульсной переходной функции определить выходную последовательность, используя filter.

4. По заданному вектору входного сигнала и коэффициентам импульсной переходной функции определить выходную последовательность, исполь-зуя filtfilt.

5. Определить коэффициенты импульсной характеристики по известным коэффициентам передаточных функций.

6. Для заданного входного сигнала написать программу, определяющую параметры фильтра с нулевым фазовым сдвигом.

7. Для заданного входного сигнала написать программу, определяющую параметры фильтра с использованем скользящего среднего.

8. В пакете Simulink составить структурную схему, реализующую фильтр скользящего среднего на линиях задержек.

9. Написать программу для расчета фильтра Баттерворта.

Содержание отчета

1. Листинги программ по расчету выходных сигналов исследуемых фильтров.

2. Анализ результатов расчета дискретных фильтров.

3. Графики.

4. Выводы.

Контрольные вопросы

1. Запишете два варианта интеграла свертки (интеграла Дюамеля) для непрерывной системы.

2. Запишите два варианта числовых последовательностей для дискретных систем, являющихся аналогом интеграла свертки (интеграла Дюамеля).

3. Дайте определение линейного оператора.

4. Поясните свойства принципа суперпозиции и области его применения.

5. Дайте определение стационарной системы, нестационарной системы.

6. В пакете Matlab представьте фрагмент программы, использующий метод импульсной переходной функции для определения параметров дискретного фильтра по его аналоговому эквиваленту.

7. В пакете Matlab представьте фрагмент программы, которая реализует усреднение пятерками в движущей системе координат.

8. Приведите две формы записи аналоговой свертки и сделать пояснения.

9. Приведите две формы дискретной свертки и сделать пояснения.

10. Дайте определение дельта-функции и опишите ее свойства.

11. Дайте определение цифрового единичного импульса и опишите его свойства.

12. Представьте выражение, в котором произвольный аналоговый сигнал определяется через единичные импульсы.

13. Представьте выражение, в котором произвольный дискретный сигнал определяется через единичный цифровой импульс.

Библиографический список

1. Соседка В.Л. Современная теория управления. – Днiпропетровськ: ДНГУ, 2003. – 242 с.

2. Соседка В.Л. Локальные системы автоматики и следящий электропривод. – Днiпропетровськ: ДНГУ, 2004. – 119 с.

3. Половко А.М., Бутусов П.Н. Matlab для студента. – СПб.: БХВ-Петербург, 2005. – 320 с.

4. Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления с примерами на языке Matlab. – СПб.: Наука, 2000. – 475 с.

Содержание

1. Введение в систему Matlab 4

2. Исследование аналого-цифрового преобразователя (АЦП) 15

3. Спектральный и статистический анализ процессов 22

4. Исследование характеристик аналоговых и дискретных фильтров 45

5. Проектирование дискретных фильтров по аналоговому эквиваленту 57

6. Расчет цифровых фильтров с учетом квантования 67

7. Идентификация объектов по кривым разгона 76

8. Изучение алгоритма цифровой свертки 83

Библиографический список

Содержание

98