СИСТЕМЫ И СИГНАЛЫ. МОДЕЛИРОВАНИЕ В MATLAB

Омск

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Омский государственный технический университет»

СИСТЕМЫ И СИГНАЛЫ. МОДЕЛИРОВАНИЕ В MATLAB

Лабораторный практикум

Омск

Издательство ОмГТУ

2009

Составитель:

Шендалева Елена Владимировна, канд. техн. наук

В лабораторном практикуме приведены лабораторные работы по моделированию систем различного вида, идентификации и преобразованию их характеристик в среде пакета прикладного программного обеспечения MATLAB^®.

Лабораторный практикум предназначен для студентов специальности 200503 «Стандартизация и сертификация», изучающих дисциплину «Системный анализ и элементы оптимизации».

Печатается по решению редакционно-издательского совета

Омского государственного технического университета.

Лабораторные работы выполняют в среде программного пакета MATLAB^ 6.5. Matlab – система многоцелевого назначения, первоначальную основу которой составляли алгоритмы решения систем линейных уравнений и задач, откуда и произошло ее название «матричная лаборатория». В настоящее время в среде Matlab моделируют разнообразные типы систем, решают вопросы их оптимизации, идентификации, преобразования, взаимодействия и определения различных характеристик.

Лабораторная работа № 1 Введение в среду Matlab

Цель работы

1. Освоение работы в среде программного пакета Matlab.

2. Освоение стандартных программных структур и команд: чисел, матриц, функций, действий с массивами чисел.

Теоретическое обоснование

Среда Matlab реализована на языке C и включает интерпретатор команд на языке высокого уровня, графическую систему, пакеты расширений. Вся работа организуется через командное окно (Command Window), которое появляется при запуске программы matlab.exe. В процессе работы данные располагаются в памяти (Workspace); для изображения кривых, поверхностей и других графиков создаются графические окна.

В командном окне в режиме диалога проводятся вычисления. Пользователь вводит команды или запускает на выполнение файлы с текстами на языке Matlab. Интерпретатор обрабатывает введенное и выдает результаты: числовые и строковые данные, предупреждения и сообщения об ошибках. Строка ввода помечена знаком >>.

Все значения переменных, вычисленные в течение текущего сеанса работы, сохраняются в зарезервированной области памяти компьютера, называемой рабочим пространством системы Matlab (Workspace). Командой clc можно стереть содержимое командного окна, но это не затронет содержимого рабочего пространства. Когда исчезает необходимость в хранении переменных в текущем сеансе работы, их можно стереть из памяти компьютера командой clear или clear(имя1,имя2). Первая команда удаляет из памяти все переменные, а вторая – переменные с именами имя1 и имя2. Командой who можно вывести список всех переменных, входящих в данный момент в рабочее пространство системы. Для просмотра значения любой переменной из текущего рабочего пространства системы необходимо набрать ее имя и нажать клавишу Enter.

Чтобы сохранить в файле на диске компьютера содержимое рабочего пространства системы Matlab, нужно выполнить команду меню File/Save Workspace As. По умолчанию расширение имени файла mat, поэтому такие файлы принято называть mat-файлами. Для загрузки в память компьютера ранее сохраненного на диске рабочего пространства нужно выполнить команду меню File/Load Workspace.

Описание работы

Основной тип данных double задает действительные числа мантиссой и показателем степени. По умолчанию используется формат short, при котором показываются только четыре десятичных цифры после запятой.

res=4.234*1.757/3.14-69.344+10.274

res = -56.7008.

В формате double:

format long

res

-56.70084777070063.

Для возвращения к старой точности визуального представления вещественных чисел в командном окне

format short.

Над вещественными и комплексными числами и переменными производятся операции: сложения +, вычитания –, умножения *, деления / и возведения в степень ^. Список всех имеющихся в системе элементарных математических функций может быть получен по команде help elfun.

Если нет необходимости видеть в командном окне результат вычисления, то в конце введенного выражения следует поставить точку с запятой и только после этого нажать Enter.

Вычислите выражение, включающее вычисление функции арксинус:

2*asin(1).

ans = 3.1416,

что соответствует числу π, также обозначаемому в Matlab pi.

В Matlab есть логические функции и функции, связанные с целочисленной арифметикой (округление до целого round, усечение дробной части fix).

Помимо арифметических операций над операндами типа double выполняются еще операции сравнения операндов по величине. Эти операции записываются знаками (табл. 1.1).

Таблица 1.1.

Символьные обозначения операций отношения

Меньше	Меньше или равно	Больше	Больше или равно	Не равно	Равно
<	<=	>	>=	~=	==

В случае истинности операции ее результат равен 1, в случае ложности – 0. Данные операции имеют более низкий приоритет, чем арифметические.

a=2; b=4; c=3;

res=(a<b)+(c==b)+(b~=a)

res=2.

Комплексные и вещественные переменные автоматически имеют тип double. Для записи мнимой единицы зарезервированы буквы i или j. В случае, когда коэффициентом перед мнимой единицей является не число, а переменная, между ними следует обязательно использовать знак умножения.

5+3i

-4.897+0.725e-3*i

4-7j

syms x y;x+y*i.

Почти все элементарные функции допускают вычисления с комплексными аргументами:

res=sin(5+3i)*atan(8i)/(2-5i)

-1.6309 - 2.4520i.

Для работы с комплексными числами используют функции: abs (абсолютное значение комплексного числа), conj (комплексно сопряженное число), imag (мнимая часть комплексного числа), real (действительная часть комплексного числа), angle (аргумент комплексного числа), isreal («истина», если число действительное). Также используют функции отношений:

c=2+2i;d=3i;

c>d

Для создания одномерного массива можно использовать операцию конкатенации, обозначаемую с помощью скобок [ ]. Элементы массива помещают между скобками и отделяют друг от друга пробелом или запятой:

al=[1 2 3]; d=[1+2i,2+3i,3-7i].

Для доступа к элементу массива необходимо применить операцию индексации – после имени массива указать в круглых скобках индекс элемента.

Можно изменить элементы уже сформированного массива путем применения операций индексации и присваивания:

al(3)=664

или сочетания операции присваивания и преобразования:

al(2)=(al(1)+al(3))/2.

Возможно добавление элемента к уже существующему массиву:

al(4)=7.

Число элементов массива получают с помощью функции length:

length(al)

ans = 4.

Удлинение массива а1 можно выполнить с помощью конкатенации:

al=[al 7].

Можно задать массив, прописывая все его элементы по отдельности:

a3(1)=67; a3(2)=7.8; a3(3)=0.017.

Для формирования диапазона числовых значений через двоеточие следует набрать первое число диапазона, шаг и конечное число диапазона:

diap=3.7:0.3:8.974.

Для создания двумерного массива (матрицы) используют операцию конкатенацию. Элементы массива набирают согласно их расположению в строках, в качестве разделителя строк используют точку с запятой:

a=[1 2; 3 4; 5 6]

a =

1 2

3 4

5 6.

Матрицу а размером 3  2 (число строк  число столбцов) можно сформировать с помощью вертикальной конкатенации векторов-строк:

a=[[1 2];[3 4];[5 6]]

или с помощью горизонтальной конкатенации векторов-столбцов:

a=[[1;3;5],[2;4;6]].

Структуру созданных массивов можно узнать с помощью команды whos(имя массива), размерность массива – ndims, а размер массива – size.

Двумерные массивы также задают с помощью операции индексации. Номера строки и столбца, на пересечении которых находится задаваемый элемент массива, указывают через запятую в круглых скобках:

a(1,1)=1; a(1,2)=2; a(2,1)=3;

a(2,2)=4; a(3,1)=5; a(3,2)=6.

Однако будет эффективнее до начала прописывания элементов массива создать массив нужного размера функциями ones(m,n) или zeros(m,n), заполненный единицами или нулями (m – число строк, n – число столбцов).

Поменять местами строки матрицы с ее столбцам можно операцией транспортирования (.') (точка и апостроф):

A=[1 1 1; 2 2 2; 3 3 3];

B=A.'

B = 1 2 3

1 2 3

1 2 3.

Операции сложения и вычитания матриц обозначают знаками + и –:

A=[1 1 1; 2 2 2; 3 3 3]; B=[0 0 0; 7 7 7; 1 2 3]; A+B.

При выполнении операции А + скаляр система расширит скаляр до массива размера А, который и складывается поэлементно с А.

A+5

ans = 6 6 6

7 7 7

8 8 8.

Для поэлементного перемножения, деления и возведения в степень массивов применяют операции, обозначаемые символами (.*), (./), и (.^).

Кроме операции правого поэлементного деления ./ существует операция левого поэлементного деления .\. Выражение А./В приводит к матрице с элементами А(k,m)/В(k,m), а выражение А.\В приводит к матрице с элементами В(k,m)/А(k,m).

Знаки * и \ закреплены за перемножением и делением матриц и векторов в задачах линейной алгебры.

Задачи, связанные с нахождением длин векторов и углов между ними с вычислением скалярного и векторного произведений, легко решаются средствами Matlab. Нахождение векторного произведения:

u=[3 1 2]; v=[3 2 1];

cross(u,v)

ans =

-3 3 3.

Нахождение скалярного произведения:

sum(u.*v) или u*v'.

Длину вектора вычисляют как

sqrt(sum(u.*u)).

Для задания специальных матриц используют функцию создания единичной матрицы eye и функцию rand, генерирующую массив со случайными элементами, равномерно распределенными на интервале от 0 до 1. Например, R=rand(3)порождает массив размером 3  3. Если аргументов два, например R=rand(2,3), то матрица R имеет размер 2  3. Если аргументов три и более, то создаются многомерные массивы случайных чисел.

Определитель квадратной матрицы вычисляют с помощью функции det. Среди функций, производящих вычисления над массивами, помимо функции sum существует функция prod, которая вычисляет произведение элементов. Функции max и min определяют максимальный и минимальный элементы массивов. Для векторов – это единственное числовое значение, а для матриц – набор элементов, вычисленных для каждого столбца.

Matlab дает возможность производить групповые вычисления над массивами, используя обычные математические функции. С помощью компактных записей в интерактивном режиме работы удается произвести большой объем вычислений. Например, всего два коротких выражения

x=0:0.01:pi/2; y=sin(x)

формируют два вектора X и Y со 158 элементами каждый.

Графические возможности Matlab разнообразны. Графические объекты показываются в специальных окнах, имеющих в заголовке слово Figure.

Сформируем векторы X и Y и вызовем функцию plot (рис.1.1):

x=0:0.01:2; y=sin(x);

plot(x,y).

Не убирая с экрана первое графическое окно введем:

z=cos(x);

plot(x,z)

и получим новый график в том же самом графическом окне (рис. 1.2).

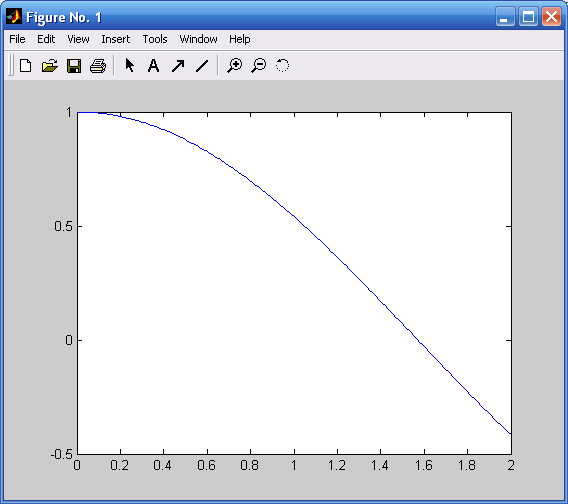
Рис. 1.1. График функции y=sin(x) Рис. 1.2. График функции z=cos(x)

Если необходимо оба графика разместить в одном окне, то выполним:

x=0:0.01:2; y=sin(x); plot(x,y)

z=cos(x);

hold on

plot(x,z).

Практически то же самое получится (рис. 1.3), если набрать:

x=0:0.01:2; y=sin(x); z=cos(x);

plot(x,y,x,z).

Если нужно показать несколько графиков, то это можно сделать двумя способами: а) построить их в разных графических окнах дополнительной командой figure; б) разбить область вывода графической информации на несколько подобластей (subplot), в каждую из которых можно вывести графики различных функций.

Например, для функций sin и cos разместим графики в первой подобласти, а график функции exp(х) – во второй подобласти одного окна (рис. 1.4):

w=exp(x);

subplot(1,2,1); plot(x,y,x,z)

subplot(1,2,2); plot(x,w).

Первый аргумент функции subplot равен числу рядов подобластей, второй – числу колонок подобластей, а третий – номеру подобласти. Снять действие функции subplot можно командой

subplot(1,1,1).

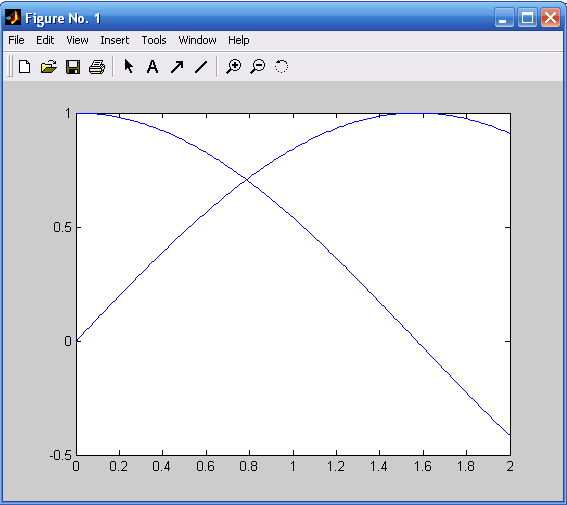
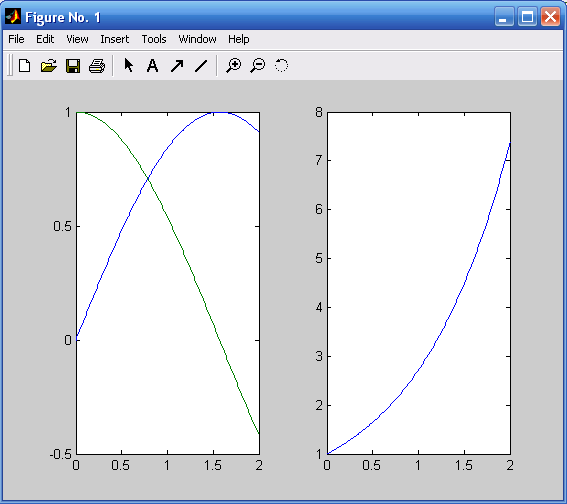
Рис. 1.3. Графики функций y=sin(x), z=cos(x), Рис. 1.4. Графики функций y=sin(x), z=cos(x)

построенные в одном графическом окне и w=exp(x), построенные в двух подобластях

одного графического окна

График функции можно построить в полярных координатах (рис. 1.5):

phi=0:0.01:2*pi; r=sin(3*phi);

polar(phi,r).

В Matlab существуют возможности управления внешним видом графиков – заданием цвета и стиля линий, размещением надписей. Например,

x=0:0.1:3; y=sin(x);

plot(x,y,'g-',x,y,'k*')

позволяет задать график в виде сплошной линии (рис. 1.6), на которой в вычисляемых точках проставляют черные звездочки.

В общем случае функция plot(x1, y1, s1, x2, y2, s2) позволяет объединить в одном графическом окне несколько графиков функций y₁(x₁), y₂(x₂) с индивидуальными стилями s₁, s₂. Стили задают в виде набора трех символьных маркеров, заключенных в одиночные кавычки (апострофы). Один из этих маркеров задает тип линии (табл. 1.2), другой маркер задает цвет (табл. 1.3), третий – тип проставляемых «точек» (табл. 1.4).

Таблица 1.2

Маркеры, задающие тип линии

Маркер	-	--	:	-.
Тип линии	Непрерывная	Штриховая	Пунктирная	Штрихпунктирная

Таблица 1.3

Маркеры, задающие цвет линии

Маркер	Цвет линии	Маркер	Цвет линии
c	голубой	g	зеленый
m	фиолетовый	b	синий
y	желтый	w	белый
r	красный	k	черный

Таблица 1.4

Маркеры, задающие тип точки

Маркер		+	*		
Тип точки	точка	плюс	звездочка	кружок	крестик

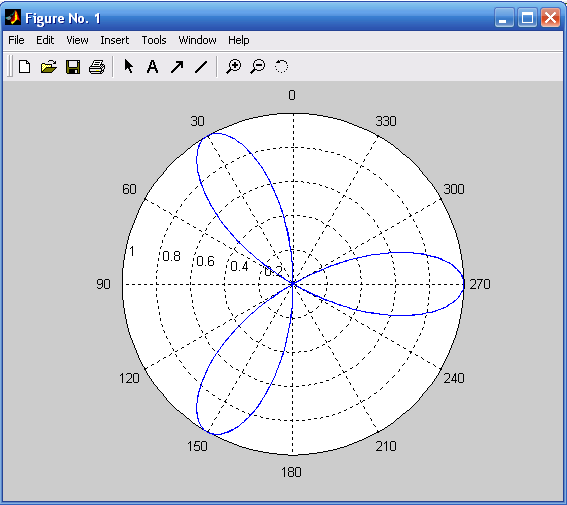
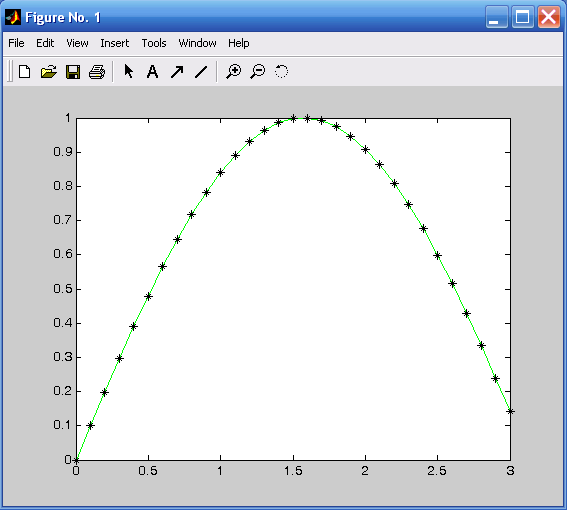
Рис. 1.5. График функции r=sin(3*phi) Рис. 1.6. Построение графика функции

в полярных координатах y=sin(x) в двух разных стилях

При оформлении осей координат масштабы устанавливаются автоматически. Задание своих пределов изменения переменных по осям координат осуществляется с помощью функции axis([xmin,xmax,ymin,ymax]).

Для проставления различных надписей на полученном рисунке применяют функции xlabеl, ylabеl, title и text. Функция xlabеl создает подпись у горизонтальной оси, функция ylabеl – у вертикальной оси. Функция text размещает надпись на рисунке. Общий заголовок создает функция title. Функция grid on наносит измерительную сетку на область построения графика. Например (рис. 1.7):

x=0:0.1:3; y=sin(x);

plot(x,y,'g-',x,y,'k*')

title('Function sin(x) graph');

xlabel('xcoordinate'); ylabel('sin(x)');

text(2.1, 0.9, '\leftarrowsin(x)'); grid on.

С помощью функции text надпись помещают в точке с координатами, указанными первыми двумя аргументами.

Matlab позволяет отображать трехмерные графические объекты. Каждая точка в пространстве характеризуется тремя координатами. Набор точек, принадлежащих некоторой линии в пространстве, задают в виде трех векторов. После чего с помощью функции plot3 эти векторы будут использованы для построения трехмерной линии (рис. 1.8).

t=0:pi/50:10*pi;

x=sin(t);

y=cos(t); plot3(x,y,t); grid on.

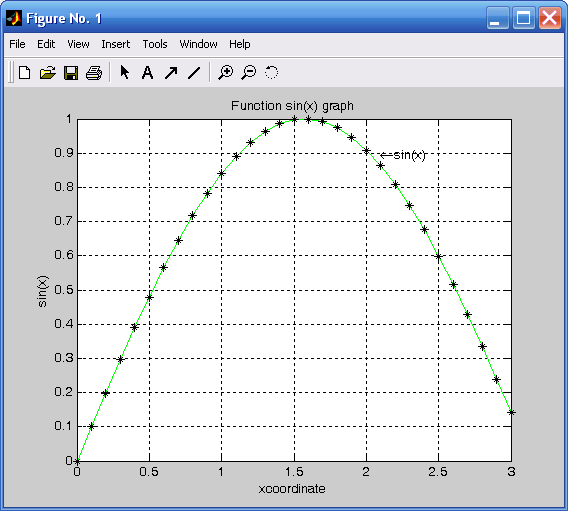
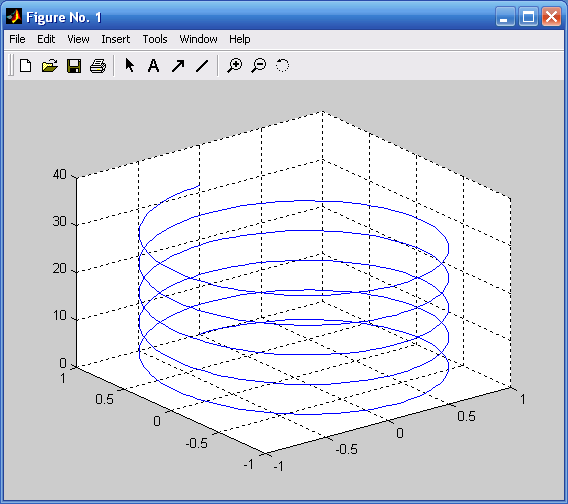
Рис. 1.7. График функции y=sin(x) с надписями Рис. 1.8. График винтовой линии, построенный

на координатных осях и на рисунке с помощью функции plot3

Эту же функцию plot3 можно применить и для изображения поверхностей в виде набора линий в пространстве (рис. 1.9):

[x,y]=meshgrid([-2:0.1:2],[-2:0.01:2]); %Задание узлов сетки

z=exp(-x.^2-y.^2); %Задание трехмерной экспоненты

plot3(x,y,z) %Формирование трехмерной поверхности.

Функции mesh(x,y,z,c), mesh(z,c), mesh(z) определяют задание сетчатой поверхности (массив с определяет цвета узлов поверхности), рис. 1.10, 1.11. Если x, y не указаны, то x=1:n, y=1:m, где [m,n]=size(z).

[x,y]=meshgrid(-8:0.5:8); %Задание узлов сетки x и y

t=sqrt(x.^2+y.^2)+0.001; %Задание аргумента в узлах сетки

z=sin(t)./t; %Расчет функции двух аргументов

mesh(x,y,z) %Построение поверхности.

Функция meshс в дополнение к поверхности строит проекции линий уровня, а meshz делает срез поверхности до нулевого уровня (пьедестал)

meshc(x,y,z) %Рис. 1.11

meshz(x,y,z) %Рис. 1.12.

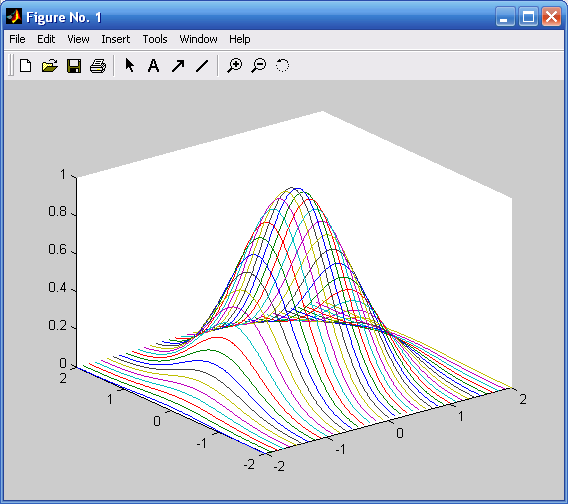
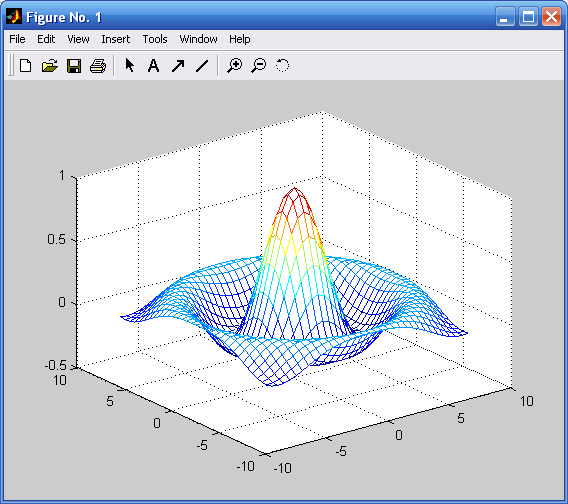
Рис. 1.9. График поверхности в пространстве, Рис. 1.10. График поверхности в пространстве,

построенный с помощью функции plot3 построенный с помощью функции mesh

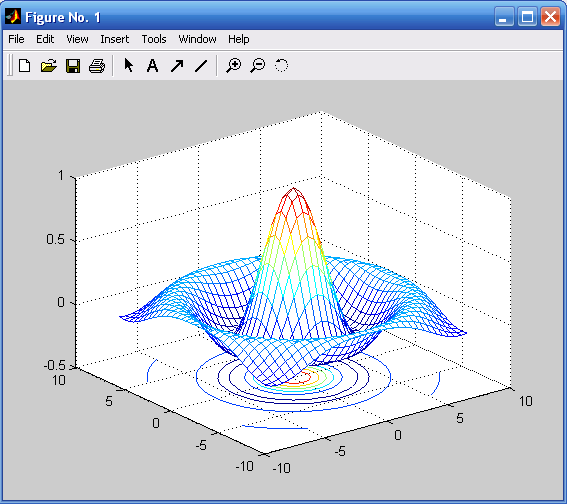
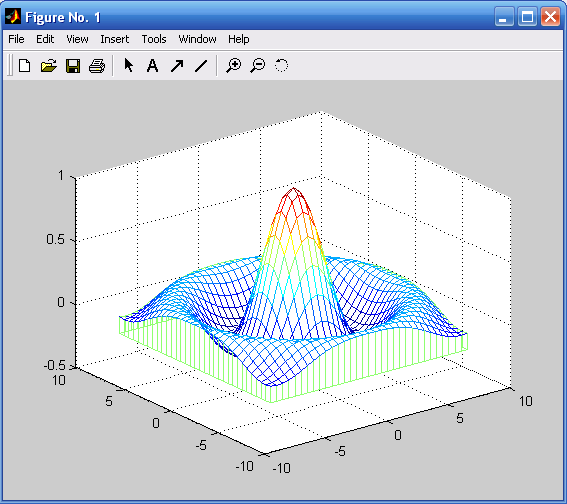
Рис. 1.11. График поверхности в пространстве, Рис. 1.12. График поверхности в пространстве,

построенный с помощью функции meshc построенный с помощью функции meshz

Задание

1. Разобрать приведенные примеры в Matlab.

2. В соответствии с индивидуальным вариантом задать матрицу А с помощью операции конкатенации:

.

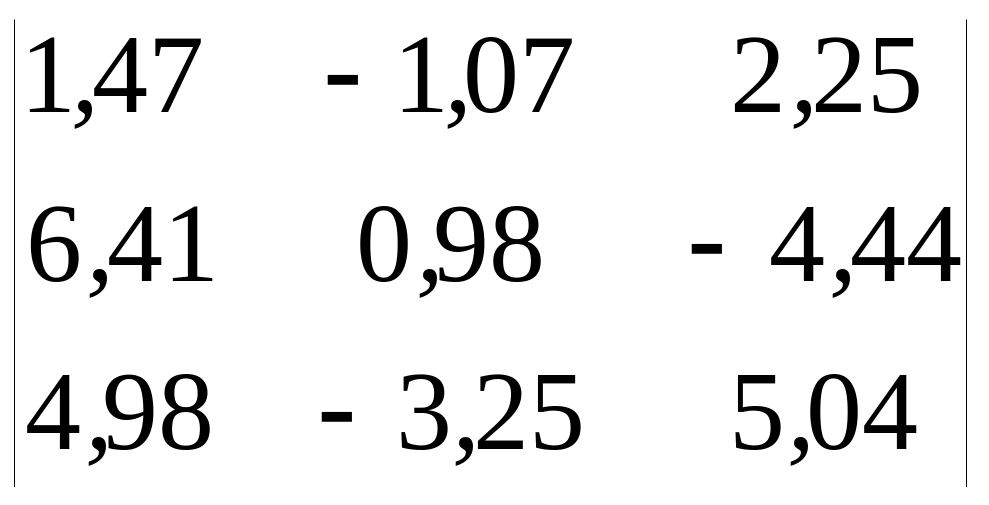3. Сгенерировать массив В размером 3  3 со случайными элементами, равномерно распределенными на интервале от 0 до 1.

4. Выполнить действия:

– преобразовать матрицы: A + 10  B, A  B, B^T;

– почленно умножить А на В;

– расположить элементы матрицы А по возрастанию (по столбцам);

– определить максимальный и минимальный элементы матрицы В;

– вычислить определитель матрицы В.

5. Задать массив С, используя операцию индексации и одну из функций: ones или zeros:

.

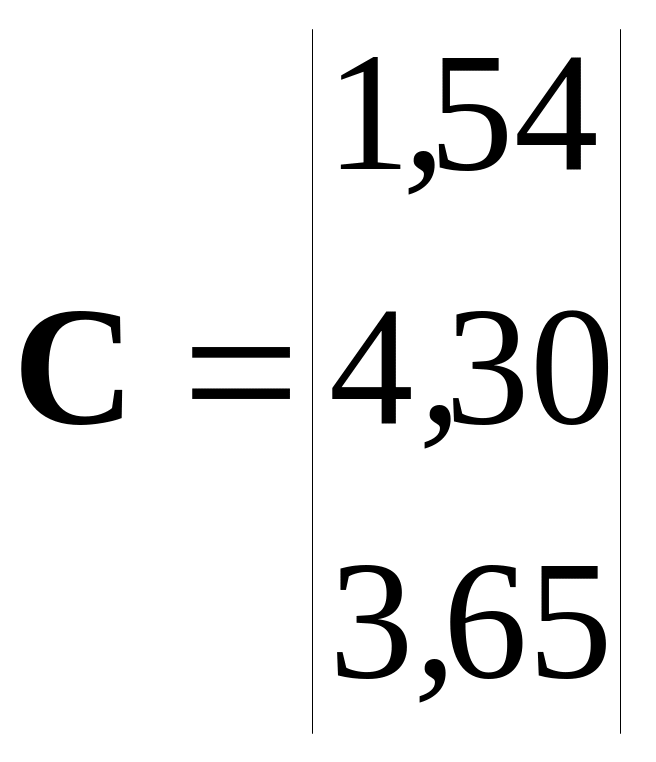6. Решить систему алгебраических линейных уравнений:

A  X = C.

7. Определить массив D:

.

8. Для двух векторов:

и

определить:

; ; .

9. Построить два графика в рамках одних осей координат:

, , .

Сделать надписи на осях, заголовок для графика, пояснительную надпись на рисунке. Задайте самостоятельно тип линий и цвет.

10. Построить графики функций y(x) и z(x) в разных подобластях одного графического окна.

11. Построить поверхность:

, .

Содержание отчета

1. Листинги выполнения заданий.

2. Графики функций в соответствии с заданием.

Контрольные вопросы

1. Как изменить на экране формат вывода числа?

2. Как можно просмотреть в Matlab список всех элементарных математических функций?

3. Какие виды функций в Matlab Вам известны?

4. Опишите способы создания одномерных массивов в Matlab.

5. Опишите способы создания двумерных массивов в Matlab.

6. Перечислите и объясните действие операторов, используемых при вычислениях с массивами.

7. Опишите действие операций отношения.

8. Как построить декартовый и полярный графики функции одной переменной?

9. Как построить несколько графиков в одной системе координат?

10. Как построить графики в разных подобластях одного графического окна?

11. Как изменить цвет и стиль линий на графиках?

12. Как сделать надписи на осях, на полученном рисунке? Как сделать заголовок для графика?

13. Как построить график функции двух переменных? Как построить график поверхности?

14. Что такое m-файлы? Как создать, сохранить и вызвать m-файл?