
 формуласы
нені есептейді?+Сызықтық
үлестірім дисперсиясын
формуласы
нені есептейді?+Сызықтық
үлестірім дисперсиясын
 нені
есептейді? + Гамма
үлестірім дисперсиясын
нені
есептейді? + Гамма
үлестірім дисперсиясын
 нені
есептейді?+ Сызықтық
үлестірімнің тығыздығын
нені
есептейді?+ Сызықтық
үлестірімнің тығыздығын
 формуласы
қандай аралықтағы сандарды
модельдеугеқолданылады: +(0,
m)интервалында
бірқапыпты үлестірілген кездейсоқ
сандарды.
формуласы
қандай аралықтағы сандарды
модельдеугеқолданылады: +(0,
m)интервалында
бірқапыпты үлестірілген кездейсоқ
сандарды.
 формуласы
нені есептейді? +Гамма
үлестірімнің математикалық үмітін
формуласы
нені есептейді? +Гамма
үлестірімнің математикалық үмітін
 формуласының
нені есептейтіндігін анықта:+Қалыпты
үлестірімнің математикалық үмітін
формуласының
нені есептейтіндігін анықта:+Қалыпты
үлестірімнің математикалық үмітін
"шығарып тастау" әдісін кім шағарған?+Джон Фон Нейман
.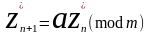 өрнегінің
параметрлерін таңдау қандай шартпен
анықталады? +
өрнегінің
параметрлерін таңдау қандай шартпен
анықталады? +  -кез-келген оң, тақ, бүтін сан; а
= 8t±3,
мұнда t-
кез-келген
оң сан,
-кез-келген оң, тақ, бүтін сан; а
= 8t±3,
мұнда t-
кез-келген
оң сан,
 ,мұнда
b-
машиналық
сөздегі екілік цифрлардың саны.
,мұнда
b-
машиналық
сөздегі екілік цифрлардың саны.
+ Бірқалыпты
2 орынды кездейсоқ санды rand функциясы арқылы қалай алуға болады? +round(10^2*rand(1,1))
215*2(mod4) неге тең ? +2
3 орынды кездейсоқ санды rand функциясы арқылы қалай алуға болады? +round(10^3*rand(1,1))
397 * 7 (mod 8) неге тең: +3
4 орынды кездейсоқ санды rand функциясы арқылы қалай алуға болады? +round(10^4*rand(1,1))
4-ші 5-ші ретті Рунге-Кутта әдісі бойынша қарапайым дифференциалдық теңдеулерді шешетін функция: + ode45
4-ші
5-ші ретті Рунге-Кутта әдісі бойынша
қарапайым дифференциалдық теңдеулерді
шешуші ?+
5 орынды кездейсоқ санды rand функциясы арқылы қалай алуға
болады? +round(10^5*rand(1,1))
fffffffffffffffffffffff
 формуласы
нені анықтайды:+Гамма
үлестірімнің тығыздық функциясы
формуласы
нені анықтайды:+Гамма
үлестірімнің тығыздық функциясы
f(х1, х2, ,, хп)тығыздық функциясымен берілген n-өлшемдіη = (η1¸ η2 ¸¸ ηn) кездейсоқ шаманы модельдеу, осы векторлык шаманы кұраушы скалярлы ηi, і =,…,nкездейсоқ шамалардъщ бірінен соң бірінің нақтыламалырын табуға әкеледі. Бұл - +Тізбектеп модельдеу әдісі
f(х1, х2, ,, хп)тығыздық функциясымен берілген n-өлшемдіη = (η1¸ η2 ¸¸ ηn) кездейсоқ шаманы модельдеу, осы векторлык шаманы кұраушы скалярлы ηi, і =1,…,nкездейсоқ шамалардъщ бірінен соң бірінің нақтыламалырын табуға әкеледі. Бұл -+Тізбектеп модельдеу әдісі
ƒη (x1, x2,…,xn)= ƒ1(x1)*ƒ2(x2/x1)*…* ƒn(xn/ x1…xn-1) өрнегінің оң жағындағы шартты тығыздық функциялары қалай анықталады:+ ƒ1(x1) = ∫…∫ ƒη (x1,…,xn)dx2…dxn;
ƒη (x1, x2,…,xn)= ƒ1(x1)*ƒ2(x2/x1)*…* ƒn(xn/ x1…xn-1) өрнегінің оң жағындағы шартты тығыздық функциялары келесі теңдеулер жүйесімен анықталады:+ ƒ1(x1) = ∫…∫ ƒη (x1,…,xn)dx2…dxn;ƒ2(x2/x1) = ∫…∫ƒn(x1,…,xn)dx3…dxn*(ƒ1(xi))-1; ……… ƒn(xn/ x1…xn-1) = ∫…∫ƒn(x1,…,xn)/ ƒ1(x1) *… … ƒη-1(xη-1/x1xn-2)
MMMMMMMMMMMM
MatLab жүйесі. Меншіктеу операторы:+=
MatLab жүйесі. Циклдық оператордың жазылуы:+ for……..end
MatLab жүйесі.grid операторының қызметі + Тор (сетка) сызады
MatLab жүйесі.ode45 мағнасы:+Функция аты
MatLab жүйесі – бұл ? +Инженерлік, ғылыми есептеулер мен графиктерді өңдеуге арналған компьтерлік математика
MatLab жүйесінде орындалатын есептеулер:+Барлық жауап дұрыс
MatLab
жүйесінің командалық жол көрінісі:
MatLab жүйесінің сипаттамасы: +Инженерлік, ғылыми есептеулер мен графиктерді өңдеуге арналған компьтерлік математика
MatLab. M-файл сипаттамасы: +Дискіде сақталатын MatLab командалар жиыны
MatLab. Команда нәтижесі бірден экранға шықпайды?+Команданы нүктелі үтірмен аяқтап enter пернесін басқанда
MatLab. Редакциялау алаңы деген не?+Бұкіл жұмыс кеңістігі
MatLab.M-файлды
жүктеу командасы? +
MatLab.Команда нәтижесін экранға шығару үшін: +Командадан кейін enter пернесін басу жеткілікті
MatLabжүйесі қандай есептеулерді жүзеге асырады? +Барлық жауап дұрыс
MatLabжүйесі.Массивтер мен векторларды элемент бойынша бөлу: +./
MatLabжүйесі.Массивтер мен векторларды элемент бойынша көбейту: +.*
MatLab-та M-файл деген не? +Дискіде сақталатын MatLab командалар жиыны
MatLab-та
M-файлды шақыру командасы ? +
mod(a,b) функциясы: +a-ны b-ға бөліп қалдығын қайтарады
OOOOOOOOOO
ode45 қандай әдіске негізделген?+Рунге-Кутта әдісіне
ode45 қарапайым дифференциалдық теңдеулерді шешушіқандай әдіске негізделген? +Рунге-Кутта әдісіне
ode45 қарапайым дифференциалдық теңдеулерді шешушінегізделген әдіс: +Рунге-Кутта әдісіне
ode45 қарапайым дифференциалдық теңдеулерді шешушіфункция қандай әдіске негізделген? +Рунге-Кутта әдісіне
pppppppppppp
Pυ=k}= e-λПуассон
формуласындағы λ нені анықтайды:+Уақыт
бірлігіндегі оқиғалар санының орта
мәні
e-λПуассон
формуласындағы λ нені анықтайды:+Уақыт
бірлігіндегі оқиғалар санының орта
мәні
RRRRRRRRRRRRRRR
Rand (30,1) функциясының нәтижесі +(0,1) аралығынан 30 кездейсоқ санды береді
Rand функциясы қандай сандар аралығында жұмыс жасайды? +(0,1)
rand функциясы қандай сандарды генерациялайды? +Кездейсоқ сандарды
rand функциясы қандай үлестірімділік заңдылығымен берілген кездейсоқ сандарды генерациялайды?
rand(300,1) функциясының нәтижесі + (0,1) аралығынан 300 кездейсоқ санды береді
rand(50,1) функциясының нәтижесі + (0,1) аралығынан 50 кездейсоқ санды береді
rand(500,1) функциясының нәтижесі +(0,1) аралығынан 500 кездейсоқ санды береді
randфункциясы генерациялайды:+Кездейсоқ сандарды
randфункциясы қандай сандарды генерациялайды? +Бірқалыпты үлестірілген кездейсоқ сандарды
randфункциясының анықталу облысы: +(0,1)
XXXXXXXX
x-ты y-қа бөліп қалдығын қайтаратын функция: +mod(x,y)
ZZZZZZZZZZZ
z*n+1 =az*nформуласы нені есептейді:+базалық тізбектің жаңа нақтыламасын
z=0.14
болғанда
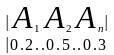 толық
топ оқиғасының модельдеу нәтижесін
табыңыз. +
толық
топ оқиғасының модельдеу нәтижесін
табыңыз. + оқиғасы.
оқиғасы.
z=0.14 болғанда толық топ оқиғасының модельдеу нәтижесінтабыңыз. + оқиғасы.
z=0.54
болғанда -
түрінде берілтен толық топты оқиғаны
модельдеудіңнәтижесін табыңыз.
+
-
түрінде берілтен толық топты оқиғаны
модельдеудіңнәтижесін табыңыз.
+  оқиғасы.
оқиғасы.
z0 = 0,5156 болсын. Келесі жуықтау z1=0,5843 қандай әдіспен алынған? +Орташа шаршы
z0 = 0,5556 менz1= 0,8691 болсын. Келесі жуықтау z2=0,2871 қандай әдіспен алынған?+ Орташа көбейту
Z0=0,2531 мәні арқылы орташа шаршы әдісімен келесі жуықтауды табыңыз: +Z1 =0,4059
Z0=0,7214 Z1= 0,2573 мәндері арқылы орташа көбейту әдісімен келесі жуықтауды табыңыз:+Z2=0,5616
zо= 0,5556 болса, к неге тең:+2
өрнегі бойынша алынған кездейсоқ сандар тізбегінің периоды Р=m болу үшін қандай шарттар орындалуы тиіс? +с және т - өзара жай сандар; (а-1)саны 4-ке еселі, егер т саны да төртке еселіболса және - (0, m)интервалындағы кез-келген оң, бүтін сан
өрнегі бойынша алынған кездейсоқ сандар тізбегінің периоды Р=m болу үшін қандай шарттар орындалуы тиіс?+ с және т - өзара жай сандар; (а-1)саны 4-ке еселі, егер т саны да төртке еселі болса және -(0, m)интервалындағы кез-келген оң, бүтін сан.
формуласы қандай аралықтағы сандарды модельдеугеқолданылады:+ (0, m)интервалында бірқалыпты үлестірілген кездейсоқ сандарды.
формуласы қандай аралықтағы сандарды модельдеугеқолданылады:+ (0, m)интервалында бірқапыпты үлестірілген кездейсоқ сандарды.
формуласы қандай аралықтағы сандарды модельдеугеқолданылады: + (0, m)интервалында бірқапыпты үлестірілген кездейсоқ сандарды.
 формуласы
қандай сандарды моделъдеугеқолданылады?+Кездейсоқ
үздіксіз шамаларды.
формуласы
қандай сандарды моделъдеугеқолданылады?+Кездейсоқ
үздіксіз шамаларды.
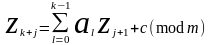 формуласы
қандай аралықтағы сандарды модельдеуге
қолданылады? +(0,
m)
интервалында
бірқалыпты
үлестірілген
кездейсоқ
сандарды.
формуласы
қандай аралықтағы сандарды модельдеуге
қолданылады? +(0,
m)
интервалында
бірқалыпты
үлестірілген
кездейсоқ
сандарды.
 формуласы
қандай
аралықтағы
сандарды
модельдеуге
қолданылады?+ (0,1)
интервалында
сызықты
үлестірілген
кездейсоқ
сандарды.
формуласы
қандай
аралықтағы
сандарды
модельдеуге
қолданылады?+ (0,1)
интервалында
сызықты
үлестірілген
кездейсоқ
сандарды.
формуласықандайсандардымоделъдеугеқолданылады?+ Кездейсоқ үздіксіз шамаларды.
шегерінді
әдісі мына түрде есептеледі:+ 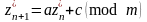
η η η η η η η η η η η
η және τ кездейсоқ шамаларының нақтыламаларын сәйкесінше х және y арқылы белгілеп, η = (η1¸¸ ηn) векторлық кездейсоқ шамаларды модельдейтін нақты формулаларды жазуға болады:+ X1=m1+ a11 y1
η кездейсоқ векторын η = т + Аτтүрлендіруімен алуға болады. Мұндағы τ кұраушылары дегеніміз не? +(τi) мөлшерленген қалыпты үлестірім заңына бағынышты векторы кездейсоқ шама
ξξξξξξξξξξξξ
ξкездейсоқ
шамасының дисперсиясы:+
ξкездейсоқ
шамасының математикалық үміті мынаған
тең:+ 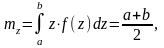
ξкездейсоқ
шамасының орта квадраттық ауытқуы
мынаған тең:+ 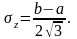
ξкездейсоқ
шамасының тағы бір сипаттамасы болатын
үлестірім функциясы былай есептеледі+
AAAAAAAAAAAAAAAAAAA
Айнымалы tni - +і-ші тауарды әкелу күні
Айнымалы vi– +і-ші тауардың қоймадағы кор деңгейі
Айнымалы VPn, VPni – +толык және әр тауарға тапсырыстарды ұйымдастыруға шығындар
Айнымалы vmini vpmi- + і-ші тауар корының шектілік және шектілік алдындағы денгейі
Айнымалы VР - +толық шығындар
Айнымалы VРХ , VРxі – +толық және әр тауардың қорын сақтауға шығындар
Аналитикалық модельдердің компьютерлік модельдерден айырмашылығын көрсетіңіз: +компьютер құралдарын қолданбайтын математикалық модельдер
Аналитикалық модельдің компьютерлік модельден айырмашылығы: +компьютер құралдарын қолданбайтын математикалық модельдер
Аялдамаға келетін автобус сіз күткен маршруттікі болу ықтималдылығы р-ға тең. Сіздің автобусыңыз нешінші болатынын аныктаңыз. Мұнда қандай үлестірім заңдылығын қолдану керек? + Геометриялық.
ӘӘӘӘӘӘӘӘӘӘӘӘ
Әр қайсысы кез келген мезгілде орындалатын оқиғалар санымен сипатталатын үлестірім қандай?+ Пуассон үлестір імін
әрбір ηiкездейсоқ шамасын бір-біріне тәуелсіз модельдеуге болады, мысалы, кері функция әдісімен:+ηi=F-1(ζi), i=1,2,…,n
Әрбір серияның ішінде өткізілетін сынақ санын мына формуламен табамыз:+n= λ/p
Әрбір серияның ішінде өткізілетін сынақ санына сәйкес формуланы табамыз: +п = λ/p
базалық кездейсоқ сандардың тізбегі ретінде, (0, 1) кесінді аралығында бірқалыпты үлестірілген, ξ кездейсоқ шамасының zi нактыламаларының тізбегін таңдап алу келесі факторға негізделеді:+ Бірқалыпты үлестірім кездейсоқ заңдылыктардың ең қарапайымы болғандықтан оны оңай математикалық түрлендіруге болады
Ббббббббббббббббббббббб
Байланыс
каналының екі күйі бар:
 - бос;
- бос;
 -
бос емес. Келесі мәндердегі марков
тізбегін табыңыз: +
-
бос емес. Келесі мәндердегі марков
тізбегін табыңыз: +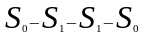
Берілген z= 0,6 бойынша P(η≤x)= (2х-3)/5 үлестірім заңдылығына бағыныштыкездейсоқ шаманың реализациясын табыңыз + x=3
Берілген z = 0,6бойынша Ғ(х) = х-4үлестірімзаңдылығына бағынышты кездейсоқ шаманыңнақтыламасын табыңыз.+ x=4,6.
Биномдық үлестірімнің математикалық үмітін
Биномиалды үлестірімді алған ғалым? +Бернулли
Биномиалды үлестірімді кім алған? +Бернулли
Биномиалды үлестірім р және (1-р) ықтималдықты қандай сұлба бойынша n сынақтардағы колайлы нәтижені сипаттайды? +"сәттілік-сәтсіздік" сұлбасы
Биномиалды
үлестірімде
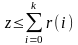 шартының орындалуына қажетті к
итерациялар санына тең?vдискретті
кездейсоқ шамасына те
шартының орындалуына қажетті к
итерациялар санына тең?vдискретті
кездейсоқ шамасына те
Биномиалды
үлестірімде n үлкен және р
кішкентай
мәндерінде келесі теңдік тексеріледі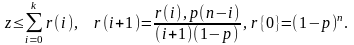
Биномиалды
үлестірімде р
кішкентай
және n
үлкен мәндерінде келесі теңдік
тексеріледі: + 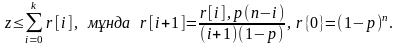
Биномиалды
үлестірімде
n
-тізбекті сынақтардан "сәттіліктер"
к
рет пайда болу ықтималдығы келесі
формуламен өрнектеледі: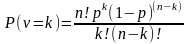 Моделдеудің
кемшілігі неде?+жүйе
параметрлерінің орнықты мәндеріне,
кіріс ақпаратқа және бастапқы шарттарға
тәуелді жеке сипатты болу
Моделдеудің
кемшілігі неде?+жүйе
параметрлерінің орнықты мәндеріне,
кіріс ақпаратқа және бастапқы шарттарға
тәуелді жеке сипатты болу
Биномиалды үлестірімді модельдеу әдісі қандай параметрлердің мәндеріне тәуелді?+nжәне р параметрлерінің
Биномиалды үлестірімділікті модельдеу қандай параметрлердің мәндеріне тәуелді?+nжәне р параметрлерінің
Биномиалды үлестірімнің модельдеу әдісі қандай параметрлердің мәндерімен анықталады?+nжәне р параметрлерінің
Бірқалыпты үлестірім заңдылығы: +P(x=k)= 1/n
Бірқалыпты үлестірім заңдылығына сәйкес формула:+P(x=k)= 1/n
Бірқалыпты
үлестірім заңы дисперсиясы формуласы
қандай? +
Бірқалыпты
үлестірім заңының математикалық үміті
мынаған тең: +
Бірқалыпты
үлестірімді
 кездейсоқ шамасын модельдеу үшін кері
функция әдісімен табылған мына формуланы
қолдануға болады: +
x=a+z(b-a)
кездейсоқ шамасын модельдеу үшін кері
функция әдісімен табылған мына формуланы
қолдануға болады: +
x=a+z(b-a)
Гггггггггггггггггггггггггггг
Гамма
- үлестірімі параметрлерінің мәнін
анықтау үшін мына өрнектерді қолдануға
болады: +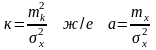
Гамма
үлестірімімен сипатталатын ηкездейсоқ
шамасының нақтыламалары мына формуламен
есептеледі +
Гамма-үлестірімнің дисперсиясын көрсет: +
Гамма-үлестірімнің математикалық үмітін көрсет +
Гамма-үлестірімнің тығыздық функциясы былай өрнектеледі+
Геометриялық үлестірімнің математикалық үміті:+М(v) = тх=(1-р)/р
Геометриялық үлестірімнің диперсиясы неге тең? +D(v)= (1 - р)/р2
Геометриялық үлестірімде жалпы ықтималдық неге тең?+Р(v = k) = (1 – р)k-i р=Рk
Геометриялық
үлестірімді v
кездейсоқ
шамасын модельдеу үшін қандай формуланы
қолдануға болады? + 
Геометриялық үлестірімқандай математикалық үмітпен сипатталады, егер q=(1-p)болса?+ m x = q/p
Геометриялық үлестірімнің математикалық үміті неге тең? +m x = (1-p)/p
Ддддддддддддддддддддд
Дж. Нейманның жалпыланған шығарып тастау әдісі қандай заңдылықтарды модельдеу үшін қолданылады?+Көпөлшемді кездейсоқ шамаларды.
Дж. Фон Нейманның шығарып тастау әдісі қандай кездейсоқ заңдылықтарды модельдеу үшін қолданылады? +Үздіксіз кездейсоқ шамаларды.
Динамикалық модель дегеніміз – +уақыт мезетiне тәуелді жасалатын өзгерiстерге орай объектiлердегi тыныштық пен тепе-теңдiк күйiн бейнелейдi
Динамикалық модельдер дегеніміз – +уақыт мезетiне тәуелді жасалатын өзгерiстерге орай объектiлердегi тыныштық пен тепе-теңдiк күйiн бейнелейдi
Дискретті кездейсоқ шамаларды модельдеудің негізгі әдістері?+ Геометриялық үлестірім, Пуассон үлестірімі,Биномиалды үлестірім
Дискретті
кездейсоқ шамасының үлестіру заңын
қандай үлестірімкестесімен
сипаттайды?+ 
