2 Составление принципиальной схемы
Исходный
код, задающий количество и расположение
ветвей нормального дерева графа:
0 |
3 |
4 |
2 |
Заданный набор компонентов:
D1 |
R1 |
T1 |
L2 |
C1 |
С3 |
S3 |
VT1 |
Q5 |
U2A |
DD2 |
X1 |
ЛА8 |
ИЕ8 |
ЛН3 |
2 |
9 |
1 |
2 |
7 |
2 |
3 |
1 |
1 |
3 |
2 |
1 |
1 |
2 |
3 |
D1 (2) |
R1 (9) |
T1 (1) |
L2 (2) |
C1 (7) |
|
|
|
|
|
С3 (2) |
S3 (3) |
VT1 (1) |
Q5 (1) |
U2A (3) |
|
|
|
|
|
DD2 (2) |
X1 (1) |
ЛА8 |
ИЕ8 |
ЛН3 |
|
|
|
|
|
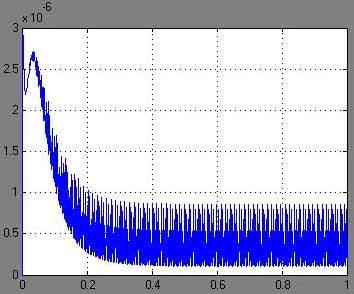
По заданному коду, указывающему количество и место расположения ветвей, восстанавливается нормальное дерево графа. Расставляются хорды к этому дереву в количестве восьми штук. Нумеруются вершины полученного графа, и соотносятся его ветви и хорды с конденсаторами или источниками напряжения и резисторами. Задаются направлениями тока в ветвях и хордах графа.
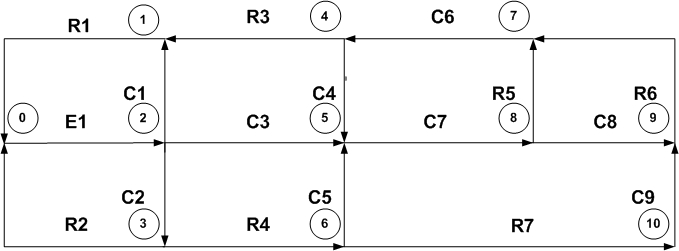
По полученному графу восстанавливается принципиальная электрическая схема.
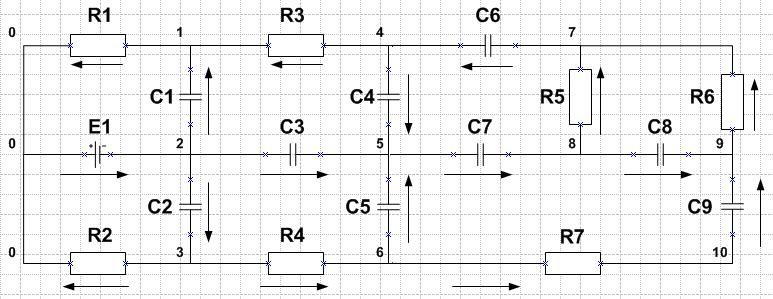
Составляется математическая модель схемы с использованием метода переменных состояния:
Здесь М - матрица контуров и сечений, получаемая на основе построения нормального дерева графа схемы.
Используя М вычисляется вектор резистивных напряжений с помощью топологического уравнения:
.
Получив значения
резистивных напряжений, с учетом
,
можно определить
и вектор резистивных токов в виде системы
уравнений:
По топологическому уравнению:
вычисляется вектор емкостных токов в виде системы уравнений:
Система для вектора
производных переменных состояния, с
использованием компонентного уравнения
Получим
систему уравнений в развернутом виде:
3 Решение сду
Для
решения системы уравнений численными
методами необходимо задаться конкретными
значениями параметров элементов, в
частности величиной сопротивления
резисторов, ёмкостью конденсаторов и
значением напряжения источника. Эти
параметры сведены в таблицу 1.
Таблица 1 ― Исходные значения параметров элементов схемы
Е1, В |
С1, Ф |
С2, Ф |
С3, Ф |
С4, Ф |
С5, Ф |
С6, Ф |
С7, Ф |
С8, Ф |
С9, Ф |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
R7, Ом |
10 |
1∙10-6 |
3∙10-6 |
5∙10-6 |
7∙10-6 |
9∙10-6 |
0,9∙10-6 |
0,7∙10-6 |
0,5∙10-6 |
0,3∙10-6 |
1∙103 |
1,8∙103 |
10∙103 |
6,8∙103 |
33∙103 |
22∙103 |
2∙103 |
В соответствии с выше изложенной технологией решения системы дифференциальных уравнений в среде MATLAB M-файл для ее решения будет выглядеть так:
function dy=vlm(t,y)
dy=zeros(9,1);
dy(1)=-10000-y(1)*(1000+100)+y(3)*100-y(4)*100;
dy(2)=-2000-y(2)*(200+50)+y(3)*50-y(5)*50;
dy(3)=y(1)*20 - y(3)*(20+30)+y(4)*20+y(2)*30+y(5)*30;
dy(4)=-y(1)*14+y(3)*14-y(4)*(14+4+6)-y(6)*(4+6)-y(7)*(4+6)-y(8)*6;
dy(5)=-y(2)*16+y(3)*16-y(5)*(16+55)-y(7)*55-y(8)*55+y(9)*55;
dy(6)=-y(4)*(30+45)-y(6)*(30+45)-y(7)*(30+45)-y(8)*45;
dy(7)=-y(4)*(43+66)-y(6)*(43+66)-y(7)*(43+65+600)-y(8)*(65+600)+y(9)*600;
dy(8)=-y(4)*90-y(6)*90+y(5)*1000-y(7)*(90+1000)-y(8)*(90+1000)+y(9)*1000;
dy(9)=y(5)*1000+y(7)*1000+y(8)*1000-y(9)*1000;
end
После чего в командной строке нужно записать команду на решение диф. Уравнения определенным методом. Например:
[y,t]=ode45('vlm',[0 10],[0 0 0 0 0 0 0 0 0]);
Где [y,t] матрица решений полученных производных от времени t.
Чтобы
получить графические зависимости всех
величин от времени необходимо составить
M-файл,
следующего содержания:
clear;
clc;
[t,y]=ode45(@vlm,[0 1], [0 0 0 0 0 0 0 0 0 ]);
figure; %Расчет напряжений на конденсаторах
subplot(3,3,1);
plot (t, y(:,1)); grid on;
subplot(3,3,2);
plot (t, y(:,2)); grid on;
subplot(3,3,3);
plot (t, y(:,3)); grid on;
subplot(3,3,4);
plot (t, y(:,4)); grid on;
subplot(3,3,5);
plot (t, y(:,5)); grid on;
subplot(3,3,6);
plot (t, y(:,6)); grid on;
subplot(3,3,7);
plot (t, y(:,7)); grid on;
subplot(3,3,8);
plot (t, y(:,8)); grid on;
subplot(3,3,9);
plot (t, y(:,9)); grid on;
figure; % Резистивные токи
Ir1 = (-10-y(:,1))/1000;
subplot(3,3,1);
plot(t,Ir1);
grid on;
Ir2 = (-10-y(:,2))/1800;
subplot(3,3,2);
plot(t,Ir2);
grid on;
Ir3 = (y(:,1)-y(:,3)+y(:,4))/10000;
subplot(3,3,3);
plot(t,Ir3);
grid on;
Ir4 = (-y(:,2)+y(:,3)-y(:,5))/6800;
subplot(3,3,4);
plot(t,Ir4);
grid on;
Ir5 = (-y(:,4)-y(:,6)-y(:,7))/33000;
subplot(3,3,5);
plot(t,Ir5);
grid on;
Ir6 = (-y(:,4)-y(:,6)-y(:,7)-y(:,8))/22000;
subplot(3,3,6);
plot(t,Ir6);
grid on;
Ir7 = (y(:,5)+y(:,7)+y(:,8)-y(:,9))/2000;
subplot(3,3,7);
plot(t,Ir7);
grid on;
figure; %Напряжение на резисторах
Ur1 = (-10-y(:,1));
subplot(3,3,1);
plot(t,Ur1);
grid
on;
Ur2 = (-10-y(:,2));
subplot(3,3,2);
plot(t,Ur2);
grid on;
Ur3 = (y(:,1)-y(:,3)+y(:,4));
subplot(3,3,3);
plot(t,Ur3);
grid on;
Ur4 = (-y(:,2)+y(:,3)-y(:,5));
subplot(3,3,4);
plot(t,Ur4);
grid on;
Ur5 = (-y(:,4)-y(:,6)-y(:,7));
subplot(3,3,5);
plot(t,Ur5);
grid on;
Ur6 = (-y(:,4)-y(:,6)-y(:,7)-y(:,8));
subplot(3,3,6);
plot(t,Ur6);
grid on;
Ur7 = (y(:,5)+y(:,7)+y(:,8)-y(:,9));
subplot(3,3,7);
plot(t,Ur7);
grid on;
figure; %Токи конденсаторов
Ic1 = Ir1+Ir2;
subplot(3,3,1);
plot(t,Ic1);
Ic2 = Ir1-Ir3;
subplot(3,3,2);
plot(t,Ic2);
Ic3 = Ir2+Ir4;
subplot(3,3,3);
plot(t,Ic3);
Ic4 = -Ir3+Ir5+Ir6;
subplot(3,3,4);
plot(t,Ic4);
Ic5 = Ir4-Ir7;
subplot(3,3,5);
plot(t,Ic5);
Ic6 = Ir5+Ir6;
subplot(3,3,6);
plot(t,Ic6);
Ic7 = Ir5+Ir6-Ir7;
subplot(3,3,7);
plot(t,Ic7);
Ic8 = Ir6-Ir7;
subplot(3,3,8);
plot(t,Ic8);
Ic9 = Ir7;
subplot(3,3,9);
plot(t,Ic9);
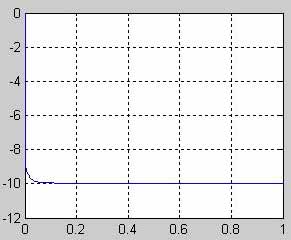
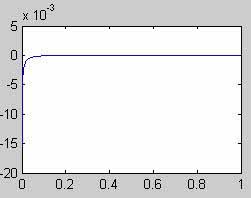
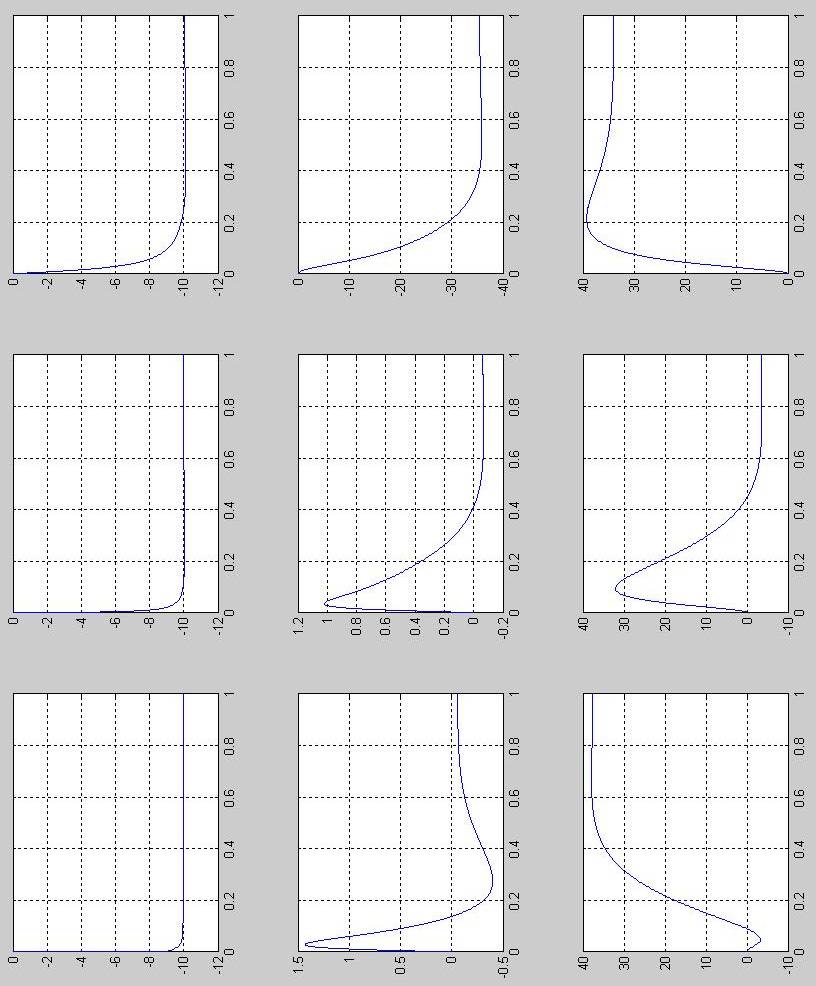Результаты м-файла:
1) Напряжения на конденсаторах
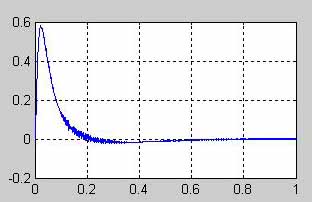
2)
Напряжение на резисторах
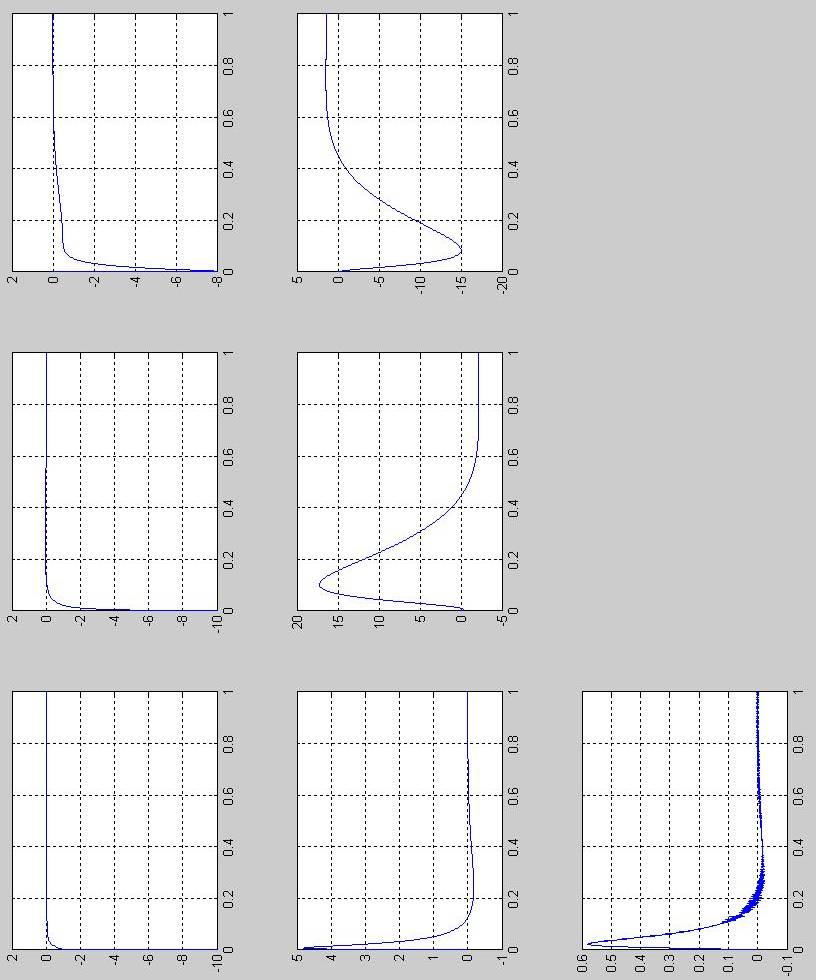
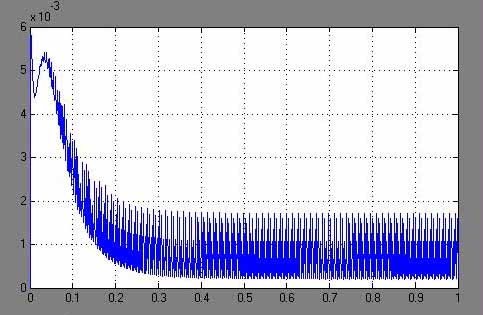
3)
Токи на конденсаторах
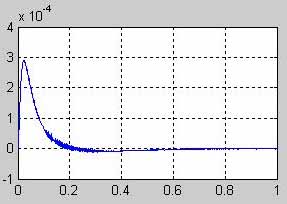
4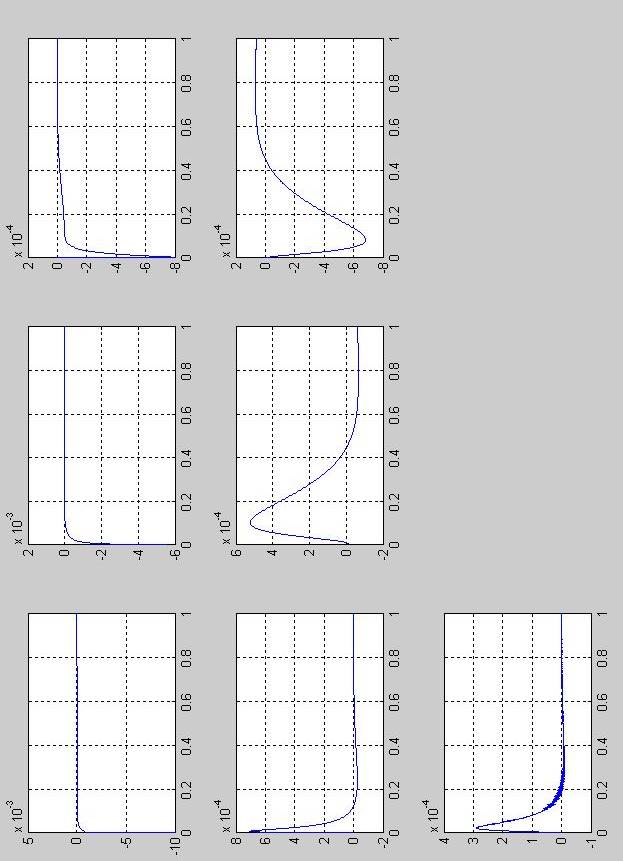
)
Токи на резисторах
4
Моделирование в Simulink
Моделирование
в пакете Simulink
произведем для проверки результатов
полученных путем решения СДУ в ручную.
Для этого соберем схему и подключим
вольтметры и амперметры.
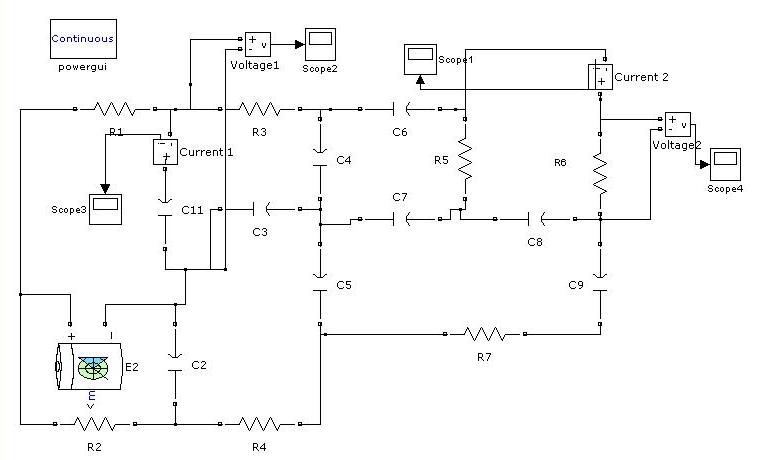
Сравним напряжения и токи полученные путем моделирования с расчетными на конденсаторе С1:
|
Расчетные |
Моделирование |
U,В |
|
|
I,А |
|
|
Из
графиков можно сделать вывод, что
расчетные данные совпадают, но направление
токов не совпадает, т.к. напряжение
полученное путем моделирования имеет
обратную полярность.
Сравним напряжения и токи полученные путем моделирования с расчетными на резисторе R7:
|
Расчетные |
Моделирование |
U,В |
|
|
I,А |
|
|
Из графиков можно сделать вывод, что расчетные данные совпадают.