В. 29 Теорема о выпуклости множества допустимых решений задачи лп.

Теорему доказываем только для задачи канонического вида: c*х → min; A*x=b; x≥0.

Т. Множество допустимых решений задачи ЛП является выпуклым.

Док-во:

A*x=b и x≥0 – ограничения,

x’=(x₁’, x₂’,…, x_n’)

x”=(x₁”, x₂”,…, x_n”)

x’, x” ≥0

Ax’=Ax”=b

Каждое уравнение умножаем на α (α₁, α₂ - произвольные положительные числа, в сумме дающие 1) и складываем их.

α₁Аx’ + α₂Аx”=bα₁ + bα₂

Ax=b

Точка х, лежащая на отрезке xЄ[x’; x”] должна удовлетворять ограничениям задачи. Весь отрезок [x’; x”], состоит из допустимых точек. Из этого следует, что множество допустимых решений является выпуклым, т.к. вместе с другими двумя точками содержит весь отрезок.

В. 30 Теорема о местоположении оптимального решения задач лп.

Т: Если задача ЛП имеет конечное оптимальное решение, то оно находится в крайней точке допустимого множества.

Док-во: Пусть имеется k крайних точек. Если решение находится в одной из них, то теорема доказана.

Предположим, что ни в одной из этих точек решений нет. Решение находятся в точке х⁰, которая находится внутри допустимого множества.

cx⁰<cxⁱ, (i=1,…,k), в точке х⁰ целевая функция min.

Поскольку х⁰ не является крайней, её можно представить в виде выпуклой комбинации крайних точек.

(подставим в уравнение)

Получили противоречие cx⁰>cxⁱ, т.к. предположили, что решение не находится в угловой точке, => решение находится в угловой точке.

В. 31 Теорема о местоположении множества оптимальных решений задачи ЛП.

Т: Если оптимальное решение находится более чем в 1 крайней точке, то оно достигается в любой точке, которая является выпуклой комбинацией этих точек.

Док-во: Пусть x¹,…,x^k - крайние точки, в которых значение целевой функции оптимально.

x¹,…,x^k – крайние точки.

(т.к. ).

В. 32 Теорема о крайней точке.

Т: Для того, чтобы вектор х был базисным допустимым решением, необходимо и достаточно, чтобы он был крайней точкой допустимого множества.

Требуется доказать: х – БДР  х – крайняя точка.

(1) Доказать: Если х – БДР => х – крайняя точка

Пусть х - БДР, тогда без ограничения общности считаем, что первые m координат являются базисными x=(x₁, x₂,…, x_m, 0,0,…0), т.е. единичная матрица стоит в начале. Сделаем предположение, что х - не крайняя точка. Тогда по определению крайней точки можно отыскать 2 вектора x’, x” (x’= x”), что х представляется в виде их линейной выпуклой комбинации, т.е. х=α₁х’+α₂х” (т.е. точка – середина отрезка), где α₁+α₂=1, α₁, α₂ ≥0.

Т.к. все неотрицательны (условие задач ЛП)

Т.к. сумма «+» чисел = 0, они все равны 0.

Т.к. не может быть = нулю, следовательно, . Далее, из этого => x’ и x” - БДР.

Аx’=b

Ax”=b; произведение матрицы на вектор можем переписать 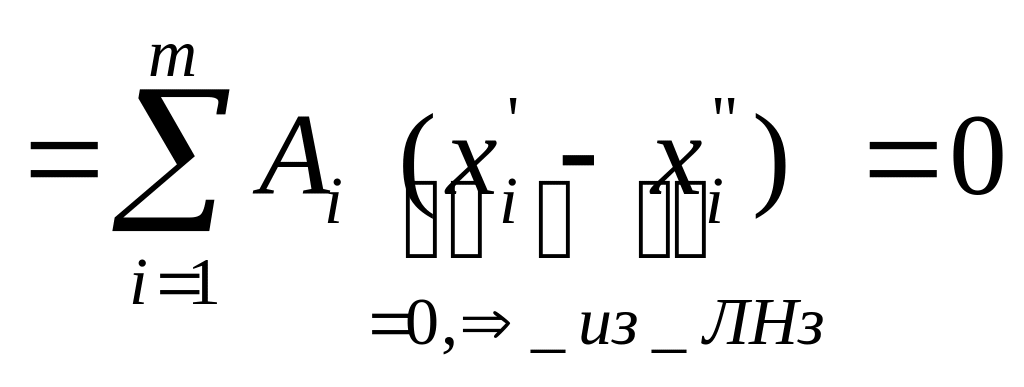(x’-x” - соответствующие координаты)

Первые m столбцов матрицы А - линейно-независимы (по условию), т.е. А₁….A_m – ЛНз, x’=x” i=1,..,m. Получили противоречие, т.к. изначально x’ и x” – разные.

(2) Доказать: Если х – крайняя точка => х – БДР.

Предположим, что х - кр. точка. Если х = 0, то любой набор ЛНз столбцов будет базисным, и такой набор всегда можно найти. Если х=0 => х – БДР.

Пусть x≠0, без ограничения общности получим, то именно первые r координат ≠ 0, т.е. x=(x₁, x₂,…, x_r , 0,0,…0).

Т.к. х находится в допустимом множестве, он удовлетворяет ограничениям задачи. Перепишем как . Если окажется, что вектора - столбцы А₁….A_r – ЛНз, то тогда х – БДР и теорема доказана.

Предположим, что А₁….A_r – ЛЗ, то существует набор констант α₁…α_r не все = 0 одновременно, так что: . Перепишем сумму в матричной форме: .

Построим 2 новых точки: , где t>0.

Рассмотрим: т.о., вектора u, v удовлетворяют системе ограничений осталось убедиться, что u,v≠0 (при этом t – очень маленькое число, неравное 0).

t выбираем настолько маленьким, чтобы комбинации U и V остались положительными (при умножении на t). Это и означает, что U и V являются допустимым решением задач.

, это означает, что х лежит на середине, т.е. он не является крайней точкой. Получили противоречие, т.к. предположили, что вектора А₁….A_r – ЛЗ. След-но, они ЛНз и х – БДР.

Смысл:

1. Симплексный метод перебирает БДР (БДР меняется)

2. По теореме о крайней точке БДР являются угловыми точками

3. В вопросе 30 было доказано, что оптимальное решение обязательно находится в угловой точке.

Теорема о крайней точке показывает, что симплексный метод ищет решение как раз среди угловых точек, т.е. действительно ищет оптимальное решение.

В. 33 Обоснование критерия оптимальности в ПСМ.

Ax = b, в развёрнутом виде:

Мы считаем, что именно первые m переменных – базисные.

Умножим 1 стр. на 1 столбец: . Аналогично: и .

Этим мы выразили базисные переменные через небазисные. Сделаем следующее: возьмём Ц.Ф. и разобьем на 2 части:

( ) .

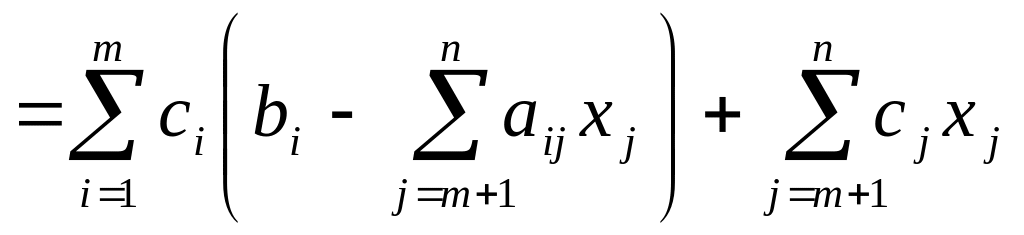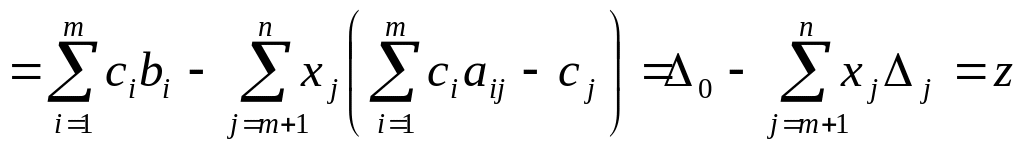Раскрываем скобки: ( ) (вынесем за скобку ) (где - старое значение Ц.Ф.), а остальные переменные = 0).

Мы получили выражение для значения Ц.Ф. через оценки и не базисных переменные.

Значения ц.ф. зависят от оценок не базисных переменных. Если все оценки ≤0 (задача оптимально решена), то какую бы небазисную переменную мы не увеличили, z будет расти, а у нас задача на min и надо, чтобы она убывала.

Если оценка «+», то уменьшается. Если существует хоть одна «+» оценка, то переменная, которой она соответствует, может уменьшить значения ц.ф. Чем > значение оценки, тем больше уменьшится ц.ф. Именно поэтому мы выбираем max «+» оценку, хотя это делать не обязательно. Теоретически, можно брать любую «+» оценку, на практике – max.

Замечания:

Если бы задача была на max, то критерием оптимальности было бы то обстоятельство, что все оценки ≥ 0, а для выбора ведущего столбца нужно искать max по модулю «-» оценку.

В. 34 Обоснование выбора ведущей строки.

При переходе от одного базиса к другому, мы должны внести в базис новую переменную (х_s). При этом, одна из базисных переменных должна стать = 0 и покинуть базис.

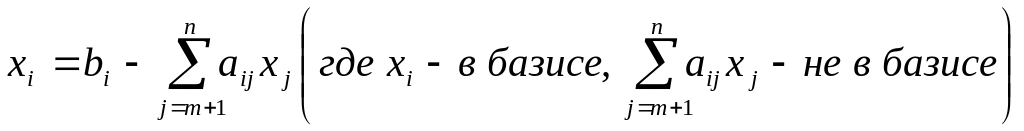
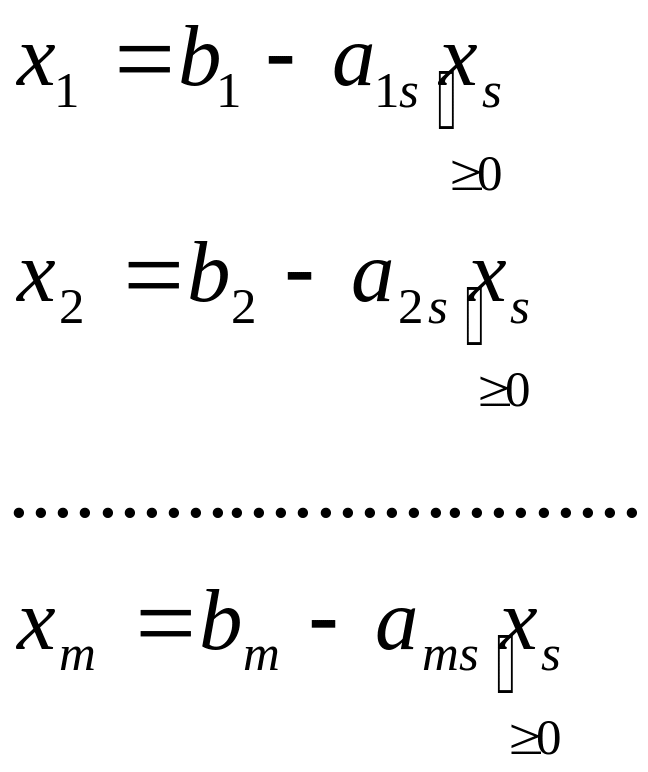
Перепишем комбинацию:

………

, только при условии, что a_is>0).

, т.о.Xs нельзя неограниченно увеличивать

То значение i, на котором достигается min и будет номером переменной, покидающей базис.

В. 35 Обоснование неограниченности Ц.Ф.

Предположим:

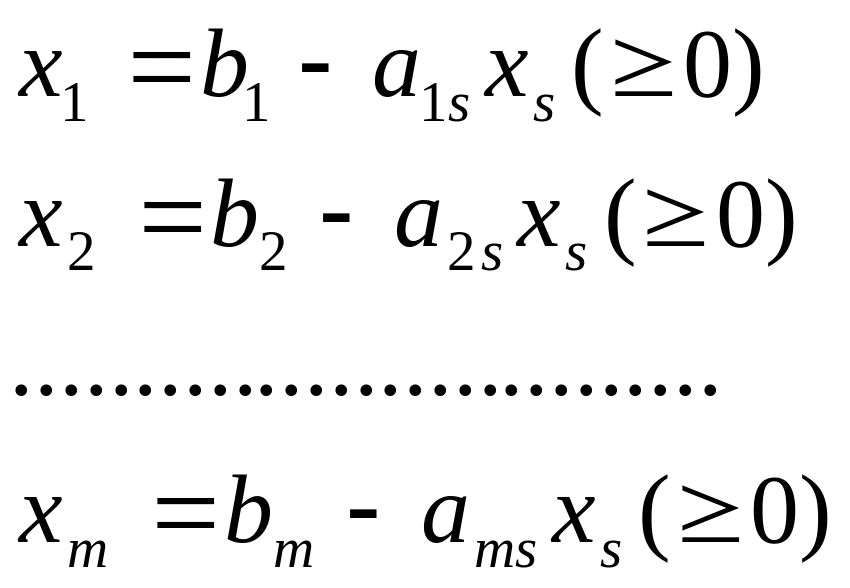
Все (весь ведущий столбец убывающий («-»)).

Неограниченное увеличение Xs влечёт за собой неограниченное увеличение базисных переменных. А это означает неограниченное уменьшение ц.ф. (улучшение). Самого лучшего результата мы не достигнем никогда, т.к. ц.ф. неограниченна.

В. 36 Геометрическая интерпретация симплексного метода.

В общем случае каждому ограничению соответствует полупространство, пересечение всех полупространств образует выпуклый многогранник.

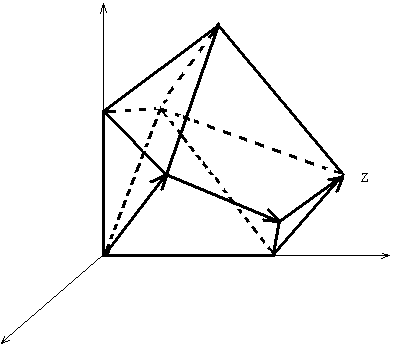
Мы знаем, что решение находится в одной из угловых точек, а угловая точка является базисным допустимым решением. Смысл симплексного метода в том, что, начав с какого-либо базисного допустимого решения, перебирая базис, двигаться от одной угловой точки к другой по направлению к оптимальному решению.

В. 37 Условие не повторяемости базисов.

х¹,х²,….,х^k

cx¹ ≥cx ²≥cx ³ ….≥…≥…..- симплексный метод уменьшает функцию.

Если целевая функция строго уменьшалась, то базисы, которые были до этого момента, никогда больше не повторятся.

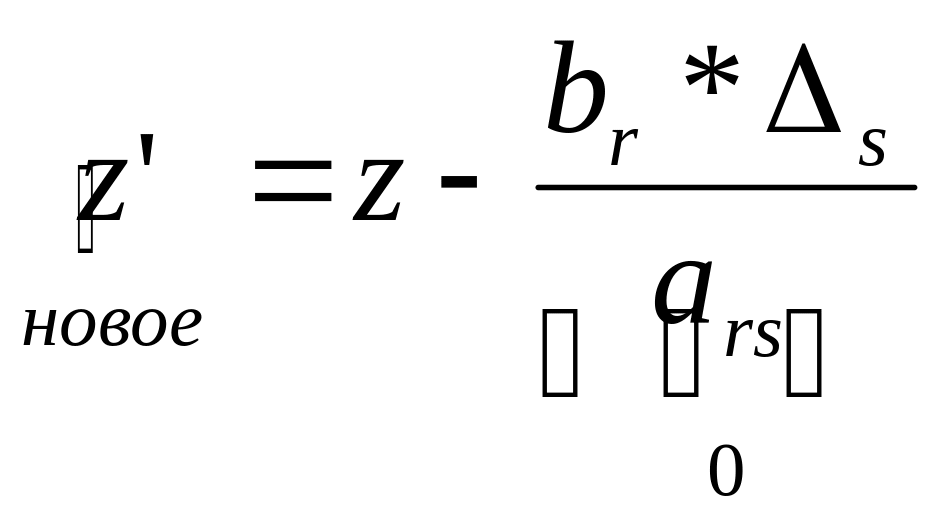, где, ∆s- оценка.

Единственный случай, когда целевая функция не уменьшается, а остается прежней, когда значение БДР в ведущей строке = 0.

Если задача вырожденная (базис вырожденный), то целевая функция может остаться прежней, если задача не вырожденная, то целевая функция всегда будет уменьшаться, и базисы никогда не повторятся.

В. 38 Обоснование конечности симплексного метода и случай зацикливания.

Если задача невырожденная, то базисы никогда повторяться не будут (предыдущий вопрос).

,m- число ограничений.

_{C =} количество всевозможных базисов конечно, метод остановится.

Если задача вырожденная, то может возникнуть зацикливание, то есть возвращение к базису, который уже был.

Существуют методы, позволяющие избежать зацикливания, на практике такое никогда не встречается.

В реальных задачах число итераций симплексного метода равно ~3/2 m (показывает среднее количество итераций), где m- число ограничений.

В. 39 Математическая модель транспортной задачи.

Имеется m - складов и n - магазинов. На складах хранится некоторое количество однородной продукции.

Склад № i имеет запас продукции = a_i ( i= 1,2..m)

Каждый магазин имеет потребность в продукции b_j (j=1,2,..n)

Стоимость перевозки единицы продукта из склада i в магазин j = Сij – за 1 единицу товара.

Задача: Определить объём перевозки из каждого склада в каждый магазин так, чтобы суммарные затраты на перевозки были min.

Пример в тетради!

Потребуем, чтобы .

Построим математическую модель.

1) (х_ij показывает сколько везем, с_ij- сколько стоит)

2) (выводим с i-го склада столько, сколько на нём имеется).

3) (привозим в j-ый магазин столько, сколько ему нужно).

4) х_ij≥0

1-4 - это транспортная задача в матричной подстановке.

Если выполнено условие (*), то транспортная задача всегда имеет решение, например: ( не оптимально).

Если выполняется условие (*), то транспортная задача называется закрытой (замкнутой).

Если исходная задача не замкнута, то имеются 2 возможности:

1) (запасы > потребностей), добавляем фиктивный магазин (свалку).

Потребности магазина: Цены перевозок на свалку = 0.

2) (потребности > запасов), вводим фиктивный склад;

В. 40 Теорема о ранге матрицы ограничений транспортной задачи.

Транспортная задача это частный случай задачи ЛП, поэтому она может быть записана в каноническом виде.

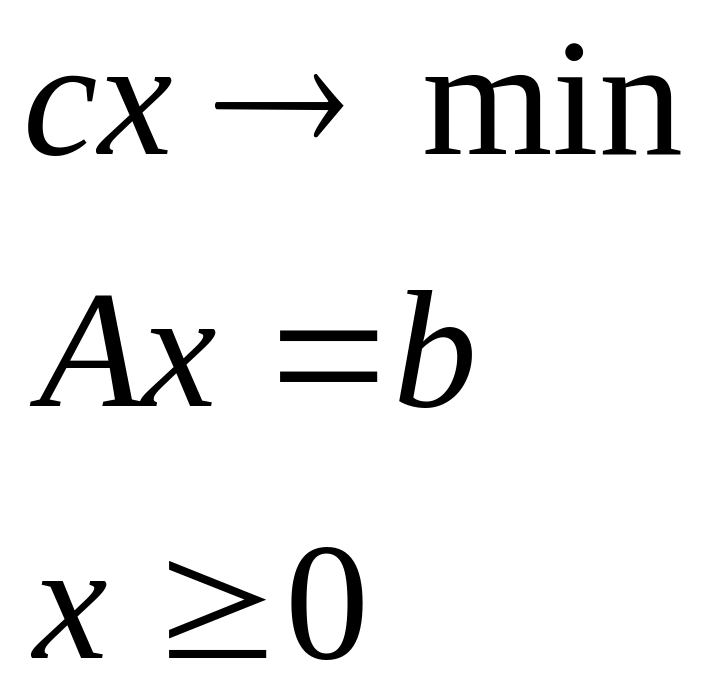
Пример в тетради!

В общем виде, когда у нас m складов и n магазинов, матрица имеет вид:

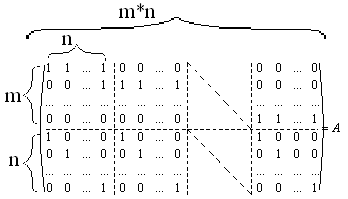
Теорема: rang A= m+n-1

Теорема говорит о том, что в этой матрице m+n-1 - линейно независимых строк.

В этой системе уравнений (A*x=b) остается 1 свободная переменная, т.е. решений может быть несколько.

В. 41 Метод северо-западного угла.

Для того чтобы решить транспортную задачу, надо придумать начальное базисное решение (по методу северо-западного угла)

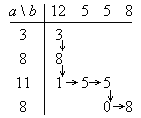
По диагонали ходить нельзя.

Должна появиться m+n-1 базисная переменная.

Поскольку задача является задачей линейного программирования, то можно было бы применить симплексный метод, но для транспортной задачи существует более эффективный алгоритм.

В. 42 Теорема о потенциалах.

Построим к транспортной задаче двойственную.

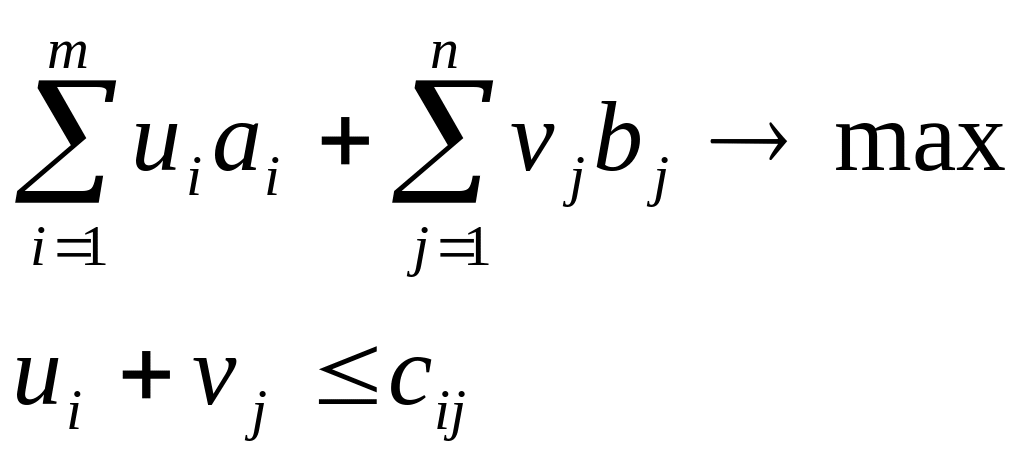
u_i или v_j - двойственные переменные, которые принято называть потенциалами.

Т: Если для базисных клеток выполняется условие: , а для небазисных

, то план перевозок транспортной задачи оптимален.

Доказательства не нужно.

Общий смысл метода потенциалов заключается в том, чтобы решить эту двойственную задачу.

Метод потенциалов выбирает те неравенства, которые не выполняются , и заменяет их на правильные.

В. 43 Алгоритм метода потенциалов.

Метод потенциалов предназначен для решения транспортной задачи в матричной по­становке. Потенциалы - это двойственные переменные. Сам метод - прямой, на каждом шаге выбирается одно из двойственных ограничений, которое не выполняется и исправ­ляется таким образом, чтобы не нарушить ограничения прямой задачи. Постепенно в двойственной задаче ограничения будут выполнены, что будет означать оптимальность в прямой задаче.

Таблица для метода потенциалов имеет следующий вид:

	b1…	bj	...bn	u
a1 …				u1 …
ai		cij		ui
		xij
… am				… um
v	v1	vj	…vn	z

Каждая ячейка (i, j) таблицы хранит информацию о цене (с_ij) и о количестве перевозимого товара (x_ij). В процессе решения задачи часть клеток будем называть базисными (их всегда будет m+n-1), а остальные - небазисными (или свободными).

Алгоритм

Шаг 0. Замкнуть задачу, если она не замкнута. Перейти на шаг 1.

Шаг 1. Нарисовать начальную таблицу. Перейти на шаг 2.

Шаг 2. Рассчитать начальный план перевозок (например, методом северо-западного угла) и выделить базисные клетки. Вычислить значение целевой функции. Перейти на шаг 3.

Шаг 3. Рассчитать значения потенциалов. Положить u₁=0 (или любому другому чис­лу). Остальные потенциалы рассчитать с помощью базисных клеток, исходя из уравнения u_i+v_j=c_ij. Перейти на шаг 4.

Шаг 4. Для свободных клеток рассчитать оценки s_ij=c_ij-v_i-v_j. Если все s_ij≥0, то найдено оптимальное решение. Перейти на шаг 6. Иначе выполнить шаг 5.

Шаг 5. Из небазисных клеток выбрать ту, у которой оценка s_ij минимальна и для нее выполнить следующую процедуру:

• Построить цикл для этой клетки. Цикл - это замкнутая ломаная линия, кото­рая чередует вертикальное и горизонтальное направления и проходит только по базисным клеткам. В исходной клетке поставить «+» и далее по циклу расставить, чередуя, «+» и «-».

• Вычислить λ=min{x_ij : «-»}. Клетку, на которой достигается этот минимум, убрать из базиса (только одну), а клетку (i,j) (у которой минимальная оцен­ка s_ij) сделать базисной.

• Нарисовать новую таблицу, с пересчитанным планом перевозок: для клеток с «+» прибавить λ к х_ij а для клеток с «- » - вычесть. Остальные клетки остаются как были. Пересчитать целевую функцию: z’=z+mins_ij*λ.

Перейти на шаг 3.

Шаг 6 Конец алгоритма.

На шаге 3 у нас m+n-1 уравнений и n+m неизвестных. Поэтому возникает неоднозначность, разрешить которую можно, определив одну из переменных заранее (например, u₁=0).