В. 16 Математическая модель искусственной задачи.

Метод искусственного базиса применяется, если не удаётся отыскать начальный базис. Вместо исходной задачи решается искусственная задача, которая составлена из исходной по определённым правилам, и оптимальное решение искусственной задачи даёт БДР исходной задачи, если последняя имеет решение.

, i=1,…,m

x_j ≥0

В матричной форме:

Искусственная задача строится так:

, i=1,…,m

x_j ≥0, y_i ≥0

y_i -искусственная переменная

В матричной форме: 1*y min; Ax+Ey=b; x≥Θ, y≥Θ, где 1 – единичная матрица.

Пример в тетради!

Если решить искусственную задачу, то единичная матрица переместится в исходные переменные, затем запускаем симплексный метод.

В. 17 Теорема. Обоснование метода искусственного базиса.

Пусть Z*- оптимальное значение целевой функции искусственной задачи.

Теорема: Если Z*=0, то оптимальное БДР искусственной задачи является допустимым БДР исходной задачи. Если Z*>0, то исходная задача не имеет решения.

Док-во: Z*- оптимальное

1) Z*=0 => y_i =0 (все)

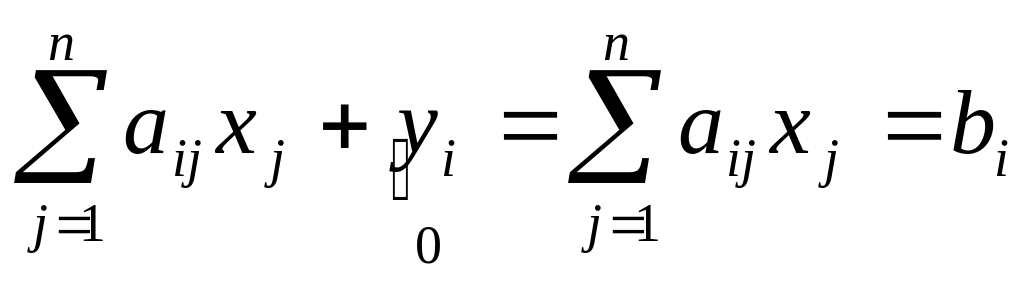- ограничение искусственной задачи

Полученные в ходе решения искусственной задачи значения x удовлетворяют исходной задаче => исходная задача имеет допустимое решение.

2) Z*>0. Предположим, что исходная задача всё-таки имеет решение, которое удовлетворяет ограничению . Но это означает, что если все y_i =0, то решение искусственной задачи тоже удовлетворяет этому же ограничению, и оптимальное значение Z должно было быть=0, а мы предположили, что оно положительно (по условию), следовательно, получили противоречие. Противоречие получили, потому что мы предположили, что решение исходной задачи есть =>, его нет.

В.18 Алгоритм метода искусственного базиса.

Замечание: В методе искусственного базиса прямой симплексный метод применяется дважды. 1й раз – для того, чтобы найти допустимое решение, 2й – для того, чтобы найти оптимальное решение.

Метод искусственного базиса применяется для решения линейной задачи оптимиза­ции в случае, когда не удается отыскать начальное БДР. То есть матрица ограничений не содержит единичной подматрицы.

Алгоритм метода искусственного базиса

Шаг 0. Построить начальную симплексную таблицу:

	Базис	БДР	x1	x2	…	xn	y1	y2	…	ym
1	y	b	А				Е
	z	∆0	∆1	∆2	…	∆n	∆n+1	∆n+2	…	∆n+m

Оценки ∆_n+1,…, ∆_n+m будут равны нулю. Остальные оценки вычисляются по формуле:

∆₀ = 1*b, ∆_j = l*A_j, где 1 – это вектор из m единиц.

Искусственные переменные y₁,…,у_т образуют базис.

Шаг 1. К таблице применить ПСМ. Проверить значение целевой функции z, если оно больше нуля, то исходная задача решения не имеет. Перейти на шаг 3. Если z=0, то возможны два случая:

• В столбце «Базис» только исходные переменные х_j. Перейти на шаг 2.

• В столбце «Базис» имеются искусственные переменные. Такие переменные заменяются на исходные с помощью преобразования Жордана-Гаусса. Для этого выбирается ведущая строка с искусственной переменной, и ведущий столбец - любой столбец, не находящийся в базисе, но такой, чтобы ведущий элемент не был равным нулю. После избавления от искусственных перемен­ных перейти на шаг 2.

Шаг 2. Отбросить столбцы, соответствующие искусственным переменным, стереть оценки и вычислить новые в соответствии с исходной целевой функцией. Применить к получившейся таблице ПСМ. Перейти на шаг 3.

Шаг 3.

Пример в распечатке!

В. 19 Замечание к методу искусственного базиса.

Замечание 1. В начальной симплексной таблице оценки при переменной х_j = сумме элементов j-го столбца, а оценки при переменных y будут = 0.

Замечание 2. Если k<m столбцов уже образуют часть единичной матрицы, то достаточно ввести только m-k искусственных переменных.

Пример: x₁+2x₂→min

2x₁+1x₂=5

3x₁+0x₂=6

x₁,x₂≥0

y₁ →min (вводится только 1 переменная)

2x₁+x₂+0=5

3x₁+0x₂+ y₁=6

x₁, x₂,y₁≥0

Замечание 3. Если в исходной задаче все ограничения были типа ≤, то дополнительные переменные уже образуют базис, поэтому метод искусственного базиса применять не нужно.

В. 20 Двойственность ЛП.

Рассмотрим задачу об оптимальном распределении ресурсов.

Предположим, что у нас сейчас: 2 вида продукта (n=2), 2 вида ресурса (m=2); c₁, c₂ – цены товаров; b₁, b₂ - объём ресурсов; x₁, x₂ – количество товаров; a_ij – норма расхода i-го вида ресурса, необходимого для получения j-го вида продукции.

P: с₁x₁+с₂x₂→max

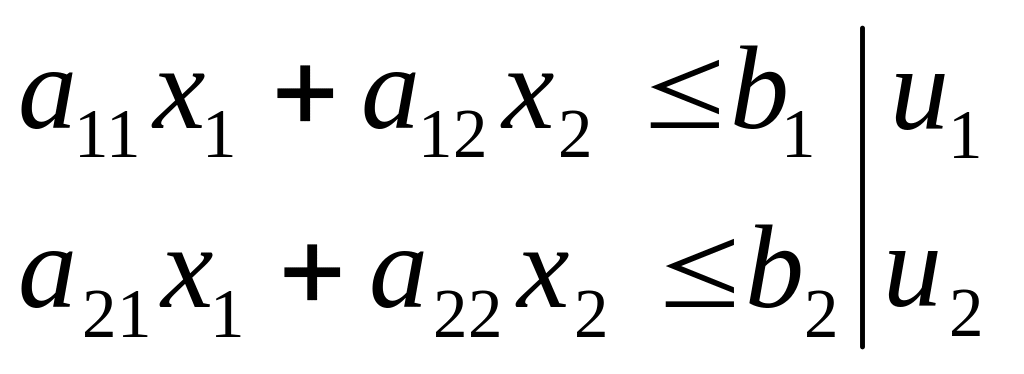
x₁, x₂≥0

Предположим, что предприятие может продавать эти ресурсы. Продавать нужно по таким ценам, чтобы с одной стороны, это было не слишком дорого, с другой - прибыль должна быть не<, чем, если бы мы эти ресурсы переработали. Цены ресурсов (u₁ и u₂) по которым будем продавать.

D: b₁u₁+b₂u₂→min – деньги, которые получим от продажи.

a₁₁u₁+a₂₁u₂≥c₁ – по чём мы продадим единицу товара х₁.

a₁₂u₁+a₂₂u₂≥c₂

u₁, u₂≥0

Задача D называется двойственной к задаче P. Переменные u_i называются двойственными оценками (или теневыми ценами, или справедливыми).

Если больше 2-х переменных.

P:

, i=1…m

x_j ≥0, j=1…n

D:

, j=1…n

u_i ≥0, i=1…m.

В. 21 Соответствие между прямой и двойственной задачей.

	P	D
Целевая функция	min	max
Переменные	xj	ui
Правая часть ограничения	bi	cj
Матрица ограничений	A	AT
Коэффициенты целевой функции	cj	bi
Соответствие знаков огранич. и перемен. при → min	≥	ui ≥0
	≤	ui ≤0
	=	ui - ЛЗ
	xj ≥0	≤
	xj ≤0	≥
	xj - ЛЗ	=

ЛЗ – любого знака

Пример в тетради!