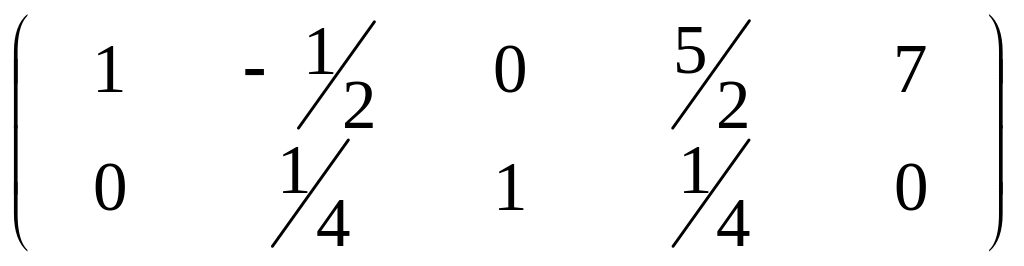В. 1 Определение мат. Программирования и факторы, способствовавшие его возникновению.

Мат.програм – раздел математики, который изучает теории и методы решения конечномерных задач оптимизации.

Задача оптимизации – задача, в которой нужно отыскать наибольшее или наименьшее значение вещественной функции в заданной области. Область, как правило, задается системой равенств и неравенств.

Область – ограничения (например время).

Вещ.функция – это цель. Под словом «программирование» следует понимать разработку оптимального плана или программы действий.

Примерно в 40-х годах XX века начали появляться эк. задачи, которые нельзя было решить классическим методом. Вместе с этим началось бурное развитие вычислительной техники. Основной метод решения задач оптимизации – симплексный метод – был предложен в 1947 году Джорджем Данцигом.

В. 2 Задача мат. программирования.

X=(x₁, x₂,…,x_n) - вектор переменных (неизвестных)

- функционал

- функционалы, которые нужно максимизировать или минимизировать (целевые функции).

Задача МП состоит в следующем:

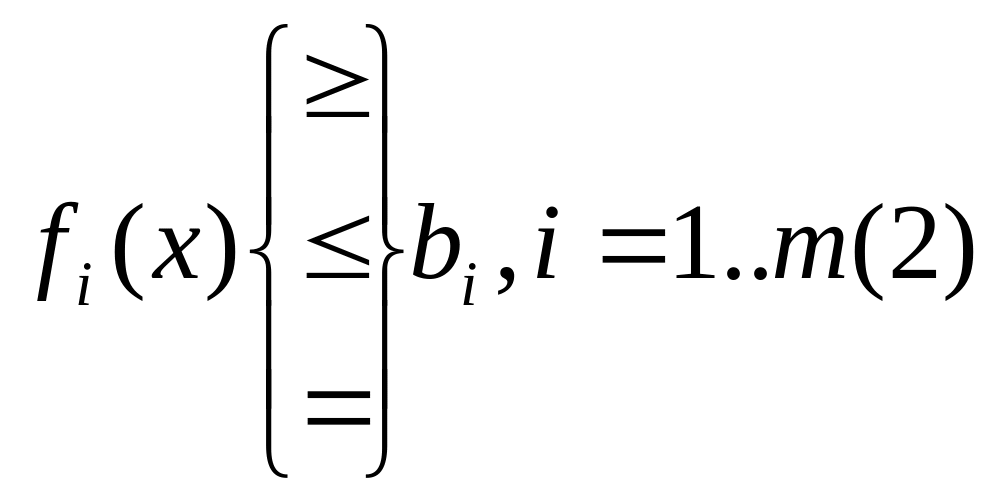
f_i -некоторая вещественная функция

b_i -константы

Выражение (1) определяет набор целевой функции, выражение (2) определяет систему ограничений.

Решения задач (1) и (2) может быть допустимым и недопустимым, а также оптимальным и неоптимальным.

В. 3 Определение допустимого и оптимального решения задачи МП.

Вектор Х называется допустимым решением, если он не противоречит системе ограничений .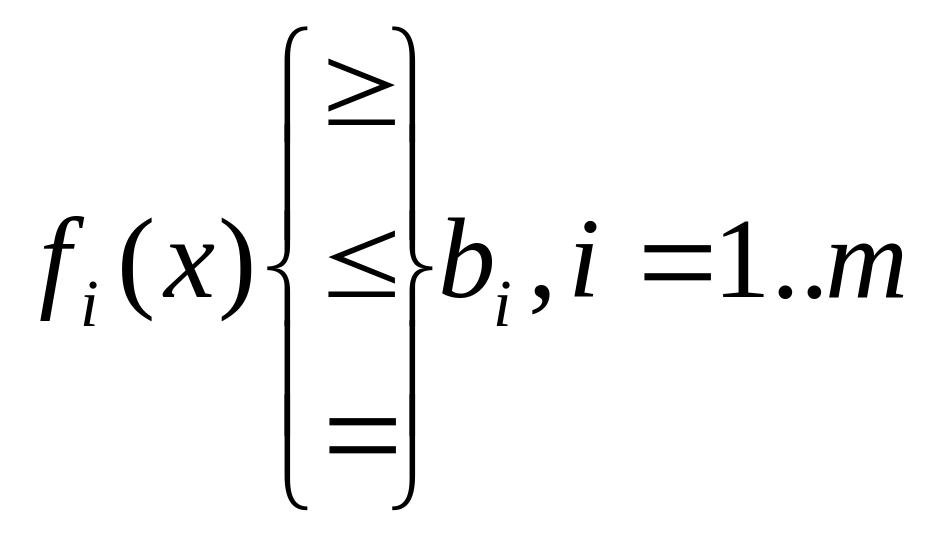

Если хотя бы одно ограничение не выполняется, то вектор Х называется недопустимым решением. Мы будем иметь дело только с задачами, где k=1, т.е. имеет место лишь одна целевая функция g(x).

Допустимое решение x^* называется оптимальным решением, если для любого допустимого Х выполняется неравенство: g(x^*)≥g(x), если задача на максимум или g(x^*)≤g(x) если задача на минимум.

В. 4 Общий вид задачи линейного программирования.

Пусть С=(с₁,с₂,…,с_n) – коэффициент целевой функции, С – вектор цен

X=(x₁,x₂, …,x_n) - вектор переменных

b=(b₁, b₂, …, b_m) - столбец ограничений

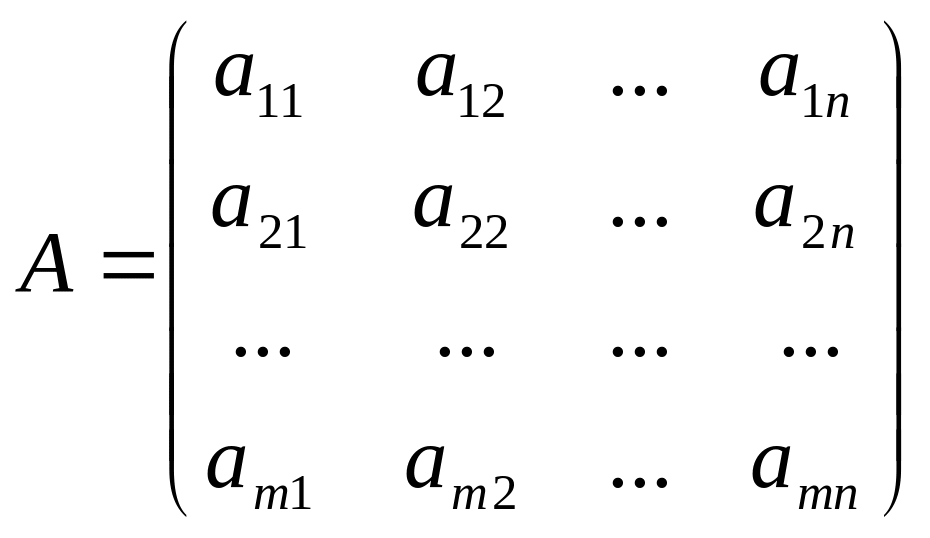- матрица ограничений

Задача линейного программирования записывается в след. виде:

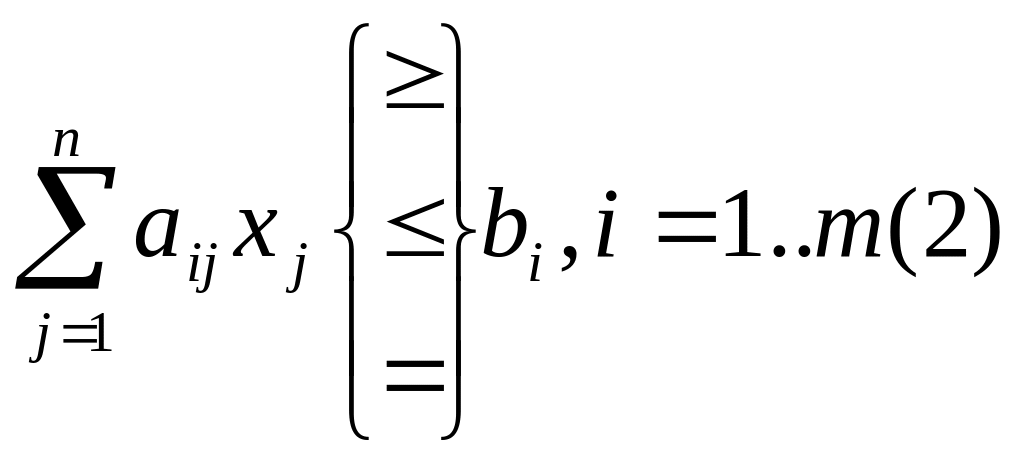
(1)-целевая функция; (2), (3) – ее ограничения.

Матричный вид задачи:

.

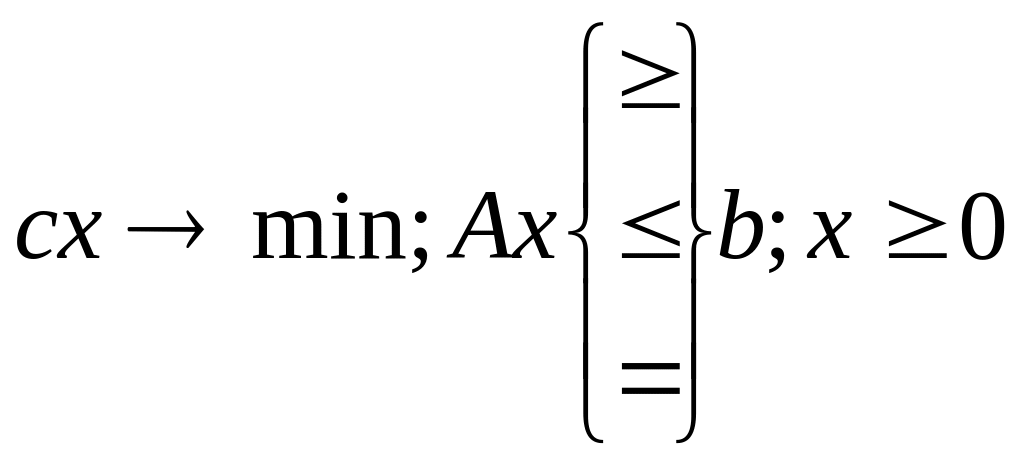Пример в тетради!

В. 5 Канонический вид задачи ЛП

это когда все ограничения имеют тип равенства, а сама задача на минимум. , или

Любую задачу линейного программирования можно привести к каноническому виду. А любую задачу в каноническом виде можно решить симплексным методом.

В. 6 Преобразование Жордана-Гаусса.

Это преобразование лежит в основе симплексного метода. Пусть есть матрица A_m*n, m<n, m – строки, n – столбцы.

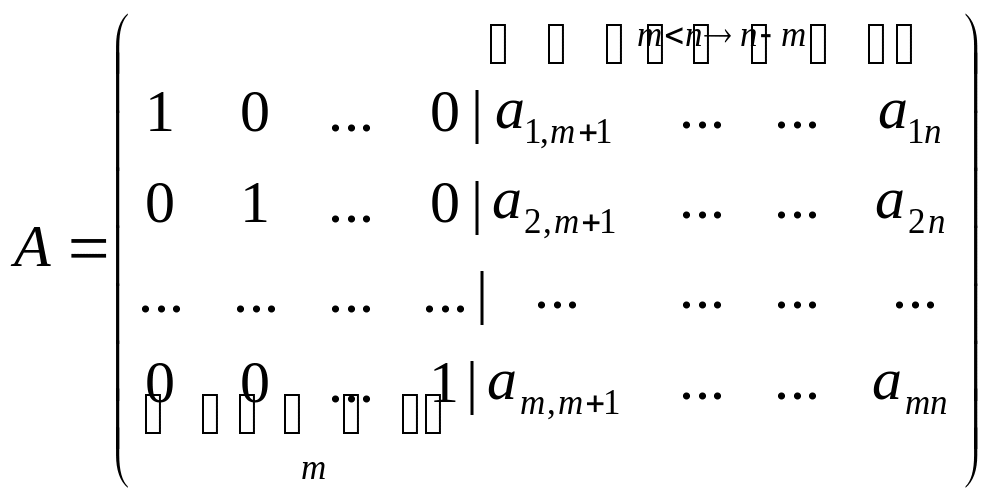
Единичная матрица стоит не обязательно в самом начале, ее столбцы могут быть разбросаны как угодно. Эта единичная матрица образует базис.

Пусть r-ведущая строка (в которой стоит 1), s-ведущий столбец (который хотим сделать единичным). На их пересечении стоит ведущий элемент a_rs.

Преобразование Жордана-Гаусса заключается в том, чтобы путем элементарных преобразований матрицы сделать s-тый столбец единичным, в котором 1 будет стоять в строчке r.

Элементарные преобразования: сложение строк и умножение строки на число.

Преобразование Жордана-Гаусса можно записать в виде двух форм.

- преобразование ведущей строки. a_rj’ - новое значение (деление!).

правило для всех остальных строчек, которые не являются ведущими! (правило креста)

4-ведущий элемент, поделим на него ведущую строку.

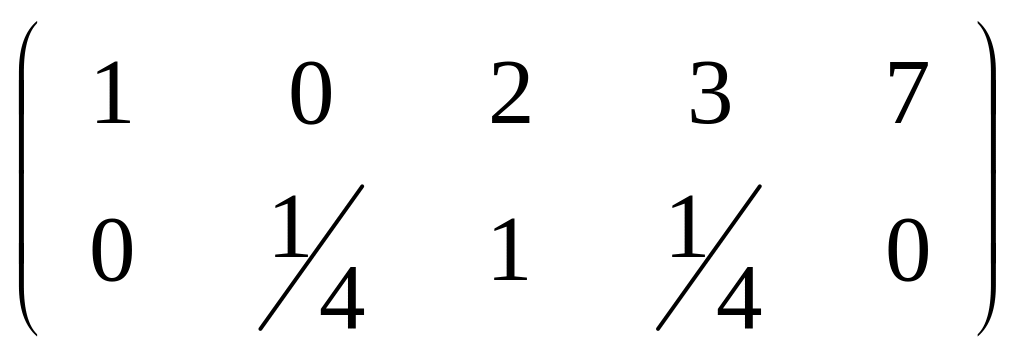нижнюю умножаем на 2 и вычитаем из верхней.