6.4 Общая задача распознавания кривых, метод признаков

Выше рассматривались отклонения в протекании кривой и выяснялся их характер. Метод признаков предназначен для решения более общей задачи распознавания – установления связи между поведением кривой и состоянием системы [6.1].

Пусть имеется некоторое число состояний системы , и предполагается, что каждому состоянию соответствует определенный класс кривых . Предъявляется для распознавания кривая за период времени Т и требуется отнести ее к одному из указанных классов. Для того чтобы свести эту задачу к рассмотренной ранее проблеме распознавания, необходимо охарактеризовать все рассматриваемые кривые в единой системе признаков, т. е. отобразить кривые в конечномерном пространстве признаков. Формирование пространства признаков представляет собой наиболее специфическую часть проблемы распознавания кривых.

6.4.1 Формирование признаков с помощью разложения в ряд по ортогональным функциям.

В качестве признаков кривой на участке t₀ ≤ t ≥ t₁ можно принять коэффициенты разложения функции в ряд Фурье. Не ограничивая общности, будем считать t₀=0 и t₁=T, где T – продолжительность участка наблюдения. На данном участке функция:

(6.33)

где: коэффициенты Фурье:

(6.34)

(6.35)

В соответствии с равенством (6.34) функция на участке длительностью T представлена в виде разложения в ряд по ортогональным функциям:

(6.36)

Система функций {_i, (t)} называется ортогональной на участке (0, Т) если:

(6.37)

Функция представлена в виде суммы элементарных периодических кривых (тригонометрических функций). Обычно некоторое число первых членов разложения дает удовлетворительное представление о поведении функции . Ограничиваясь наибольшей гармоникой (например k≤10), можно охарактеризовать кривую помощью n признаков.

n=2 k+1,

причем признаками становятся величины a₀, a₁, b₁, …, a_k, b_k.

Разложение в ряд по тригонометрическим функциям (ряд Фурье) является наиболее употребительным. Применяется также разложение по полиномам Эрмита, Лежандра, Чебышева и др. Особый интерес для решения диагностических задач представляет разложение в ряд по ортогональным кусочно-линейным функциям [6.1].

Одним из примеров, использования разложения в ряд по ортогональным функциям для диагностики состояния электроэнергетического оборудования, является метод низковольтных импульсов (НВИ), который используется для диагностики механического состояния обмоток силовых трансформаторов [6.10 – 6.12].

Метод НВИ заключается в том, что на одну из обмоток расшинованного трансформатора подается короткий прямоугольный зондирующий импульс низкого напряжения 100-600 вольт, длительностью около 1 мкс и одновременно наблюдается ток на измерительных шунтах, подключенных к другим обмоткам. Таким образом, исследуется переходной процесс, возникающий в обмотках как реакция на воздействие прямоугольного импульса. Предварительно производится паспортизация реакции исправного (или нового) трансформатора на НВИ. Сравнение осциллограмм, записанных до КЗ (нормограмм) и после КЗ (дефектограмм), позволяют оценить состояние трансформатора.

Для интерпретации результатов НВИ использовался [6.10] численный спектральный анализ на основе дискретного преобразования Фурье. Спектральная функция сигнала имеет вид:

(6.38)

где: f – частота; F(t) – функция изменения сигнала в осциллограмме НВИ.

Амплитудный спектр обмотки, т.е. зависимость амплитуды сигнала от частоты f представлена [6.10] в виде:

(6.39)

Для вычислений авторы использовали дискретное преобразование Фурье:

(6.40)

где: n=0, 1, …, 2N-1; N – число интервалов разбиения; t_k – временная координата точки на осциллограмме:

, (6.41)

где: T – длина заданного интервала времени (шаг разбиения), принимаемого при рассмотрении, если выполняется равенство f=n/T.

Переходя от показательной к комплексной форме для реальной и мнимой частей формулы (6.39), авторы получили:

(6.42)

(6.43)

Амплитудно-частотные характеристики обмотки получаются [6.10] путем подстановки (6.42) и (6.43) в (6.39).

На рисунке 6.6 приведены осциллограммы НВИ, при испытаниях фазы А трансформатора ТДЦ-250000/220, после опыта КЗ с 85% нормируемого значения ударного (апериодического) тока [6.10]. После достижения 85% значения тока, в осциллограммах НВИ произошли значительные амплитудно-частотные изменения соответствующие радиальным деформациям в обмотке НН фазы А (рисунок 6.7). Был сделан вывод о невозможности проведения дальнейших испытаний.

Рисунок 6.7 – Фотография обмотки НН трансформатора типа ТДЦ-250000/220, фазы “А” иллюстрирующая потерю радиальной устойчивости обмотки.

Построенные на основе осциллограмм АЧХ (рисунок 6.8), показали, что изменения в спектрах обмоток, вызванные радиальными деформациями, носят в основном амплитудный характер, изменения по частоте менее значительны. Одной из основных резонансных частот рис. 6.6 и 6.8 является частота, соответствующая периоду 3 микросекунды, т.е. 330 кГц. Это подтверждается расчетами спектров – одной из основных резонансных частот является частота 320 кГц.

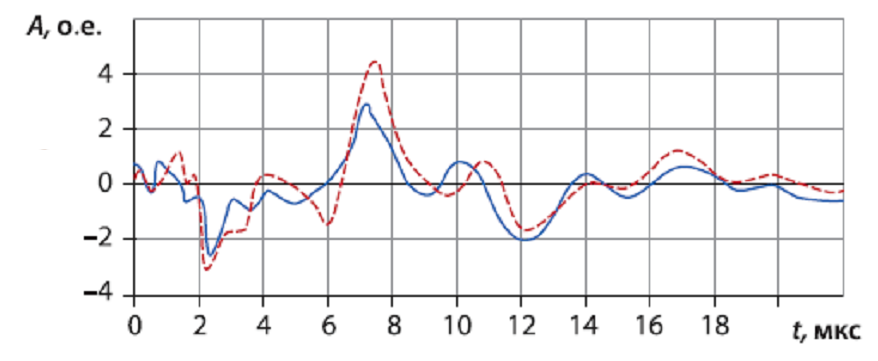
а

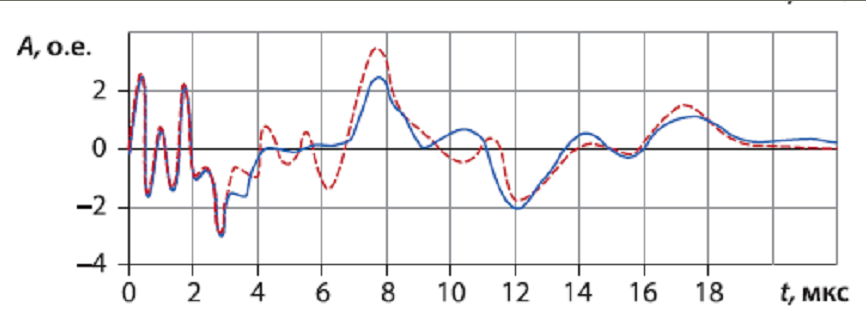
б

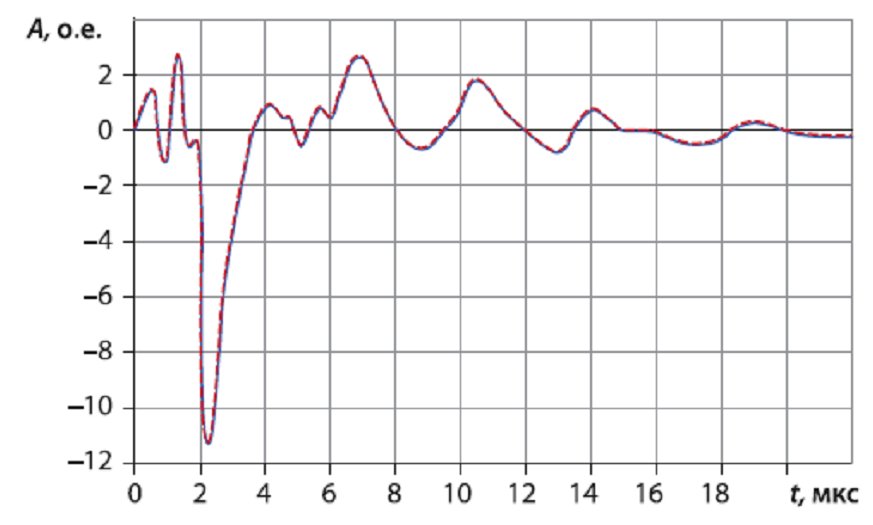
в

а – фазы А-В; б – фазы А-С; в – фазы В-С;

– нормограммы; – переходные процессы в поврежденных обмотках

Рисунок 6.6 – Осциллограммы при НВИ обмотки НН трансформатора типа ТДЦ- 250000/220 после 85% опыта КЗ на фазе А.

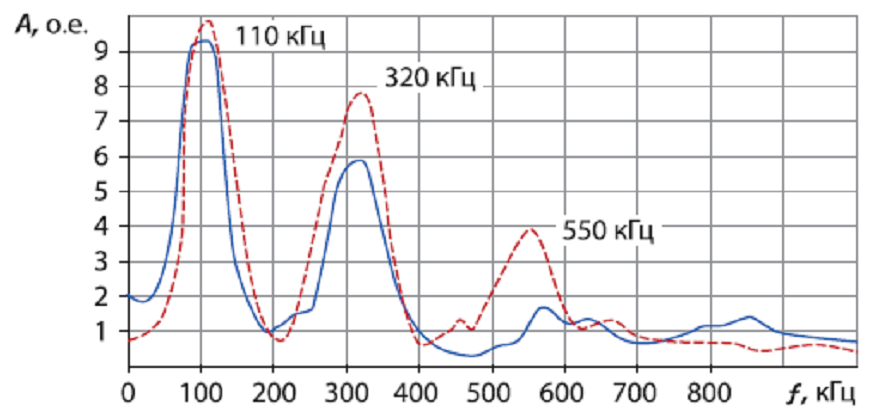
а

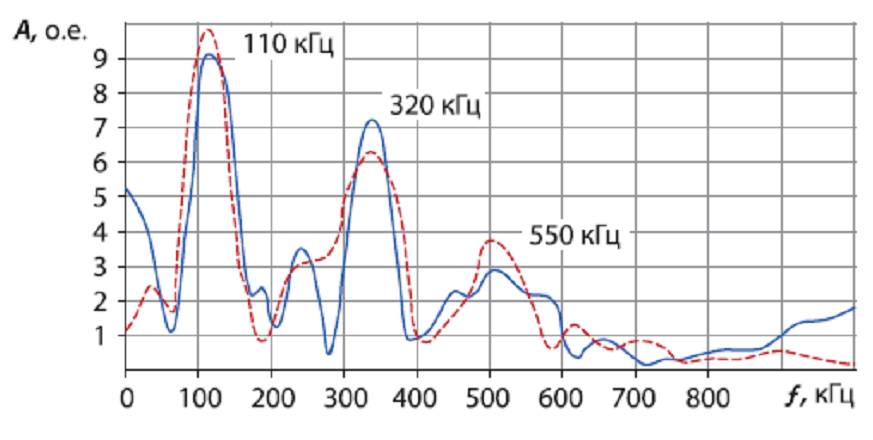
б

а – фазы А-В; б – фазы А-С;

– до 85% -го опыта КЗ на фазе А; – после опыта;

Рисунок 6.8 – АЧХ обмотки НН трансформатора типа ТДЦ- 250000/220.

Математическая обработка результатов НВИ [6.10], на основе спектрального анализа для трансформатора 250 МВА, показала, что для крупных трансформаторов в спектрах их обмоток имеются три резонансные частоты (110, 320 и 500-550 кГц). При возникновении радиальных деформаций амплитуда второй и третьей резонансных частот изменяется в 1,3-2 раза, что наглядно видно из рис. 5.8.

Таким образом, использование метода НВИ позволяет выявлять деформации обмоток высоковольтных силовых трансформаторов на ранней стадии.