6.2 Обнаружение неслучайных отклонений на основе дисперсионного анализа линейной регрессии

Общая математическая модель состояния объекта контроля может быть представлена в виде многомерного вектора показателей (характеристик) [6.3]:

, (6.7)

где: – постоянная составляющая, характеризующая в объекте необратимые изменения; – обратимые изменения; – погрешность измерительных средств контроля.

Считается, что регулярная составляющая представляет собой гладкую функцию от аргумента времени t, описываемую конечным вектором параметров .

Используя терминологию статистического анализа временных рядов 6.3, регулярную составляющую назовем трендом. Случайная составляющая – это случайный процесс с нулевым математическим ожиданием и с достаточно узкой автокорреляционной функцией. Составляющие и (t) определяют стохастическую часть процесса. Для простоты анализа составляющие и (t) можно объединить в процесс (6.7) и записать в виде:

. (6.8)

Процессом постепенного изменения технического состояния объекта контроля будем считать процесс, для которого выполняется соотношение

, (6.9)

где: . – норма вектора.

Действительно, чем сильнее неравенство (6.9), тем ближе процесс к детерминированному, функционально зависящему от времени эксплуатации t. При этом случайный процесс предполагается стационарным по среднему значению, т.е.

. (6.10)

Если выполняется условие (6.10) для процесса (6.8), то он может считаться детерминированным и его можно использовать для прогнозирования технического состояния объекта (например, для оценки остаточного ресурса или параметрического отказа). В таком случае многомерный процесс необратимого изменения технического состояния объекта контроля определяется вектором W(x), t функции времени, постоянных коэффициентов :

, (6.11)

где: – вектор случайных ошибок, не зависящих от длительности эксплуатации.

При больших значениях дисперсий случайных ошибок можно использовать операции сглаживания [6.3], практически сводящиеся к минимизации суммы квадратов отклонений (метод наименьших квадратов):

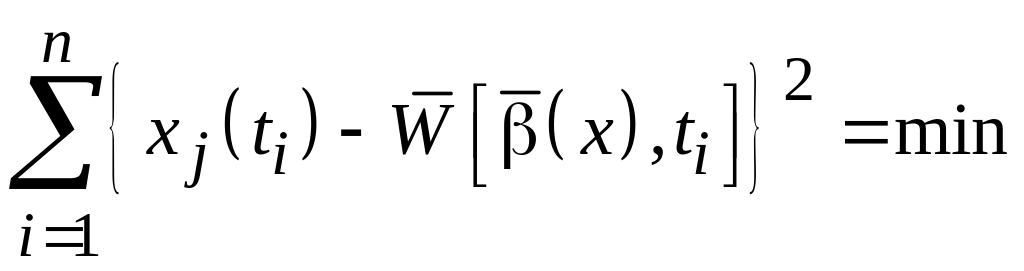, (6.12)

где: x(t_i) – одномерный временной ряд для j-й составляющей вектора Х(t).

Выражение (6.11) позволяет рассматривать измеренные в ходе периодических испытаний значения показателей Х_i как реализации нестационарных по среднему и непрерывных случайных процессов с дискретным временем (временем профилактических испытаний). Под значимостью контролируемого показателя качества будем понимать его способность ощутимо изменять регулярную составляющую W(x), t на фоне случайной величины ε_i, что предполагает превышение изменения тренда f(, t) над средним квадратическим отклонением процесса ² в интервале времени эксплуатации оборудования.

Определение вида функций и оценка коэффициентов _k(х), , должна производиться по априорно известной обучающей выборке, т.е. фактически по результатам подконтрольной эксплуатации объекта (по результатам профилактических испытаний). При этом для снижения ошибок первого и второго рода имеет смысл уменьшить дисперсию случайной величины ε_i путём исключения из массива исходных данных заведомо искажённых выборочных последовательностей. Превышение случайной величины ε_i над регулярной составляющей W(x), t [6.4] может привести к тому, что на анализируемом промежутке времени процесс окажется стационарным по математическому ожиданию, либо при наличии наиболее грубых ошибок изменит направление.

Зависимости диагностических показателей от длительности эксплуатации можно представить в виде линейной регрессионной модели, когда входная переменная х (в нашем случае – срок службы) контролируется без ошибок (дата измерений известна), а выходная переменная y (значение показателя) является случайной величиной. Влияющим фактором будем считать х.

При использовании линейной регрессионной модели результат измерения будет иметь вид [6.5]:

; (6.13)

где: х – фактор (длительность эксплуатации); Y – переменная (отклик); b₀ и b₁ – коэффициенты регрессионного уравнения, подлежащие определению; _i – значение остатков (невязок).

Остатки распределены по нормальному закону: _i  N (0, ²) c M[_i] = 0; D[_i] = ²; cov[_i] = 0.

Для выявления влияния фактора х на изменение средних значений отклика Y выполним дисперсионный анализ линейной регрессии [6.5, 6.6]. Найдем разложение суммы квадратов отклонений случайной переменной y_i от своего среднего значения:

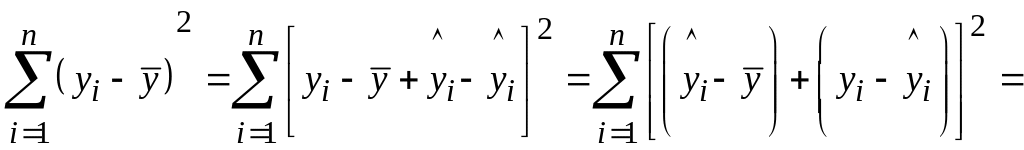
. (6.14)

Учитывая, что – предсказанное значение Y для данного X, подставив в (6.14) второе слагаемое, получим:

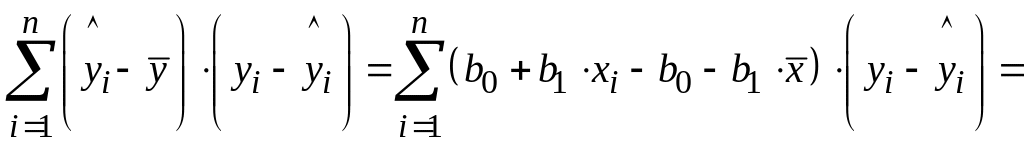
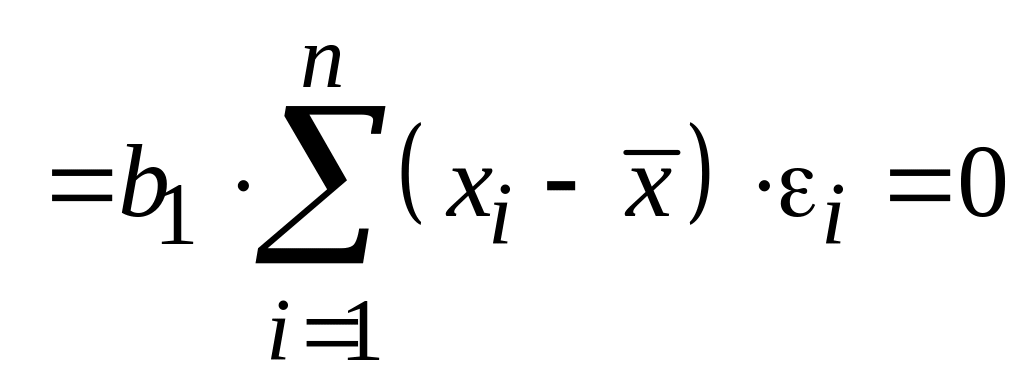. (6.15)

Тогда

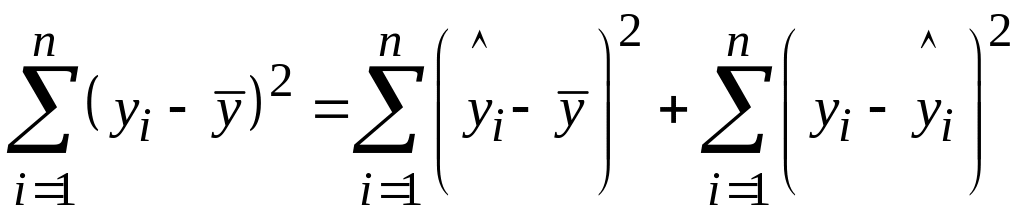. (6.16)

Обозначим:

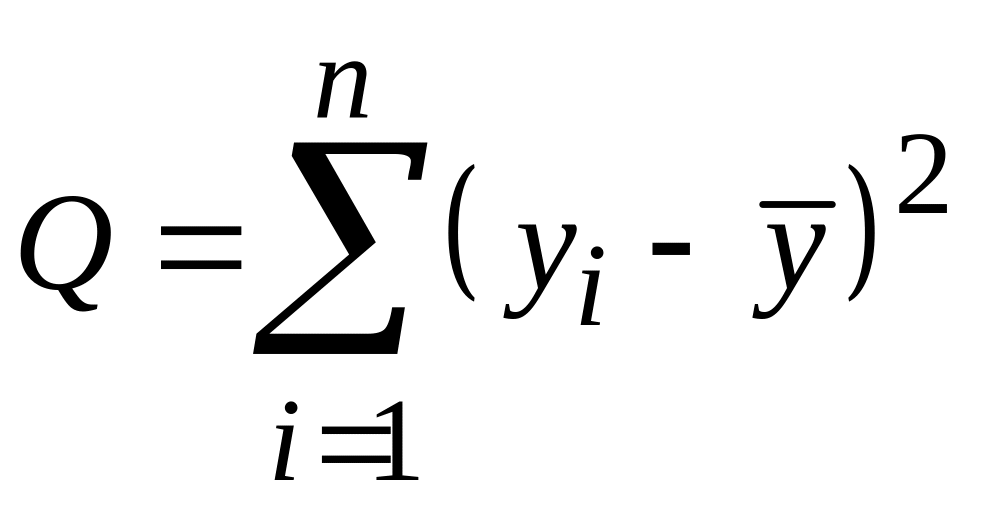– сумма квадратов относительно среднего;

– сумма квадратов, обусловленная регрессией;

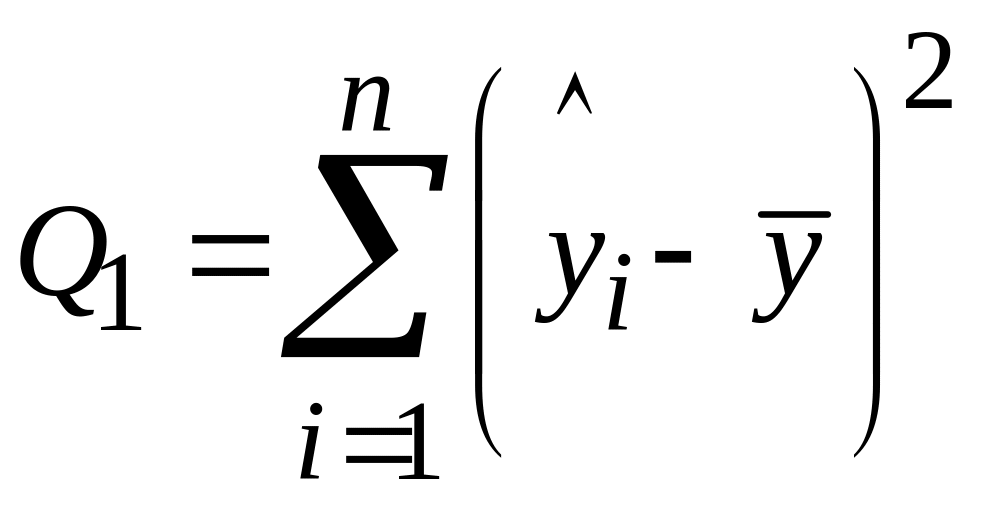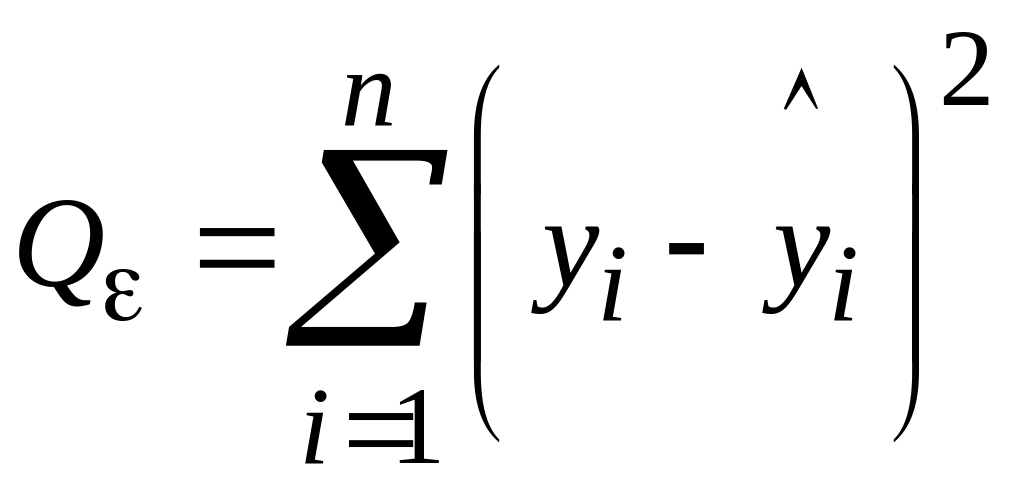– сумма квадратов относительно регрессии.

Тогда

. (6.17)

Рассмотрим модель образования ошибок при вычислении Y_i по Х_i по идеальной модели:

, (6.18)

где _i ~N(0, ²), причем ² неизвестна.

Оценка значения Y_i по принятой модели:

, (6.19)

где: ε_i ~N(0, S²).

Если принятая модель адекватна идеальной, но ² = S², то в противном случае S² > ². Величина S² – это остаточная дисперсия, определяемая суммой квадратов Q_ε. Чем меньше отношение Q_ε/Q, тем более пригодна модель . Для предсказания средних значений Y по Х обычно используют величину [60]

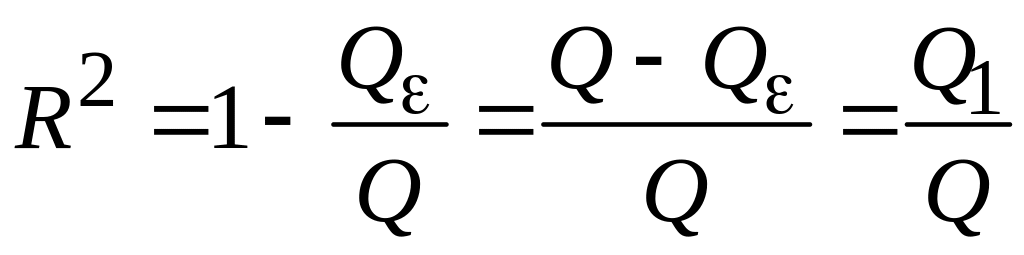. (6.20)

Чем ближе к 1 это отношение, тем лучше выбрана модель (6.20). Разделив числитель и знаменатель (5.20) на (n – 1), получим:

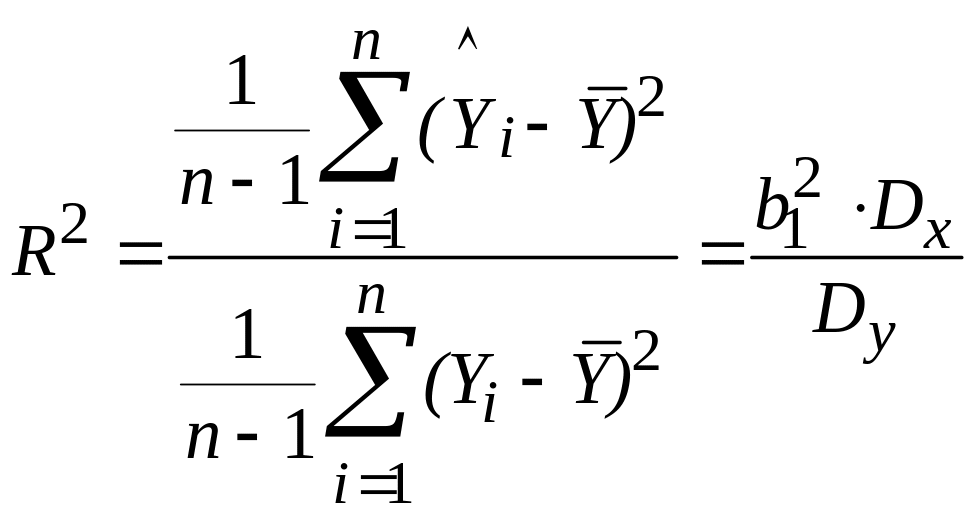. (6.21)

Поскольку Q₁ и Q_ε – функции случайных величин Y_i , то и Q₁, Q_ε – случайные величины.

Математическое ожидание средних квадратов Q₁ и Q_ε будет таким:

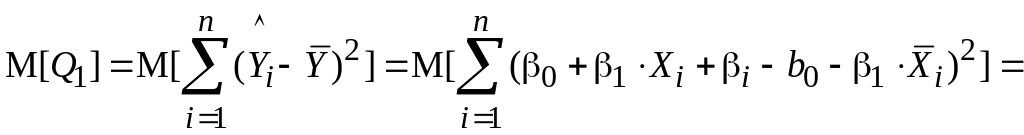
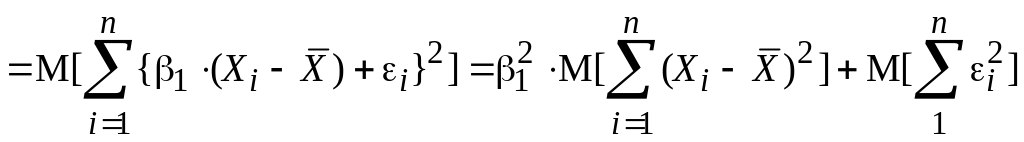. (6.22)

Поскольку Х – не случайная величина, то

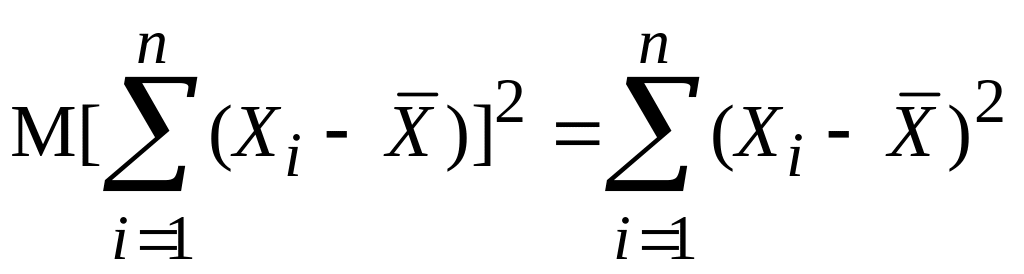; (6.23)

если β₁ = 0, то 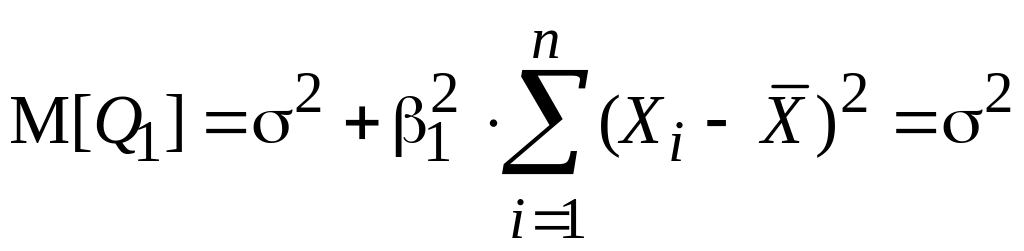; (6.24)

М[S²] = δ². (6.25)

Пусть Н₀ – основная гипотеза (регрессия не значима, т.е. ₁ = 0). Рассмотрим отношение средних квадратов:

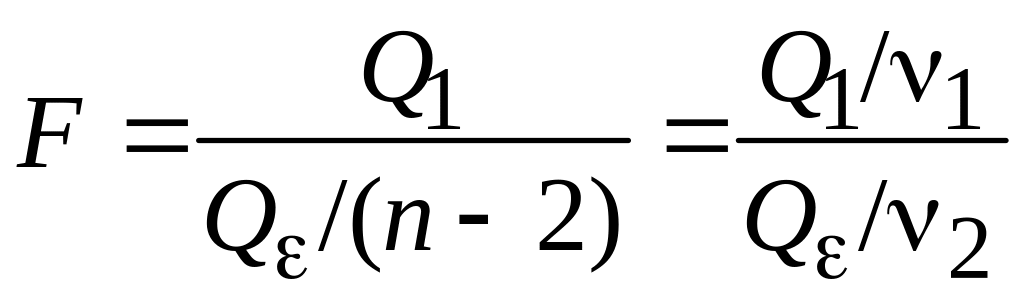, (6.26)

где n – объем выборочных значений; ₁ = 1, ₂ = n – 2 – число степеней свободы.

Тогда

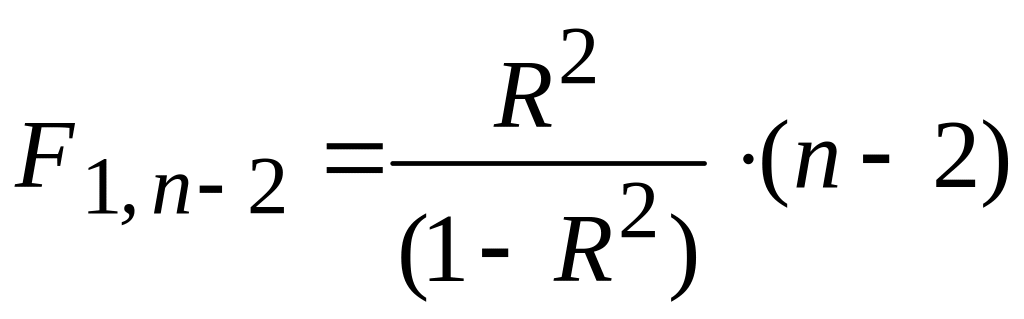; (6.27)

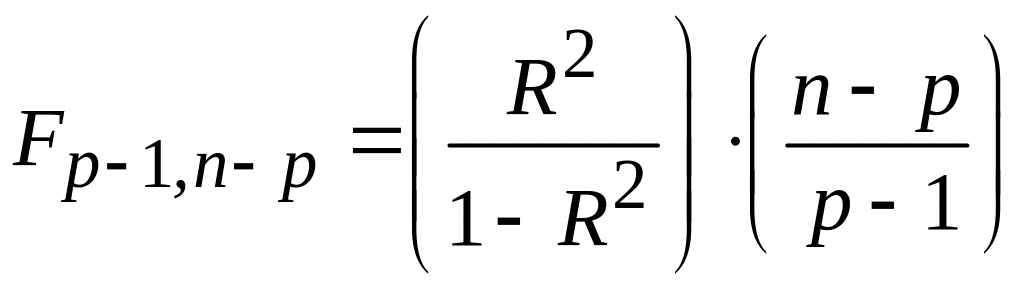, (6.28)

где: p – число слагаемых в регрессионном уравнении.

Математическое ожидание для Q₁/1 и Q_ε /(n – 2) одно и то же и равно δ² (если ₁ = 0). Таким образом, статистика

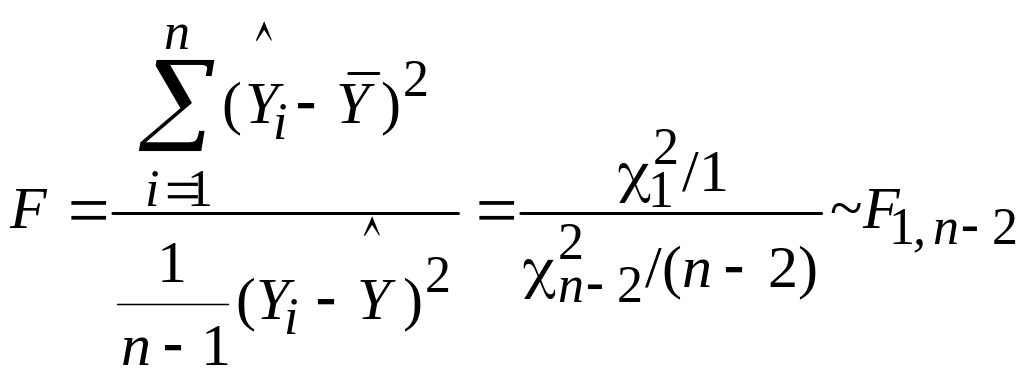. (6.29)

Если U и V – независимые случайные величины с ² распределениями и _{1 ,}₂ степенями свободы, то и .

Порог сравнения F_кр = F_{1 (n–2), (1–)}.

Изменение диагностического признака значимо, если F  F_кр (гипотеза Н₀ отвергается).

Проиллюстрируем использование дисперсионного анализа линейной регрессии для оценки неслучайных отклонений, на примере такого показателя как кислотное число трансформаторных масел.

Проанализируем результаты периодического контроля кислотного числа для двух трансформаторов ПС «Ленинская» Т-1, ON/OB-31,5, 110/35/6 Луганской область и трансформатор ПС «Серп и молот» Т-2, ТДТН-40,5, 110/35/6 Харьковской области. Объем выборки составил 92 значения для трансформатора «Ленинская» Т-1 и 17 значений для трансформатора «Серп и молот» Т-2. Оба трансформатора находятся в эксплуатации более 30 лет. Естественно возникает, задача оценить насколько значимо изменилось значение данного показателя за весь период эксплуатации.

Оценка выполнялась в следующей последовательности:

1. Методом наименьших квадратов определялись коэффициенты линейной регрессии для каждого из трансформаторов:

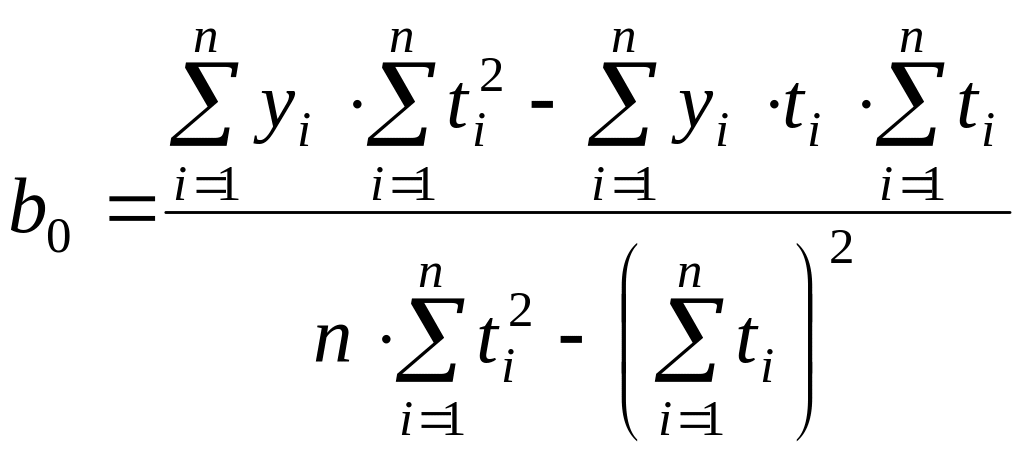; (6.30)

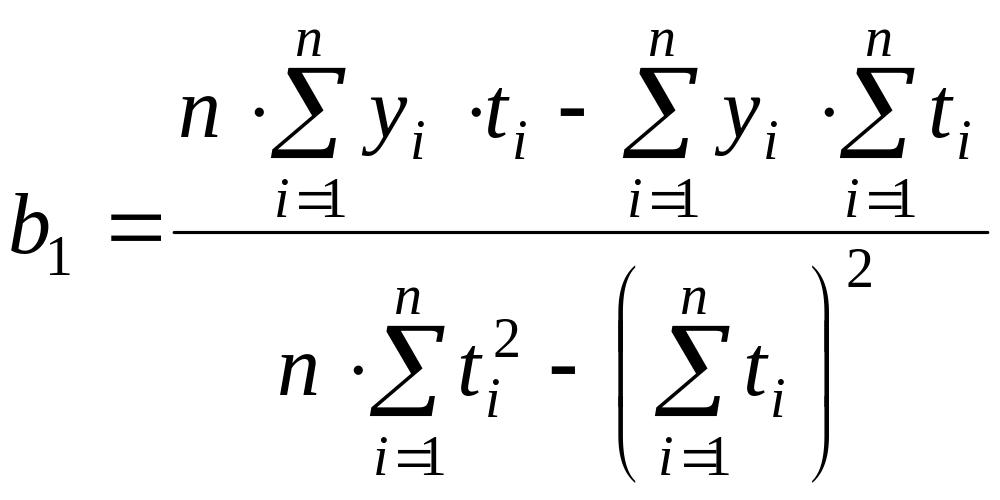. (6.31)

2. Используя выражение (6.19) по (6.21) вычисляем значение величины R² для каждой выборки.

3. Рассчитываем значения критериальных статистик по (5.29).

4. Значения статистик сравнения при ₁ = 1, ₂ = n – 2 и доверительной вероятности р = 0,95, находим по [6.2].

Результаты регрессионного анализа приведены на рисунках 5.2 и 5.3.

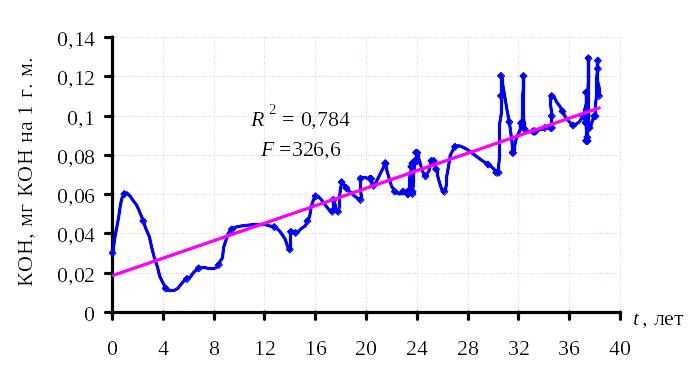
Рисунок 6.2 – Результаты периодического контроля кислотного числа трансформаторных масел и линейная регрессия для ПС «Ленинская» Т-1

Для оценки значимости изменений кислотного числа в данных трансформаторах выполним сравнение рассчитанных значений критерия Фишера с критическими точками.

Для трансформатора ПС «Ленинская» Т-1 расчетное значение критерия Фишера F=326,6 превышает критическое значение , что свидетельствует о интенсивном окислении масла, в данном трансформаторе, необходимо принять меры по ингибированию окислительных реакций, например, сушка масла, его регенерация, замена силикагеля или добавление антиокислительных присадок (ионол).

Для трансформатора ПС «Серп и молот» Т-2 расчетное значение критерия Фишера F=1,416 не превышает критическое значение , что свидетельствует о том, что накопление в масле органических кислот происходит не так интенсивно. Как видно из рисунка 5.3 это обусловлено выполненным оперативным персоналом ингибированием окислительных реакций после 12 и 24 лет эксплуатации.

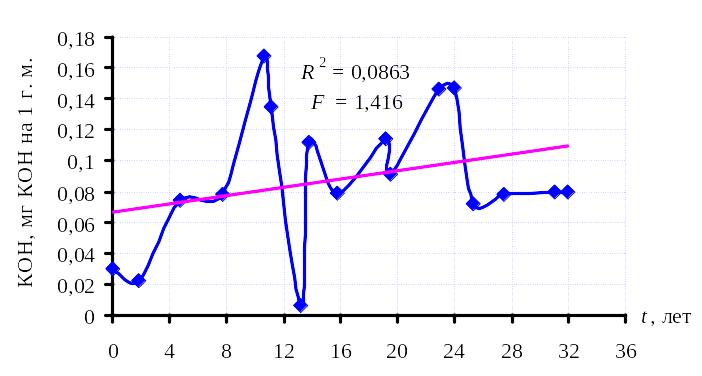
Рисунок 6.3 – Результаты периодического контроля кислотного числа трансформаторных масел и линейная регрессия для ПС «Серп и молот» Т-2

При использовании данного метода следует учитывать, что в случае значимого отклонения зависимости диагностического показателя от линейной зависимости, метод может давать существенную погрешность, поскольку сумма квадратов отклонений от среднего, обусловленная отклонением от линейности будет входить в остаточную сумму квадратов. Если по известной априорной информации или в результате выполненного дисперсионного анализа на отклонение от линейности [6.6, 6.7], установлена значимая нелинейность показателя, то целесообразно использовать математические модели дисперсионного анализа [6.6, 6.7].