6 Методы распознавания кривых

Во многих случаях информация о состоянии системы (объекта) содержится в виде записи значений диагностического параметра или его отклонений от нормального или первоначального уровня в различные моменты времени [6.1]. Результаты представляются в виде непрерывных функций x (кривых) или совокупности дискретных значений Принципиальной разницы между этими двумя видами информации нет и, ограничиваясь некоторой максимальной частотой периодической составляющей, можно указать шаг квантования, при котором за период наблюдения Т непрерывная и дискретная формы записи эквивалентны. В других случаях дискретное представление можно рассматривать как приближенное.

Разберем непрерывную запись диагностического параметра в виде кривой . Наличие неисправности может проявиться в росте отдельных периодических составляющих в спектральном составе, в существенном изменении значений диагностического параметра и т. п. Анализируя протекания кривой , можно во многих случаях сделать важные заключения о техническом состоянии системы (объекта). Установление соответствия между состоянием системы и протеканием отображающих функций будем называть распознаванием кривых.

Для технической диагностики представляет интерес решение двух основных вопросов.

1. Являются ли наблюдаемые во время эксплуатации изменения кривой следствием случайных, несущественных изменений в системе или они вызваны более серьезными причинами.

2. Если отличия в протекании кривой являются значительными, то с какими из возможных состояний системы они связаны. При непрерывном слежении за параметрами системы вторая задача решается после первой, при выборочном наблюдении или анализе указанные задачи независимы.

Основная идея методов распознавания кривых состоит в отображении бесконечного многообразия значений функций в конечномерное пространство признаков.

Различные методы распознавания отличаются выбором системы признаков и способами разделения состояний в пространстве признаков.

6.1 Обнаружение неслучайных отклонений по методу средних

Рассмотрим на примере такого диагностического признака, как тангенс угла диэлектрических потерь трансформаторных масел. Данный показатель является одной из важнейших характеристик, состояния трансформаторных масел, значения которого определяются в результате периодических испытаний. В качестве примера, рассмотрим трансформатор ПС «Вентиляционная» Т-3, ТДНГ 20, 110/10. Зависимость тангенса угла диэлектрических потерь масла от продолжительности эксплуатации, приведена на рис. 6.1. Пусть анализируются данные за два периода k и l (рис. 6.1).

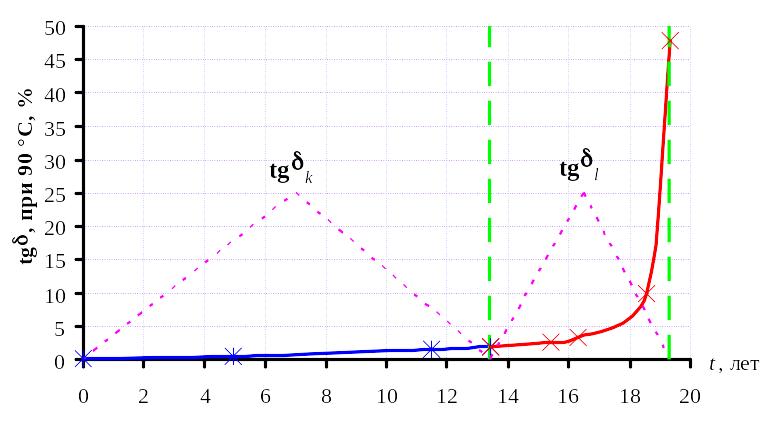
Рисунок 6.1 – Обнаружение систематических отклонений по выборочным данным

Сопоставляются совокупность n_k значений параметра tgδ (выборка {tgδ_k}) и совокупность n_l значений за другой отрезок времени (выборка {tgδ_l}). Тем самым поведение кривой на двух участках описывается конечным числом признаков – ординатами кривой. Обычно эти ординаты выбирают в виде последовательных, равноотстоящих по времени значений tgδ(t). Существует довольно большое число способов оценки различия двух выборок [6.1, 6.2]. Одним из наиболее простых и эффективных является метод средних, в соответствии с которым определяется среднее значение и среднеквадратичное отклонение каждой из выборок:

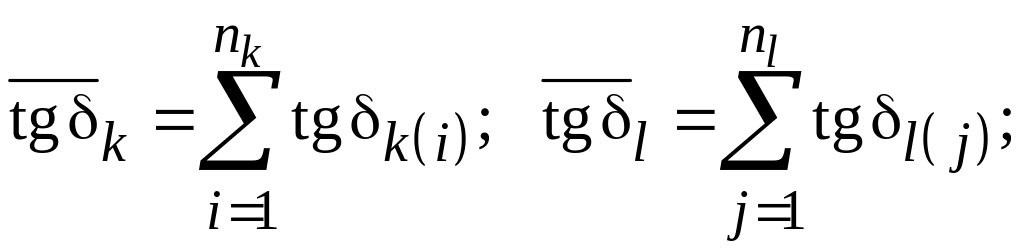(6.1)

(6.2)

Далее оценивается значимость различия с помощью критерия Стьюдента [6.2]:

(6.3)

Различие признается значимым если:

(6.4)

где: – коэффициент Стьюдента для числа степеней свободы и доверительной вероятности α.

Разобьем анализируемую выборку на два участка (см. рис. 6.1) по 4 значения на каждом и определим средние значения и значения средне квадратических отклонений на участках:

Определяем расчетное значение критерия Стьюдента по выражению (6.3): . Задаемся уровнем значимости α=5% и находим из [6.2] критическое значение критерия Стьюдента, для заданного уровня значимости α, и числа степеней свободы n=6:

Поскольку расчетное значение критерия Стьюдента, меньше табличного, то изменения математического ожидания тангенса угла диэлектрических потерь, можно считать значимым.

Для оценки различия выборок иногда используется простой критерий Фишера (отношение дисперсий)

(6.5)

Различие признается значимым если:

(6.6)

где: – критическое значение критерия Фишера для числа степеней свободы: ; и доверительной вероятности α.

Однако, применение критерия Фишера эффективно только в случаях, когда отличие выборок сказывается в нестабильности диагностического параметра при почти неизменном среднем значении.

Проверим анализируемую выборку на значимость расхождений по дисперсиям. Для этого рассчитываем значения дисперсий на участках, и определяем расчетное значение критерия Фишера

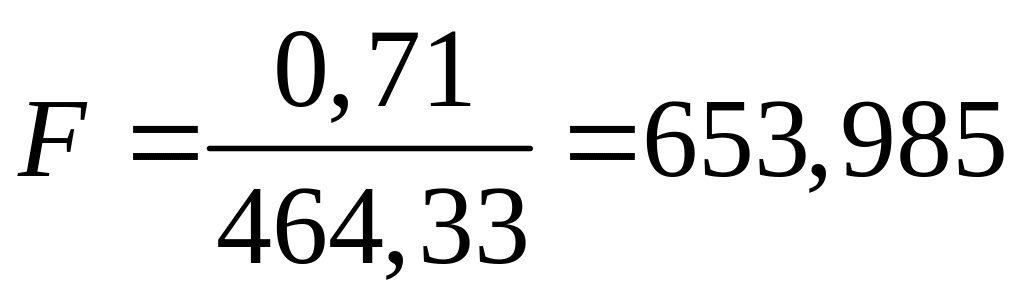
Задаемся уровнем значимости α=5% и находим из [6.2] критическое значение критерия Фишера, для заданного уровня значимости α, и числа степеней свободы n₁=3 и n₂=3:

Поскольку расчетное значение критерия Фишера, меньше табличного, то изменения дисперсии тангенса угла диэлектрических потерь, можно считать значимым. Полученные результаты, свидетельствуют о том, что в изоляции трансформатора Вентиляционная» Т-3, происходит интенсивный процесс старения, необходимо вмешательство персонала