5.5 Распознавание траектории изменения состояния диагностируемого объекта

Влияние внешних и внутренних факторов приводит к тому, что с течением времени состояние технических объектов изменяется. При этом показатели характеристик или параметры можно рассматривать как функции времени, представляющие собой траектории, описывающие перемещения этих величин с течением времени. Если есть возможность заранее определить и задать эталонные траектории, то, сравнивая действительные траектории с эталонными, можно установить, к какому из классов относится объект по своему состоянию. Эталонные траектории, характеризующие изменения состояния конкретных объектов, можно получить в результате либо длительного наблюдения за поведением подобных объектов в период эксплуатации, либо физического пли математического моделирования процессов, протекающих в объекте с течением времени. Таким образом, определение состояния объектов в этом случае сходно с задачей распознавания образов, определяемых траекториями показаний или параметров [5.9].

Рассмотрим некоторые особенности решения задачи распознавания траектории изменения состояния (работоспособности) объекта диагностики. Пусть В_1, ..., В_т – множество эталонных траекторий, характеризующихся определенной степенью работоспособности, т. е. траектории соответствуют определенным классам объектов, в частности, может быть: B₁ R₁, ..., В_λ R_2, ..., B_m R_m; ξ₁, ..., ξ_k – множество признаков отдельной траектории в каждый момент времени; ξ_s(i), s = 1, 2, …, k, i =1, 2, ..., п – множество значений s-гo признака траектории, где i – выбранные моменты времени; A(ξ_а1(i), ..., ξ_аk (i)), i =1, 2, ..., п – траектория изменения состояния объекта. Необходимо в процессе решения задачи распознать траекторию А, т. е. отнести ее к наиболее близкой ей эталонной траектории.

Назовем интервалом D_AВ между траекториями А и В положительную величину, квадрат которой определяется выражением [5.9]:

(5.44)

Пусть множество признаков траекторий представляет собой бинарную последовательность, т. е. ξ_s(i) равно либо 1, либо 0. Отсюда

(5.45)

Таким образом, если рассматривать совокупность ξ_s(i), s = l, ..., k, i =1, ..., п как [k n ]-разрядное двоичное число, то квадрат интервала между траекториями А и В будет равен количеству поразрядных несов падений в двух [k n ]-разрядных двоичных числах А (ξ_аs (1), …, ξ_аs (n)) и В (ξ_аs (1), …, ξ_аs (n)):

(5.46)

Выражение (5.44) удовлетворяет следующим топологическим условиям:

D_АВ = D_ВА, D_АВ = D_АС + D_СВ, D_АВ ≥ 0, (5.47)

причем D_AB = 0 тогда и только тогда, когда А соппадает с В.

Каждая траектория В_λ, определяемая некоторым множеством признаков в пространстве признаков, будет занимать определенную область, которую можно характеризовать величиной диаметра D_λ этого множества. Диаметром множества можно, в частности, считать наибольшее расстояние между двумя его точками, т.е. величину, пропорциональную мере множества в i-ом временном сечении:

, (5.48)

(5.49)

где – мера множества В_λ в i-й момент времени, N – число траекторий, принадлежащих В_λ; – центр множества В_λ по s-му параметру:

(5.50)

Коэффициент γ зависит от закона распределения точек множества в пространстве признаков и точности, с которой желательно определить границу множества В_λ.

Определим меру близости и центр множества через условные вероятности появления множества {ξ} s-го параметра в i-м временном сечении, принадлежащего В_λ:

Так как ξ_λsr равно либо 1, либо 0, и при увеличении N, согласно закону больших чисел, частота события стремится к ее вероятности, можно записать

(5.51)

Пользуясь выражениями (5.50) и (5.51), можно определить координаты s= l, 2, ..., k центра области В_λ:

(5.52)

Произведем некоторые преобразования в выражении меры множества (5.49), которая представляет собой средний квадрат отклонения точек множества от его центра:

Так как ξ_sr(i) может быть равным либо 1, либо 0, то

Тогда

или

Наконец, имея в виду выражение (5.69), можем записать

и окончательно получить

(5.53)

Формулы (5.52) и (5.53) позволяют определить центр и меру в i-м сечении каждой траектории В_λ.

Введем критерий различимости траекторий. Это понятие весьма существенно, ибо, чем меньше интервал D_ВλВl между центрами двух областей и чем больше их диаметр, тем больше эти области перекрывают друг друга и тем большее число точек можно с равным основанием отнести как к одной области, так и к другой.

Критерий различимости двух траектории можно выразить следующим образом [5.9]:

(5.54)

В соответствии с (5.44) и (5.52) или .

Метод распознавания траекторий изменения состояния (работоспособности) технических объектов может оказаться весьма эффективным в тех случаях, когда имеется априорная информация об эталонных траекториях и по каким-либо причинам невозможно применить для решения задачи прогнозирования аналитические и вероятностные методы и методы статистического распознавания образов.

Сформулируем общую процедуру оценки степени старения масла с помощью метода распознавания траекторий [5.10–5.12]. Учитывая, что одним из важнейших факторов, который определяет интенсивность окислительных процессов, является температура изоляции, которая в свою очередь, зависит от загрузки трансформаторов [5.13–5.14], процедура оценки имеет вид:

Диагностируемый временной ряд проверяется на принадлежность одновременно трем эталонным траекториям. При этом первая траектория имеет среднюю загрузку равную средней загрузке диагностируемого трансформатора, вторая – ближайшую большую, третья ближайшую – меньшую.

Решение: если диагностируемый ряд принадлежит первой траектории, то старение масла считается нормальным.

Если диагностируемый временной ряд принадлежит траектории с более высоким значением средней загрузки, то вне зависимости от того превысило значение показателя граничное значение или нет, старение считается аномальным и рекомендуется применить меры по ингибированию процессов старения (замена силикагеля, сушка, добавка антиокислительных присадок, регенерация масла и т.д.).

Если же диагностируемый временной ряд показателя принадлежит подмножеству с меньшим значением средней мощности, то выясняются причины, по которым произошло снижение значения показателя. Т.е. является ли снижение значения показателя следствием оперативного вмешательства персонала или же произошла ошибка при отборе проб масла и проведении испытаний.

На рисунке 5.8 приведены диаметры и центры траекторий кислотного числа трансформаторных масел.

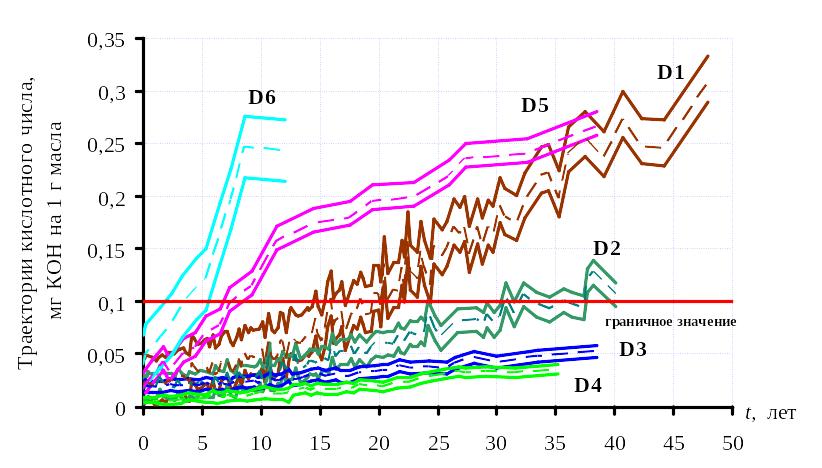
Рисунок 5.8 – Диаметры и центры траекторий для подмножеств кислотного числа трансформаторного масла.

В качестве диагностической меры расстояния будем использовать величину L, характеризующую расстояние между диагностируемой траекторией и центрами ближайших эталонных траекторий. Поскольку распознавание проводится по каждому из показателей в отдельности, то можно использовать евклидово пространство и тогда расстояние между точкой a на диагностируемой траектории и центром эталонной траектории точкой x в j-ый момент времени определяется как:

,

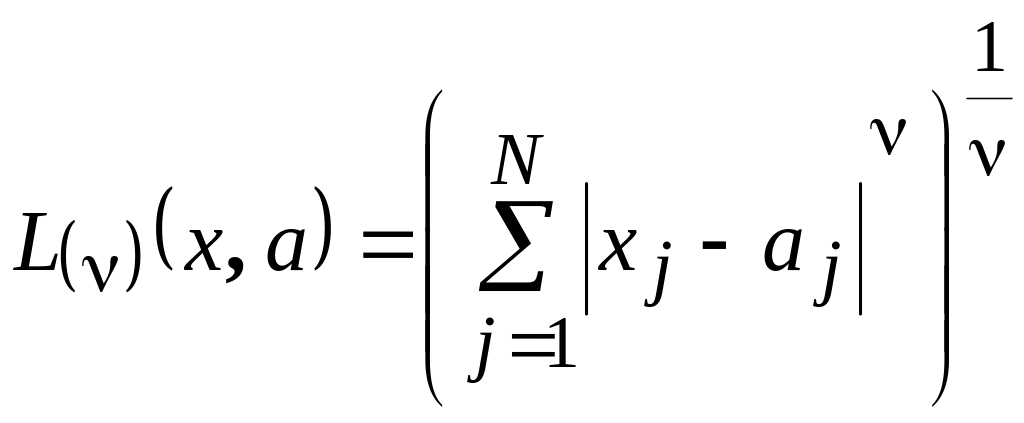где:  – мера расстояния;

Диагностируемая траектория относится к одной из эталонных, если выполняется условие:

Надежность распознавания в этом случае будет тем выше, чем меньше расстояние L_i по сравнению с другими расстояниями. Это можно охарактеризовать коэффициентом распознавания:

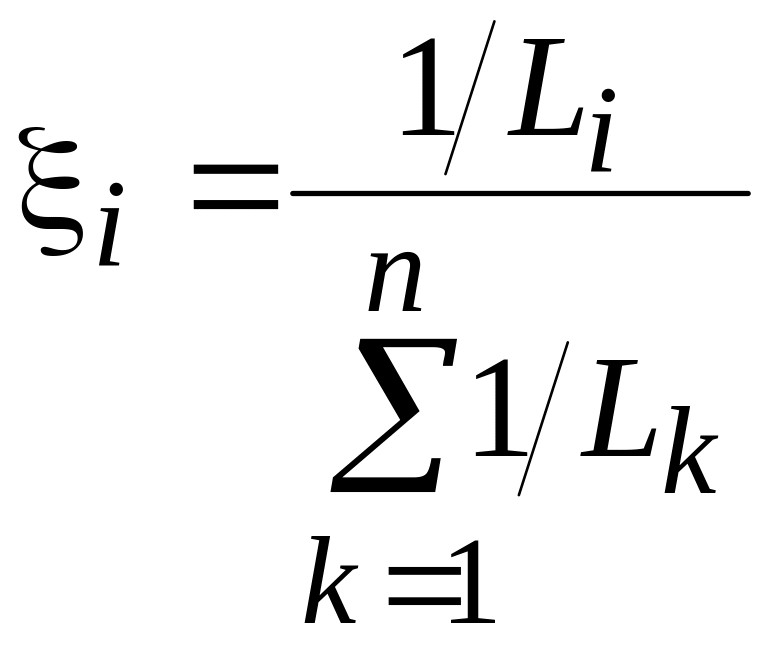
Проиллюстрируем реализацию разработанного метода на примере кислотного числа масла трансформаторов ПС «Биологическая» Т-1 и ПС «Орджоникидзе» Т-2, АК «Харьковоблэнерго» [5.10]. По результатам последних испытаний значения кислотного число составило для трансформатора ПС «Биологическая» Т-1 – 0,065 мг КОН, через 14,5 лет эксплуатации, а для трансформатора ПС «Орджоникидзе» Т-2 – 0,022 мг КОН, через 14 лет эксплуатации. Согласно, действующей методики значения кислотного числа в этих трансформаторах меньше граничного и находятся в норме. Средняя загрузка данных трансформаторов за 13 лет, составила 5,5 % и 11 % соответственно. Следовательно, временные ряды кислотного числа масла должны принадлежать траектории D3. Зависимости кислотного числа трансформаторного масла и границы трех ближайших траекторий приведены на рис. 5.9. Как видно из рисунка значение кислотного числа масла трансформатора «Биологическая» Т-1 вышло за пределы траектории D3, а для трансформатора «Орджоникидзе» Т-2 находится в пределах данной траектории. Выполненный расчет расстояний между последним результатом измерений кислотного числа масла и центрами эталонных траекторий дал следующие результаты. Для трансформатора «Биологическая» Т-1 L2=0,027, L3=0,034, L4=0,047 мг КОН. Для трансформатора «Орджоникидзе» Т-2: L2=0,017, L3=0,001, L4=0,005 мг КОН. Сравнив значения рассчитанных диагностических расстояний, видим, что для классификации трансформатора «Биологическая» Т-1 трех траекторий явно недостаточно.

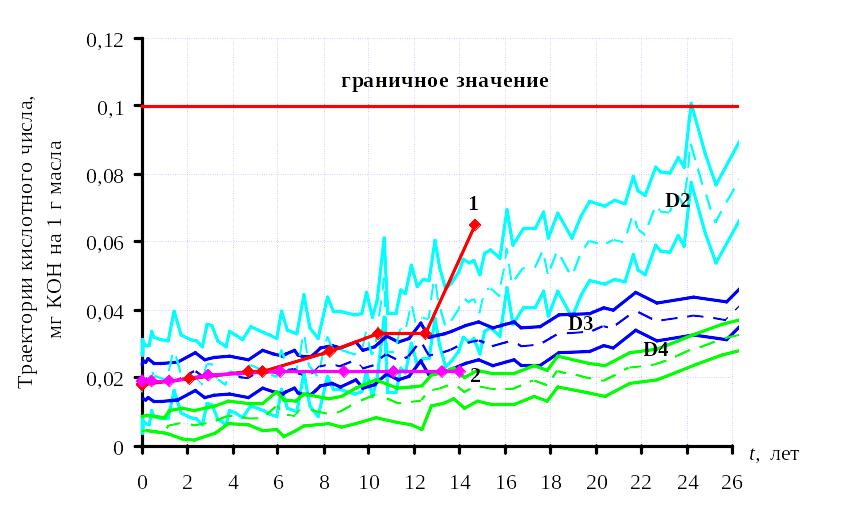
Рисунок 5.9 – Зависимости кислотного числа трансформаторного масла от длительности эксплуатации для диагностируемых трансформаторов, диаметры и центры трех ближайших траекторий.

Рассчитаем расстояние от центра траектории D1 (ближайшая большая к траектории D2) до последнего результата измерений кислотного числа диагностируемых трансформаторов. Для трансформатора «Биологическая» Т-1: L1=0,003 мг КОН, для трансформатора «Орджоникидзе» Т-2: L1=0,045 мг КОН. Выбираем из всех полученных диагностических расстояний минимальные, для трансформатора «Биологическая» Т-1 это L1, а для трансформатора «Орджоникидзе» Т-2 это L3. Определим коэффициент распознавания (при диагностической мере первого порядка) для трансформатора «Биологическая» Т-1:

.

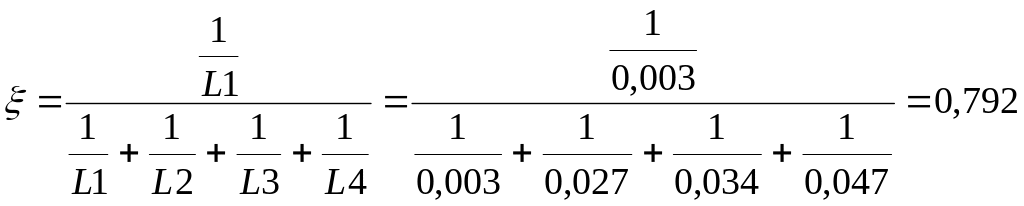Для трансформатора «Орджоникидзе» Т-2:

.

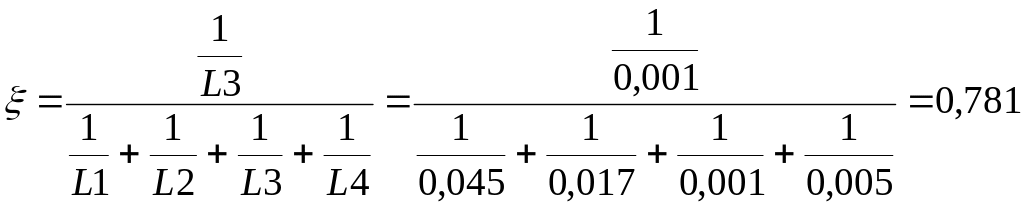Таким образом, трансформатор «Орджоникидзе» Т-2 следует отнести к траектории D3 при уровне распознавания 0,78, а трансформатор «Биологическая» Т-1 к траектории D1 при уровне распознавания 0,79. На рис. 5.10 приведены зависимости уровней распознавания от меры расстояния, полученные для этих трансформаторов.

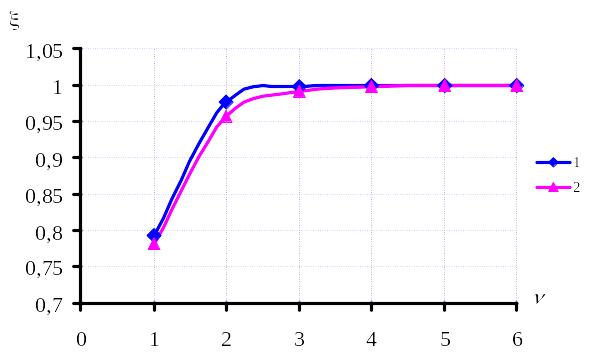
1 – трансформатор ПС «Биологическая» Т-1;

2 – трансформатор ПС«Орджоникидзе» Т-2

Рисунок 5.10 – Зависимости уровней распознавания от меры расстояния, полученные для трансформаторов:

Из них видно, что наиболее оптимальными являются квадратичная и кубическая мера расстояния, использование которых позволяет получить максимальное значение уровней распознавания. Дальнейшее же увеличение значения меры расстояния не приводит к росту значение уровней распознавания.

Из выполненных расчетов следует, что окисление масла в трансформаторе «Орджоникидзе» Т-2 протекает с нормальной скоростью, повода для вмешательства нет. Для трансформатора «Биологическая» Т-1 окисление масла признается аномальным (при загрузке трансформатора 5,5 %, старение происходит с той же интенсивностью, как и для трансформаторов с загрузкой 50 %) требуется оперативное вмешательство. Приведенный пример наглядно демонстрирует преимущества предлагаемого метода оценки старения масла по сравнению с традиционным [5.15]. Разработанный метод оценки старения масла позволяет количественно оценить динамику дрейфа показателей, даже если значения этих показателей находятся в области допустимых значений.

В заключение отметим еще один способ решения задачи прогнозирования с использованием так называемого метода функции отказов. Суть метода заключается в следующем. Все отказы объектов упорядочиваются по времени их возникновения τ_i: τ₁, τ₂, ... τ_N, где τ₁ < τ₂ < ... <τ_N и N – количество отказов. Каждому объекту, отказавшему в момент τ_i, очевидно, в начальный момент времени соответствует совокупность параметров {ξ}_i ={ξ₁, ξ₂, …, ξ_k}_i, т. е. {ξ}₁, {ξ}₂, …,{ξ}_N или векторы ξ₁, ξ₂, …, ξ_N.

Применяя предположение (которое уже использовалось в методах статистической классификации), что значение векторов состояния ξ соответствуют определенным образом подготовленности объектов, можно говорить о зависимости вектора состояния ξ от времени отказа объекта τ. В общем случае ξ = φ (τ_i) – нелинейная функция и в связи с этим возникает задача аппроксимации ее простейшими функциями, например, вида

(5.55)

где v – весовые коэффициенты, которые определяются из условия минимизации средней квадратической ошибки отклонения.

Существенным достоинством этого метода является то, что он может быть заложен в простую опознающую систему.