5.4 Формирование эталонных множеств в условиях временного дрейфа диагностических признаков.

В предыдущих разделах эталонные образцы, формировались из условия, что значения диагностических признаков не изменяются во времени и зависят только от состояния диагностируемого объекта. Однако, на практике возникают задачи классификации объектов, которые находятся в области одного диагноза но имеют различную степень износа. Такие задачи, возникают при диагностике длительно развивающихся процессов старения изоляции. Например, для оценки степени полимеризации целлюлозы или степени окисления трансформаторных масел. Характерной особенностью таких процессов является изменение (дрейф) математических ожиданий показателей во времени. Задача формирования эталонного образца усложняется тем, что скорость дрейфа показателей зависит от условий эксплуатации оборудования, которые не всегда известны, особенно для оборудования длительное время находящегося в эксплуатации. Поэтому задачу формирования эталонного образца необходимо решать с точки зрения, статистической обработки результатов испытаний.

Условием того, что в данной группе объекта скорость старения одинакова, является минимальный разброс между показателями в каждый момент времени. Для количественной оценки близости зависимостей показателей использовалось выборочное корреляционное отношение [5.6], которое служит для оценки тесноты нелинейной корреляционной связи между величинами Х и Y. Рассмотрим дисперсию случайной величины Y, которую можно представить в виде двух составляющих:

. (5.33)

Первая составляющая в правой части выражения (5.33)

. (5.34)

есть средней условной дисперсией, которая характеризует степень рассеивания случайной величины Y относительно кривой регрессии. Вторая составляющая (5.33) есть систематическая составляющая общей дисперсии величины Y, которая характеризует отклонение кривой регрессии, аппроксимирующей нелинейную зависимость от математического ожидания. Таким образом, имеем, что:

. (5.35)

Корреляционное отношение определяется как

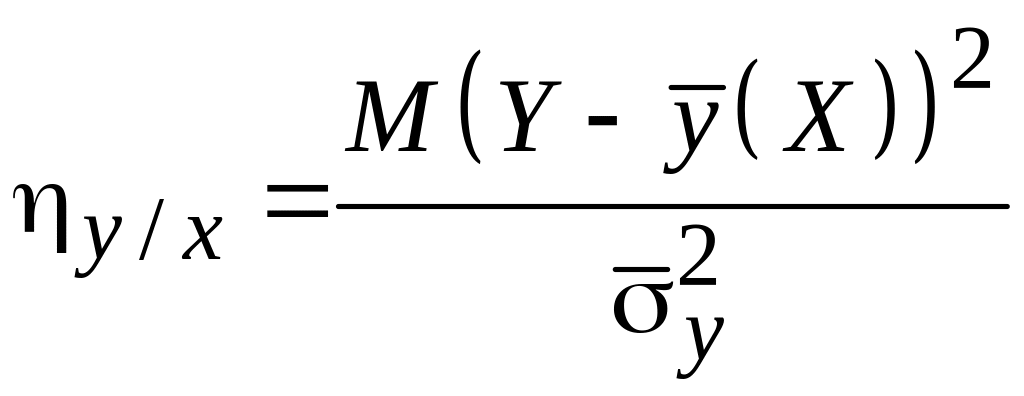(5.36)

и показывает, какую часть в общей дисперсии занимает систематическая составляющая. Учитывая, что

. (5.37)

Окончательно имеем:

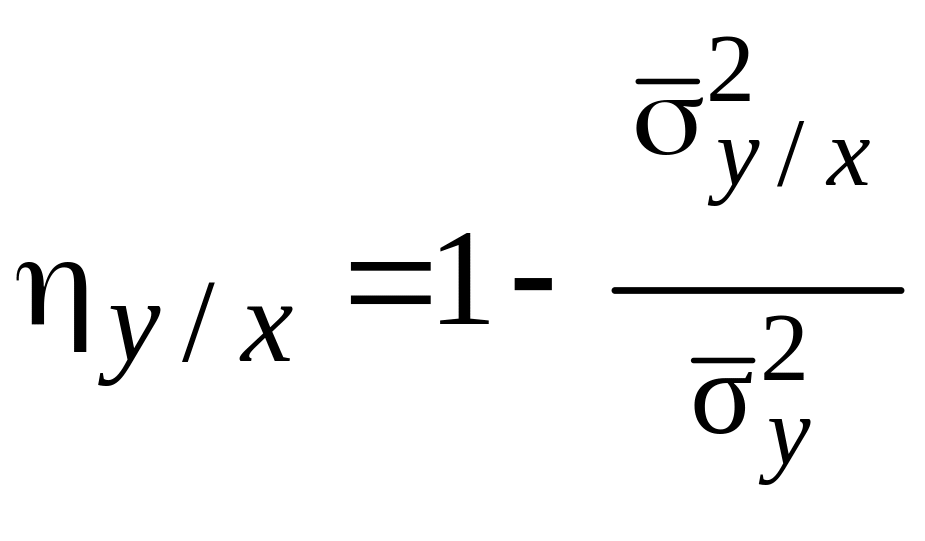(5.38)

На практике для оценки эмпирического корреляционного отношения используется следующее выражение:

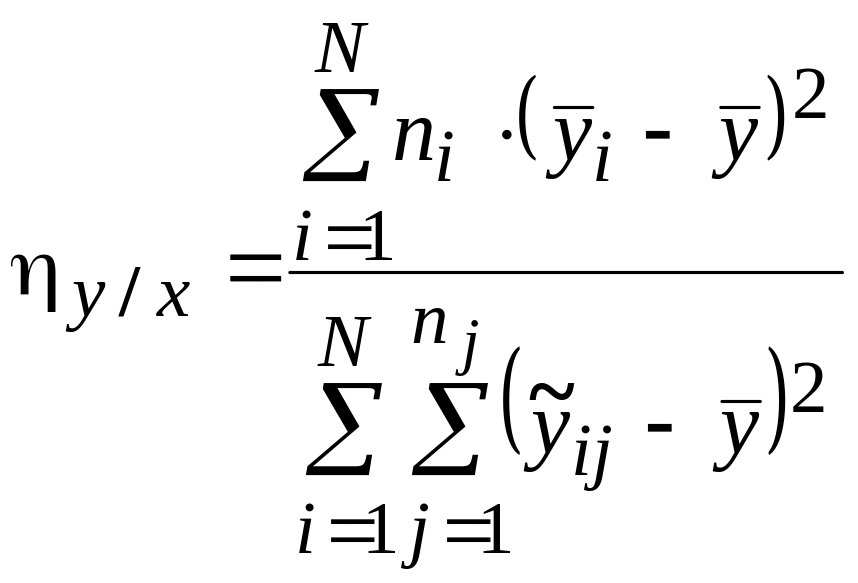(5.39)

где: N – объем выборки; – условное среднее, полученное для значений x_i при ; – общее среднее по всем экспериментальным точкам; – результаты наблюдений в i-той экспериментальной точке.

Использование величины корреляционного отношения в качестве меры близости зависимостей показателей, можно обосновать с точки зрения следующих позиций. Поскольку все значения величины Y разбиты на группы, то можно представить общую дисперсию признака в виде суммы внутригрупповой и межгрупповой дисперсий [5.6]:

. (5.40)

Преобразуем выражение (5.57):

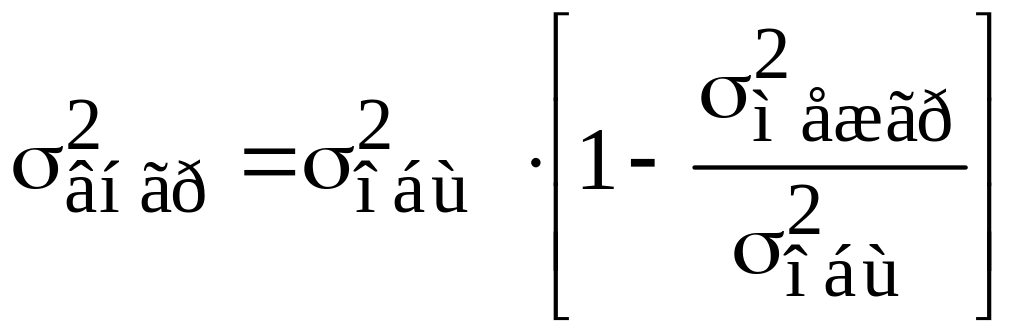. (5.41)

или

. (5.42)

Как видно из (5.42), если , то , и, следовательно, стремится к нулю каждая из групповых дисперсий, что, естественно, говорит о повышении однородности общего массива данных. Таким образом, задача формирования эталонного образца сводится к отысканию такой комбинации временных зависимостей показателей, которая бы обеспечивала максимальное значение корреляционного отношения на заданном временном интервале.

Проиллюстрируем предложенный способ на примере такого показателя как кислотное число трансформаторных масел [5.7, 5.8]. Исходная выборка представляет собой результаты периодического контроля данного показателя в трансформаторах 110 кВ по Донецкой, Луганской, Полтавской, Сумской, Харьковской областям Украины и АР Крым. Всего проанализировано результаты испытаний по 231 трансформатору, объем анализируемой выборки составил 3741 значение.

Формирование групп трансформаторов с одинаковой скоростью окисления масел (эталонных объектов) выполнялось в следующей последовательности:

1. Результаты наблюдений представлялись в виде временных рядов, т.е. двумерных массивов: длительность эксплуатации – показатель;

2. Для каждого временного ряда показателя качества масла массива исходных данных Мa рассчитывали значения коэффициентов парной корреляции:

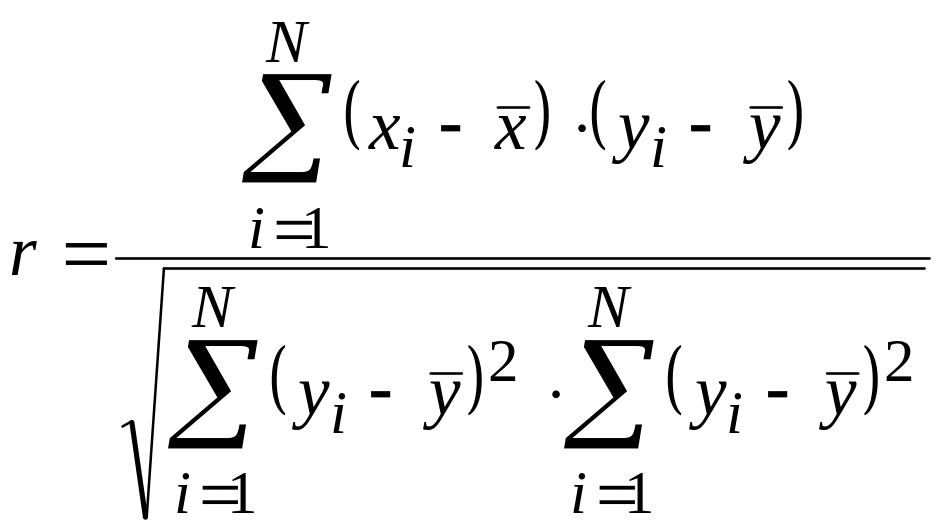. (5.43)

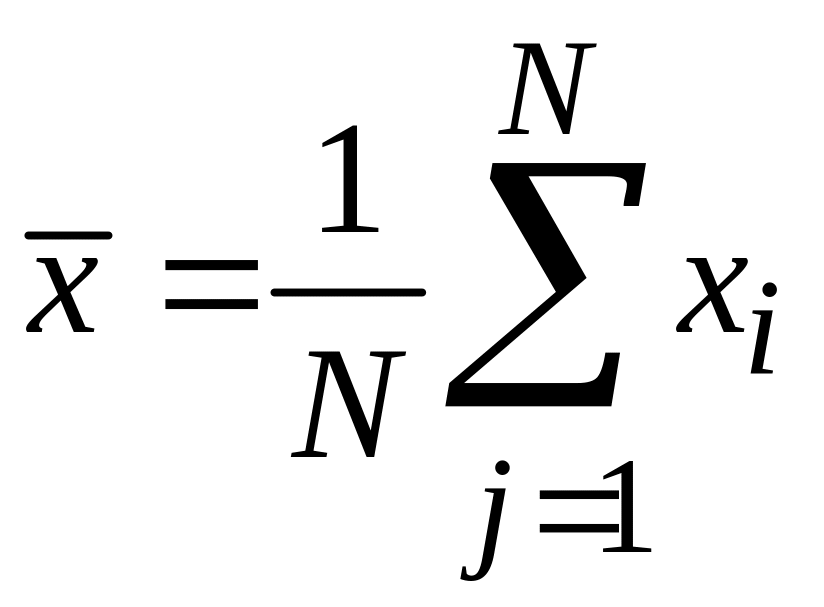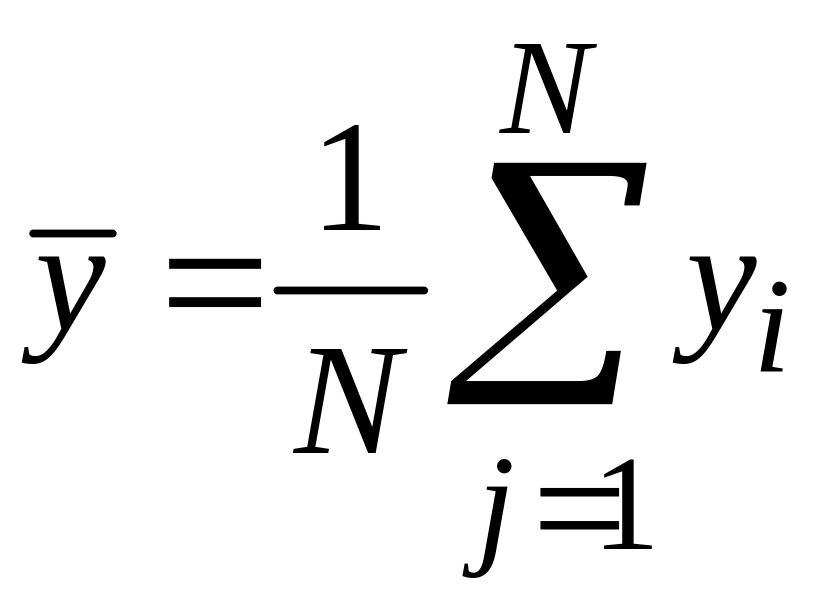где: x_i – текущее значение времени эксплуатации; y_i – текущее значение показателя; – математическое ожидание времени эксплуатации; – математическое ожидание показателя; N – объем выборочных значений в данном временном ряде.

3. Полученные значения коэффициентов парной корреляции ранжировались по убыванию;

4. В качестве базового ряда выбирали временной ряд показателя, для которого наблюдалось максимальное значение коэффициента парной корреляции на наибольшем интервале наблюдений;

5. К базовому ряду добавляли следующий ряд, имеющий максимальное значение коэффициента парной корреляции, и определяли корреляционное отношение объединенного ряда;

6. В случае, если значение корреляционного отношения объединенного ряда уменьшалось, ряды признавали неоднородными и к базовому добавляли следующий ряд;

7. После выполнения проверки базового ряда с последним рядом в массиве исследуемого показателя формировали следующий массив однородных данных этого же показателя из тех данных, которые не вошли в предыдущий массив, в аналогичной последовательности.

Результаты расчетов для анализируемого массива кислотного числа приведены в таблице 5.2. Анализ результатов табл. 5.2 позволяет сделать вывод:

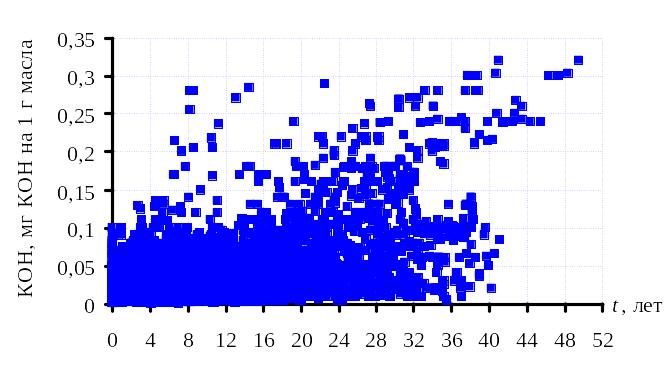
1. Значения коэффициентов парной корреляции и корреляционного отношения кислотного числа из массивов, полученных по критерию максимума корреляционного отношения (М1-М6), значительно превосходят аналогичные значения из массива Ma. Это свидетельствует о высокой эффективности метода выделения групп трансформаторов с одинаковой скоростью дрейфа показателей (см. рис. 5.7).

Таблица 5.2 – Значения коэффициента парной корреляции и корреляционного отношения между кислотным числом масла и длительностью эксплуатации

Показатель качества масла	Массив	n	N	Коэффициент парной корреляции ρy-t	Корреляционное отношение
					ηt/y	ηy/t
Кислотное число	Ma	231	3741	0,535	0,658	0,661
	М-1	49	951	0,920	0,943	0,944
	М-2	49	801	0,901	0,926	0,920
	М-3	33	349	0,900	0,924	0,920
	М-4	16	250	0,918	0,931	0,936
	М-5	4	96	0,906	0,949	0,939
	М-6	3	49	0,928	0,946	0,934

а

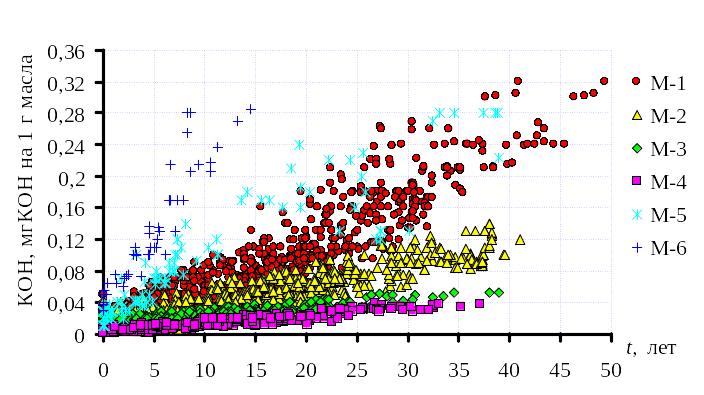
б

а – массив исходных данных;

б – этот же массив разбитый на группы с одинаковой скоростью окисления масел.

Рисунок 5.7 – Выделение групп трансформаторов с одинаковой скоростью окисления масел.