5.2 Диагностика по расстоянию в пространстве признаков

5.2.1. Диагностика по расстоянию до эталона.

В методе эталонов отнесение предъявленного для распознавания объекта к одному из диагнозов (состояний) совершается по наименьшему расстоянию до эталона [5.1-5.3]. В качестве эталона для диагноза принимается типичный объект, имеющий диагноз (рис. 5.1).

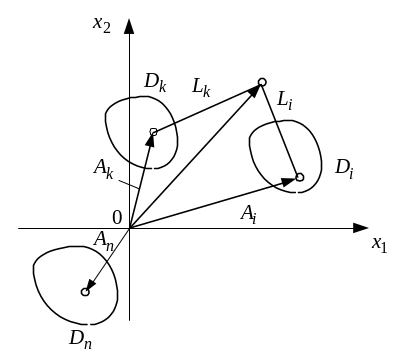
Рисунок 5.1 – Диагностика по расстоянию до эталона

Наиболее естественный выбор эталона состоит в использовании средних значений параметров в области диагноза. Если известны объектов с диагнозом , то в качестве эталона диагноза можно принять

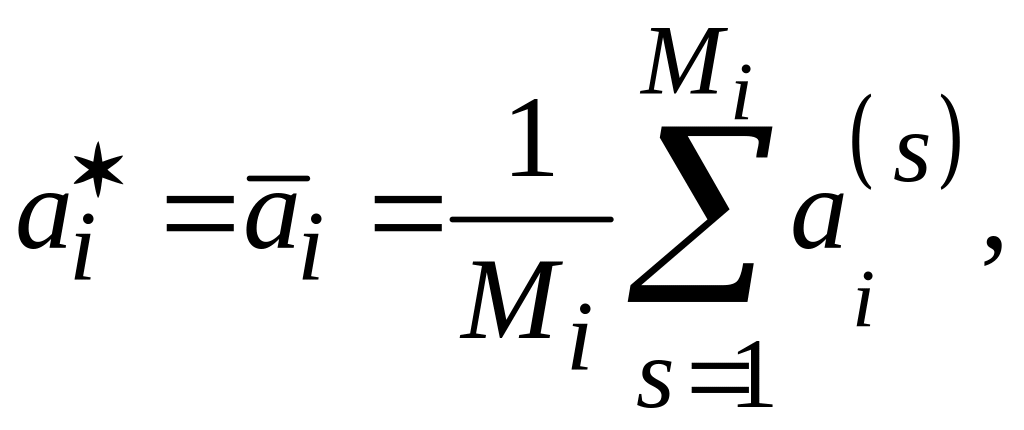(5.13)

где – объект с диагнозом (состоянием) (объект с верифицированным диагнозом).

Равенство (5.13) определяет эталон как центр тяжести области диагноза. Координаты вектора равны средним значениям координат векторов.

Алгоритм распознавания.

Допустим, что в пространстве признаков используется диагностическая мера расстояния L до эталонных точек . Объект относят к диагнозу , если мера расстояния между точками минимальна [5.1-5.3]:

если

или в другой форме

, если

В некоторых случаях условие принимается в более строгой форме где – порог распознавания (ε >0).

Надежность распознавания.

Очевидно, что надежность распознавания будет тем выше, чем меньше расстояние по сравнению с другими расстояниями. Это можно охарактеризовать коэффициентом распознавания

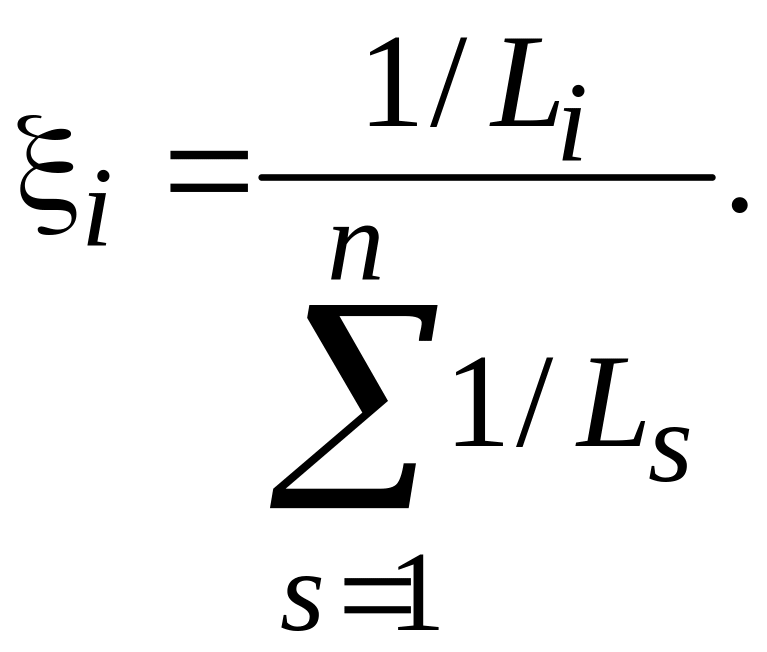(5.14)

Величина играет роль, сходную с вероятностью диагноза так как

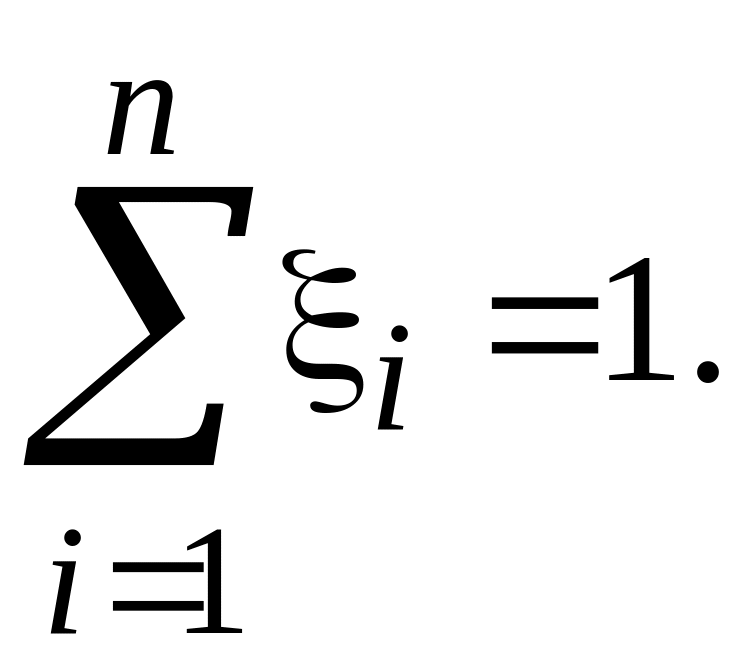(5.15)

Распознавание признается надежным, если , и где – заранее выбранный уровень распознавания.

При диагностике с порогами распознавания характерным является коэффициент помех

(5.16)

где – диагональ граничной области .

Например, при квадратичной мере расстояния

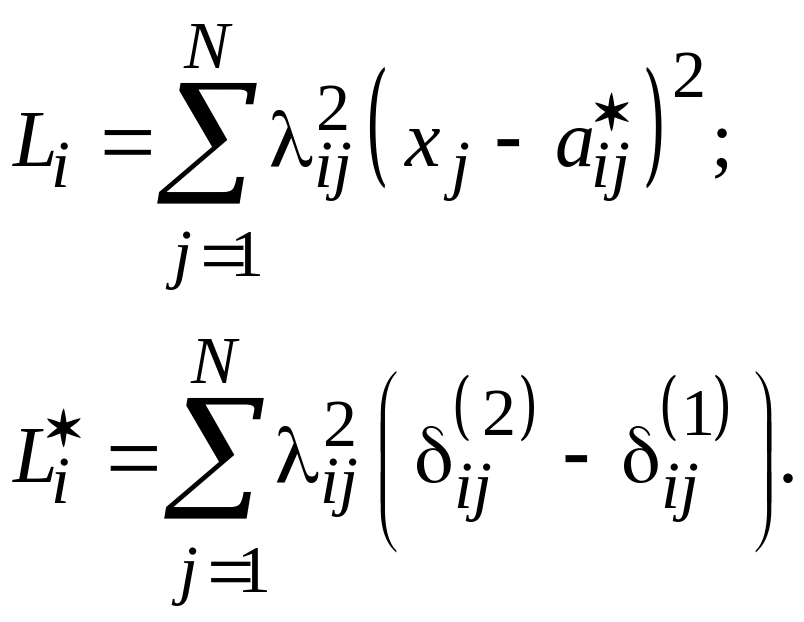
Чем больше коэффициент помех, тем ближе к предельной, граничной области располагается объект, предъявленный для распознавания.

5.2.2. Диагностика по угловому расстоянию

Близость вектора к эталонному вектору можно охарактеризовать с помощью угла между векторами [5.1]. Более удобно ввести в рассмотрение косинус угла между векторами, определяя его с помощью скалярного произведения

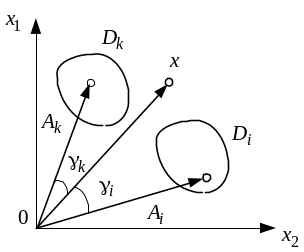
Рисунок 5.2 – Диагностика по угловому расстоянию

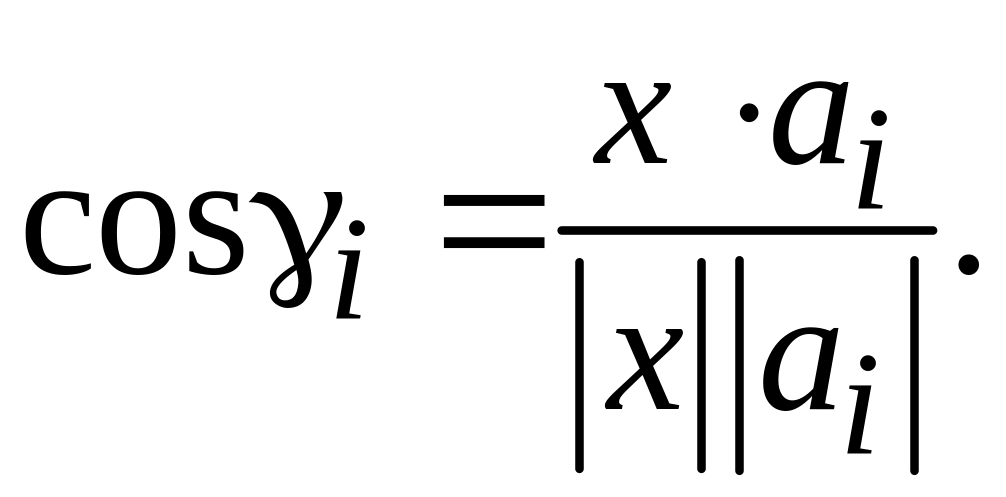(5.17)

Как видно из равенства (5.17), преобразования масштаба не влияют на угол между векторами. Скалярное произведение и норма векторов определяются также, как в обычном евклидовом пространстве:

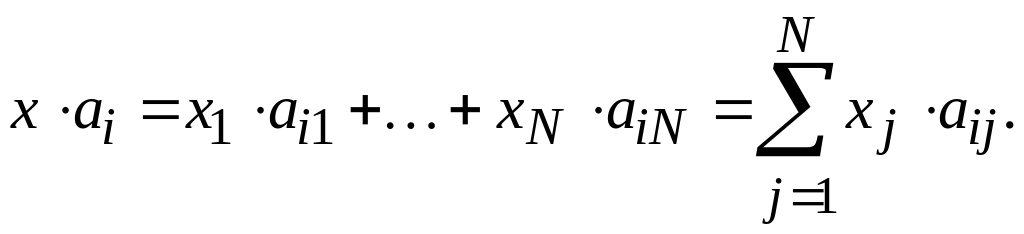
Если векторы и ортогональны, то

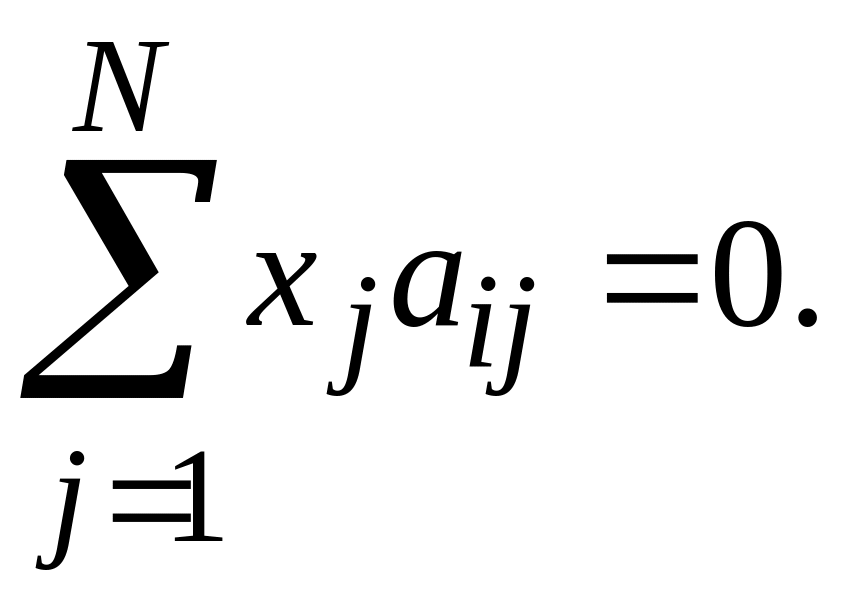
При диагностике по угловому расстоянию принимается решение , если угол между векторами и наименьший или .

5.2.3. Диагностика по расстоянию до множества.

В этом методе оценивается расстояние не от одной точки – эталона, а расстояния от точки (объекта, предъявленного для распознавания) до всех точек множества с данным диагнозом [5.1-5.3]. Расстояние до множества оценивается как среднее расстояние, но возможны и другие способы этой оценки. Использование рассматриваемого метода предполагает, что для каждого диагноза имеется группа образцов (объектов) с установленным диагнозом.

Пусть для диагноза D_i группа содержит M_i, образцов. Допустим, что выбрана диагностическая мера расстояния, и тогда расстояние от точки до точки (рис. 5.3), входящей в группу верифицированных образцов (при квадратичной мере),

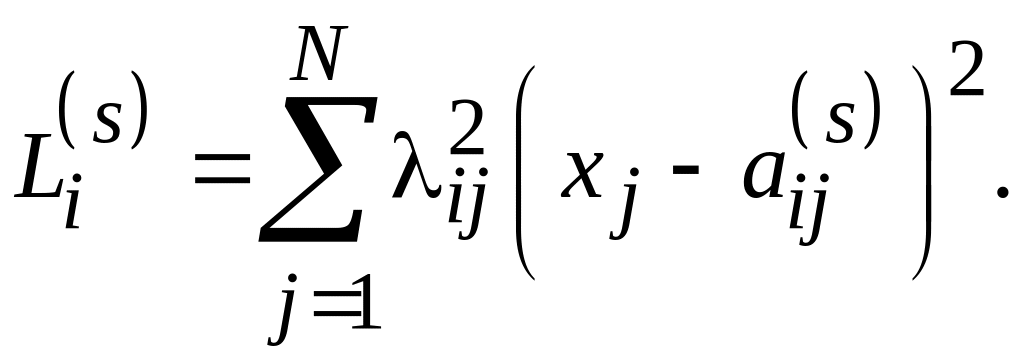(5.18)

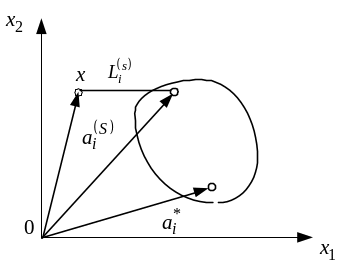
Рисунок 5.3 – Определение расстояния до множества

Можно определить среднее расстояние от точки до точек обучающей последовательности, принадлежащей диагнозу D_i:

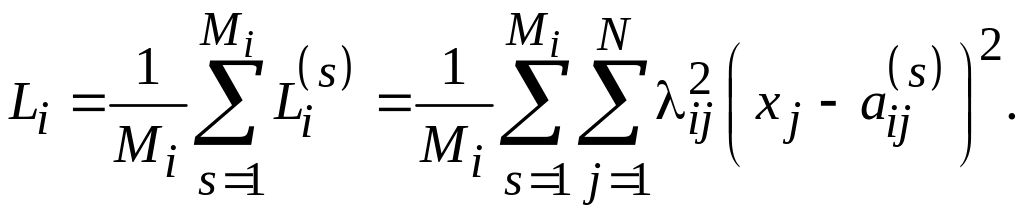(5.19)

При использовании обобщенной диагностической меры расстояния

(5.20)