5 Метрические методы распознавания

5.1 Метрика пространства признаков

Координаты пространства. В пространстве признаков объект характеризуется N-мерным вектором . Координаты пространства x_j могут быть непрерывными или дискретными величинами [5.1]. В последнем случае x_j представляет признак k_j, имеющий несколько диагностических разрядов. Часто используется кодирование признаков в бинарном коде. Тогда координата x_j выражается двоичным числом и может иметь значения: x_j1 = 0, x_j2 = 1. При использовании унитарного (двоичного) кода возможные значения таковых: x_j1 = –1, x_j2 = 1.

В диагностическом пространстве объект описывается вектором, размерность которого может отличаться от размерности вектора в пространстве признаков. В качестве координат диагностического пространства принимаются функции

Евклидово расстояние между точками.

Обычное расстояние между точками и пространства признаков

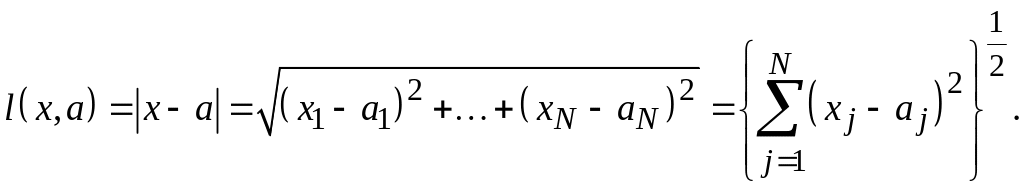(5.1)

Равенство (5.1) устанавливает, метрику евклидова пространства, причем основные метрические свойства этого пространства выражаются условиями:

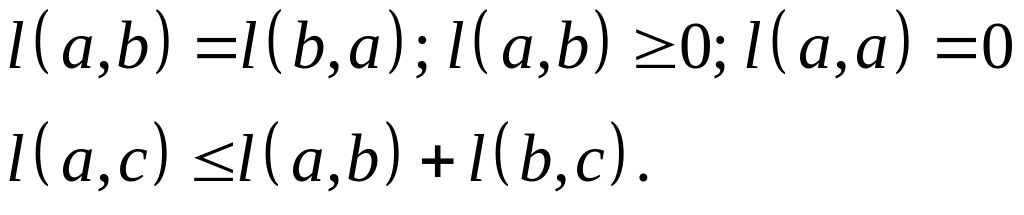(5.2)

В задачах распознавания удобно в качестве меры расстояния принимать квадрат расстояния

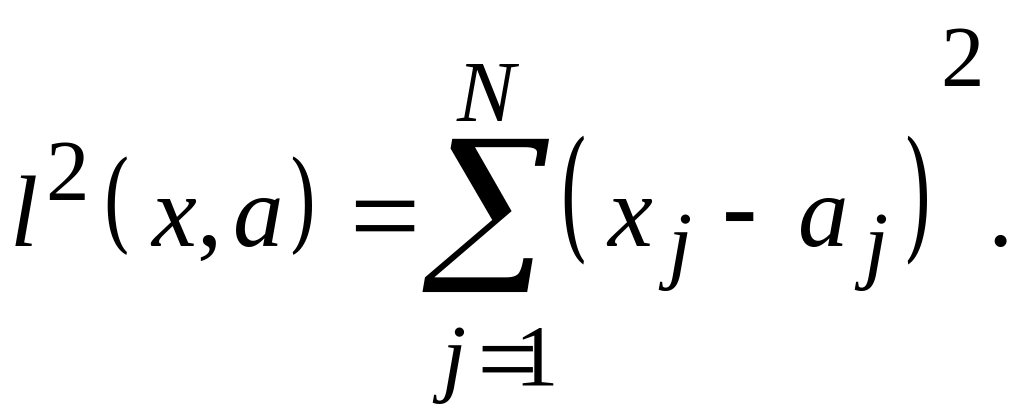(5.3)

Величина тесно связана с многомерным нормальным распределением, а неравенство

(5.4)

влечет за собой более сильное неравенство

(5.5)

Обобщенное расстояние порядка

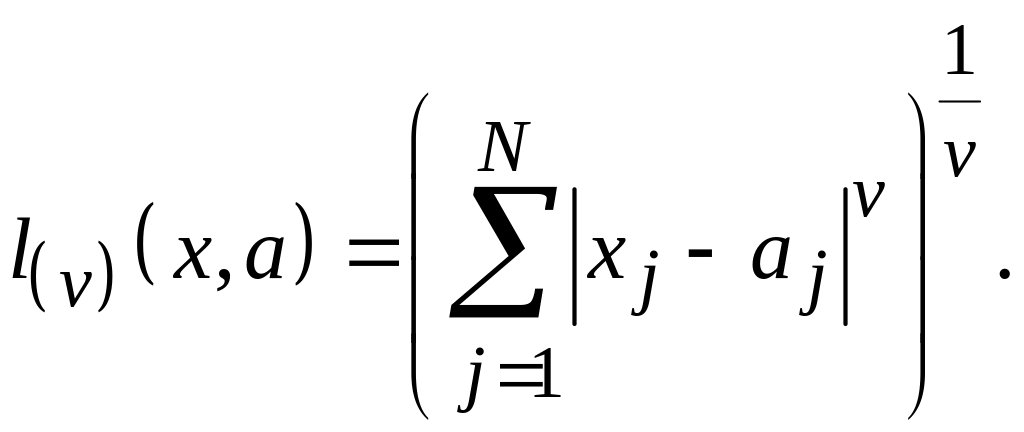(5.6)

При совпадает с обычным расстоянием, при величина представляет собой расстояние по Хеммингу. При 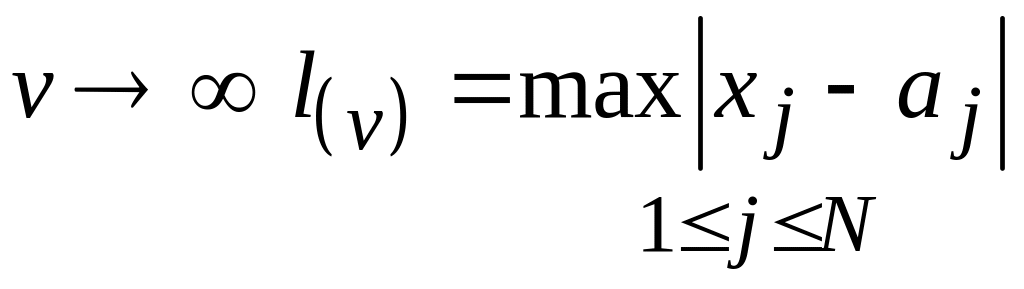, т.е. расстояние равно наибольшему отклонению по какой-либо из координат.

Метрика в неизотропном пространстве признаков.

Предыдущие определения расстояния соответствовали однородному, изотропному пространству признаков [5.1-5.3], координаты которого имеют общую единицу измерений. Такое пространство однородных признаков используется в ряде задач распознавания. Например, для акустической диагностики в качестве признаков могут применяться амплитуды соответствующих гармоник и т. п.

Диагностика с помощью признаков в двоичном коде соответствует использованию изотропного, однородного пространства признаков. Однако во многих задачах диагностики пространство признаков является анизотропным, т. е. единицы измерения в различных направлениях различны. Координатам могут соответствовать параметры различной физической природы (например, – температура, – давление и т. п.).

Если ввести весовые коэффициенты по координате , то квадрат расстояния между точками х и а

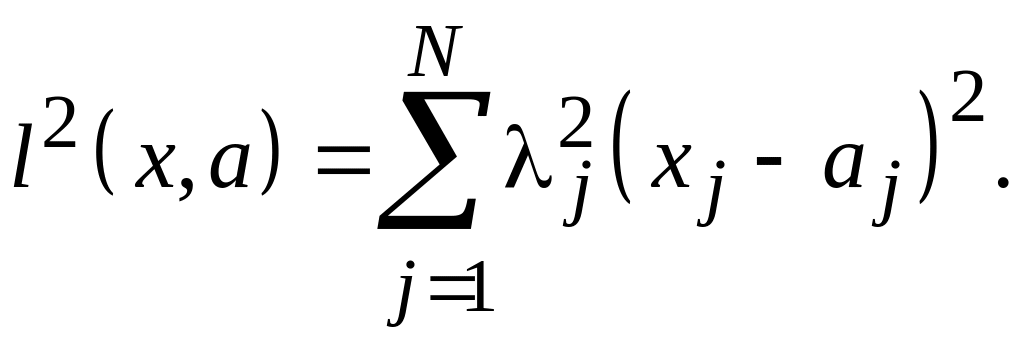(5.7)

С помощью компонентов весового вектора можно учесть различную диагностическую ценность признаков, придавая большее значение наиболее значимым признакам. Так как для диагностики важен относительный вес, то можно использовать условие нормирования в виде

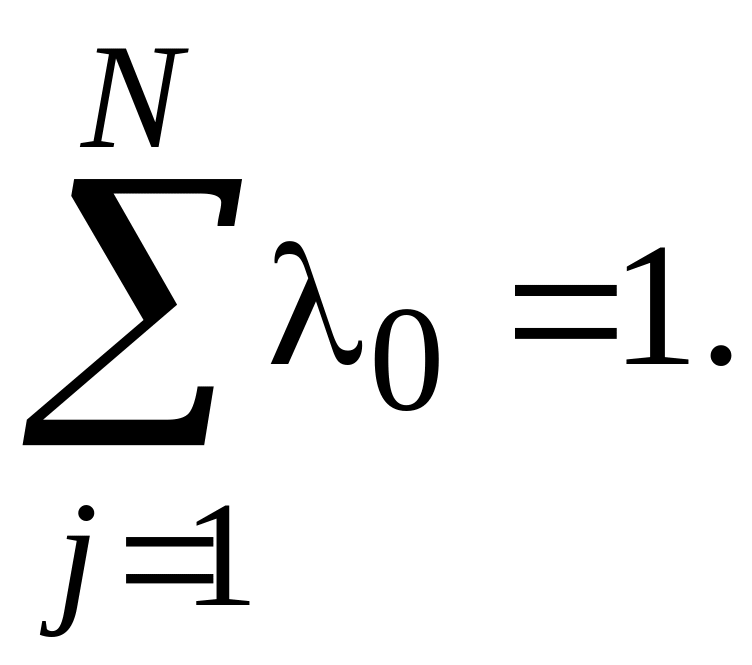(5.8)

Введение весовых коэффициентов деформирует пространство признаков. Если поставить условие, чтобы при подобных деформациях сохранился объем областей диагнозов, то условие нормирования можно принять таким:

.

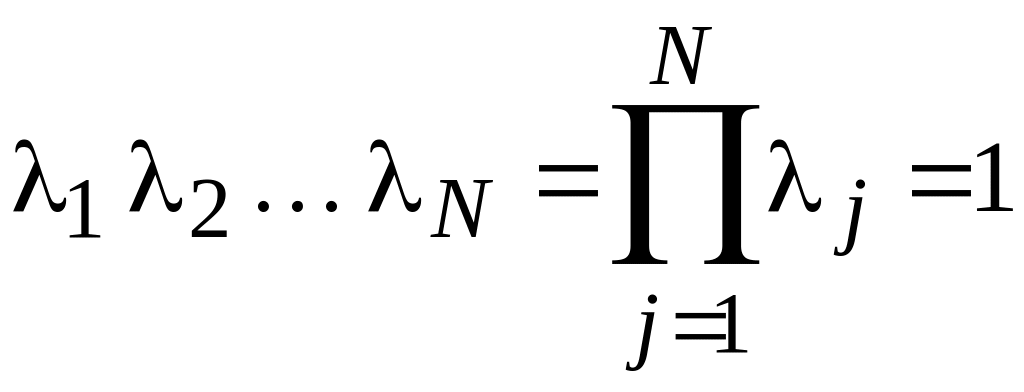Обобщенная метрика пространства признаков.

Соотношение (5.7) устанавливает «неравноправие» отдельных координат в пространстве признаков, но оно не учитывает роль координаты для диагноза . Диагностическое значение признаков различно для различных диагнозов и расстояние точки до точки , принадлежащей диагнозу .

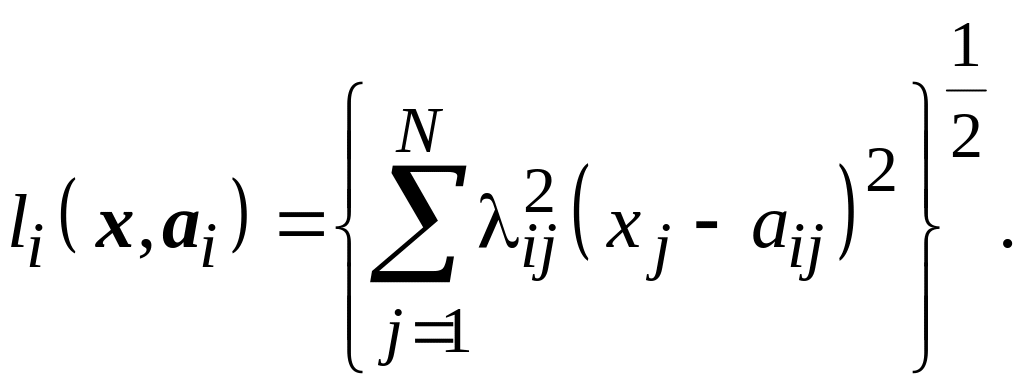(5.9)

Часто оказывается целесообразным принять

где – среднеквадратичное отклонение признака (параметра) для образцов с диагнозом .

Величина в этом случае имеет ясный физический смысл: чем меньше рассеяние признака по объектам, тем больше его диагностическое значение. В более общем случае можно положить

(5.10)

где безразмерный коэффициент характеризует диагностическую ценность признака.

Для дискретного параметра признака , имеющего искретных значений можно принять

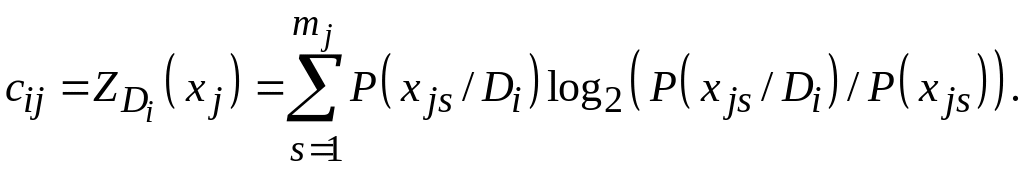(5.11)

Для непрерывно распределенных признаков вероятность дискретных значений заменяется плотностью вероятности, суммирование – интегрированием по области значений . В тех случаях, когда отсутствуют статистические сведения, величины могут быть назначены на основании экспертной оценки и т. п. В практических задачах величины подбирают с учетом опыта диагностики, причем принимают те значения, которые обеспечивают наибольшее число правильных ответов.

Условие нормирования при обобщенной метрике:

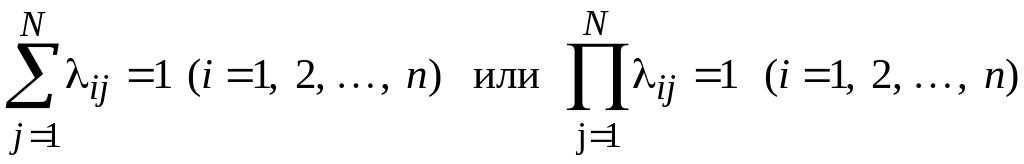(5.12)

Метрика, установленная равенством (5.9) изменяется не только для различных направлений, но и для различных диагнозов.

Замечание о классификации пространства признаков. В зависимости от используемой метрики, будем различать три вида пространства признаков.

Неизотропное, неоднородное пространство соответствует метрике общего вида (λ_ij ≠ 1). Если для всех диагнозов λ_ij = λ_i (i = 1, 2, …, n), то пространство называется однородным, неизотропным. Наконец, при λ_ij = λ_i = 1 (i = 1, 2, …, n; j = 1, 2, …, N) пространство считается однородным и изотропным.