6.4 Приклади застосування формули Стокса для знаходження циркуляції

Задача 1.

Обчислити циркуляцію вектора по кривій

Г:

Перше рівняння системи задає круговий циліндр радіуса 2, твірною якого є вісь Оz. Лінія Г являє собою окружність, що є перетином циліндра і площини перпендикулярноaї до осі циліндра (див. рис.8.).

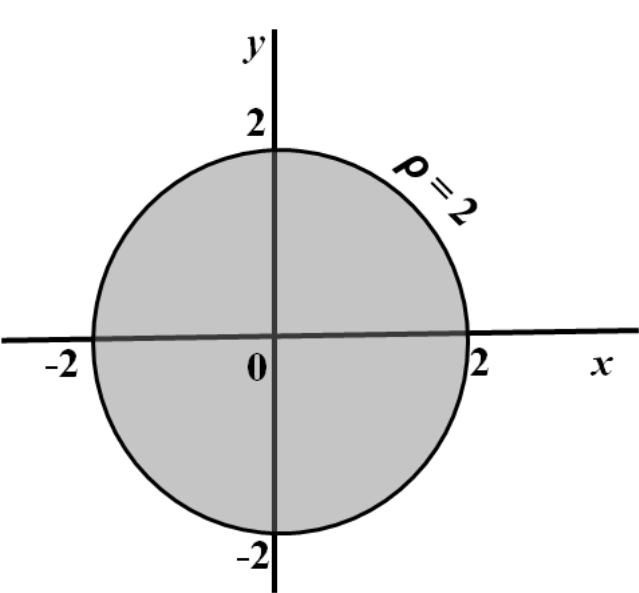
Рис.8. Схема до задачі 1.

Знайдемо ротор і нормаль:

rot , .

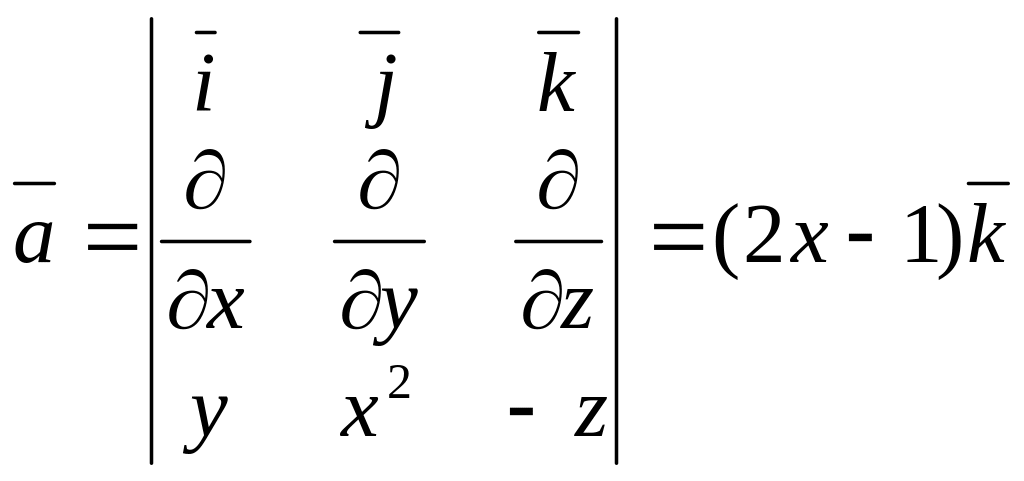Перевірка:

div rot

За формулою Стокса інтеграл по окружності перетворюється в інтеграл по колу

С= ,

де D проекція s в площину xOy (див. рис.8.). Для знаходження подвійного інтегралу по області Dперейдемо до полярних координат:

, , .

Рівняння окружності має вигляд =2, тому маємо:

Знайдемо внутрішній інтеграл:

Підставляючи цей результат у зовнішній інтеграл, отримуємо:

Знаходження подвійного інтеграла можна було спростити, якби розбити його на 2 доданки:

Перший інтеграл дорівнює 0, оскільки функція непарна по х, а область D симетрична щодо осі Оу (інтеграл по лівій частині скорочується з інтегралом по правій частині). Другий інтеграл дорівнює площі області інтегрування, тобто кола.

Задача 2.

Знайти циркуляцію вектора по границі області, обмеженої лініями

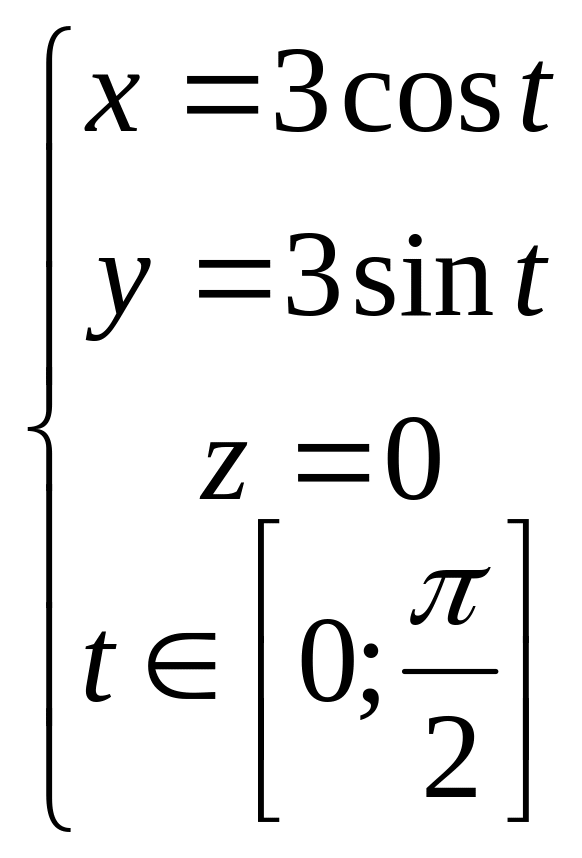х=0, y=0.

Контур інтегрування складається з дуги кола і двох відрізків (див. рис.9.).

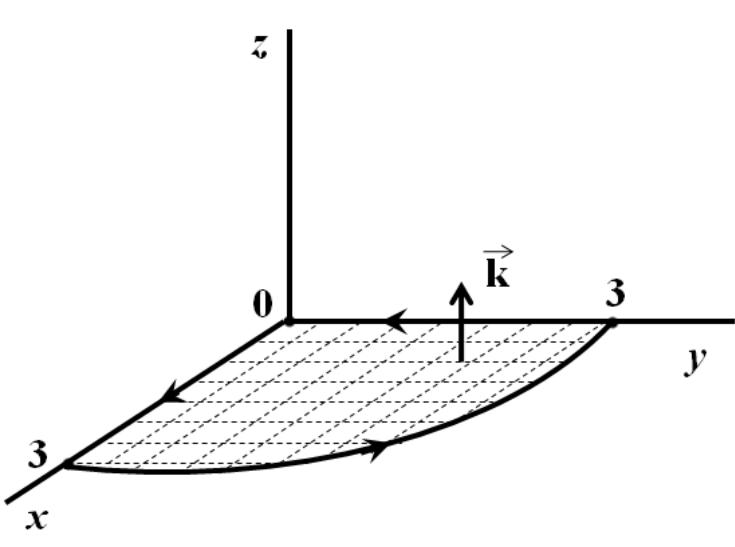
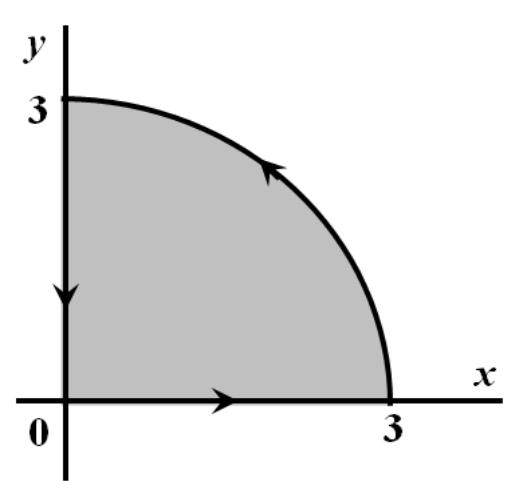
Рис.9. Схема до задачі 2.

Застосуємо формулу Стокса:

rot , ,

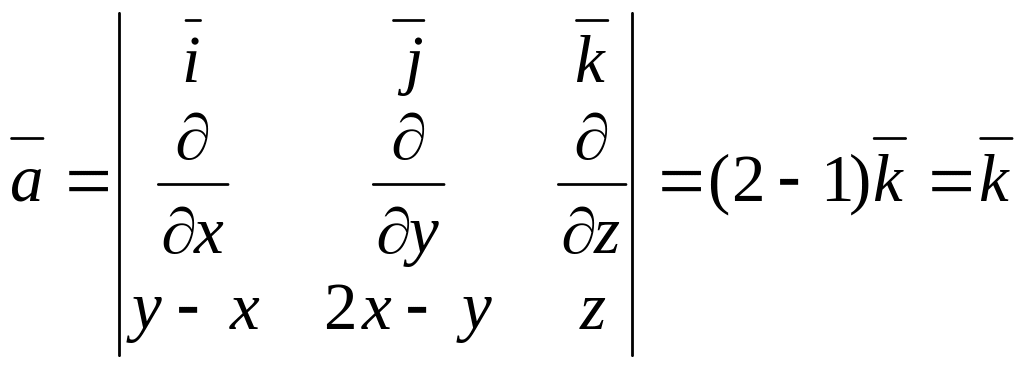Тут враховано, що інтеграл від одиниці дорівнює площі поверхні інтегрування, в даному випадку - чверті кола радіуса 3.

Задача 3.

Обчислити циркуляцію вектора

по контуру трикутника NPM: M(2;0;0), N(0;3;0), P(0;0;1).

Розв’язання:

Точки M, N I P лежать на координатних осях, відсікаючи на них відрізки, відповідно, 2, 3 і 1 (див. рис.10.).

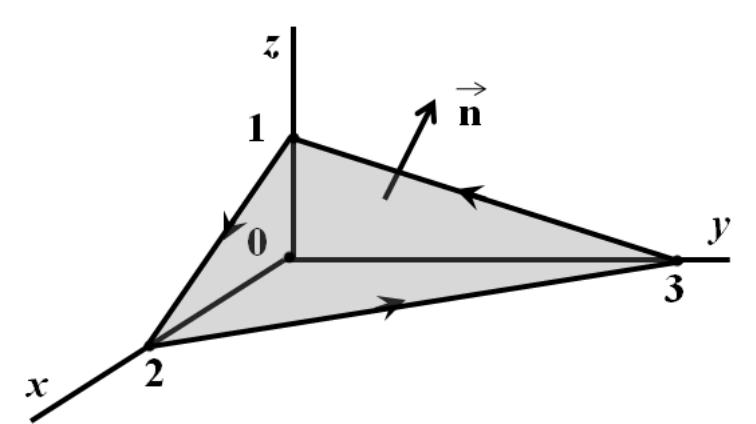
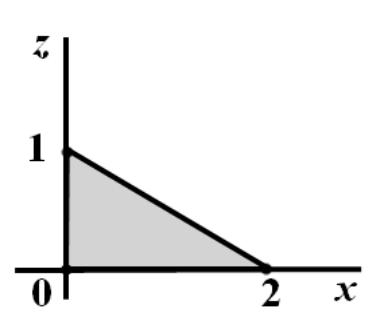
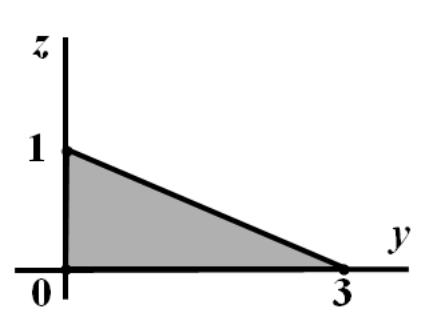
Рис.10. Схема до задачі 5.

Для запису рівняння площини MNP зручно використовувати рівняння площини у відрізках:

Домноживши обидві частини рівняння на 6, отримаємо:

3х+2у+6z-6=0.

Знайдемо ротор і застосуємо формулу Стокса:

Додатна нормаль створює гострі кути зі всіма координатними осями, зведемо поверхневий інтеграл другого роду до трьох подвійних:

Враховуючи властивості подвійного інтегралу, а саме, що інтеграл від одиниці дорівнює площі поверхні інтегрування, маємо, що подвійні інтеграли дорівнюють площам відповідних трикутників

.