6.3 Теоретичне значення формули Стокса

6.3.1 Інваріантне («фізичне») означення ротора

Ротор є одним з диференціальних операторів першого порядку. Формальне визначення ротора справляє враження деякої штучності цього оператору, залишається незрозумілим, чим принципово відрізняється ротор від інших можливих комбінацій частинних похідних першого порядку.

Серед усіх можливих операторів мати фізичний зміст, а значить і представляти інтерес, можуть тільки ті, які описують об'єктивні властивості, тобто ті властивості векторного поля, які не залежать від спостерігача, і, отже, не змінюються при переході до будь-якої іншої системи координат. При формальному визначенні ротора той факт, що він виявляється однаковим у будь-якій системі координат, є зовсім неочевидним. Формула Стокса дозволяє показати інваріантність ротора щодо вибору системи координат і виявити його фізичний зміст.

Нехай задана деяка точка простору М₀. Розглянемо деяку площину , що проходить через точку М₀. Нехай - одинична нормаль до цієї площини. Нехай D деяка область у площині , що містить точку М₀, а Г - границя області D. Розглянемо циркуляцію по контуру Г векторного поля , напрямок обходу і орієнтацію нормалі вважаємо узгодженими (див. рис.4.).

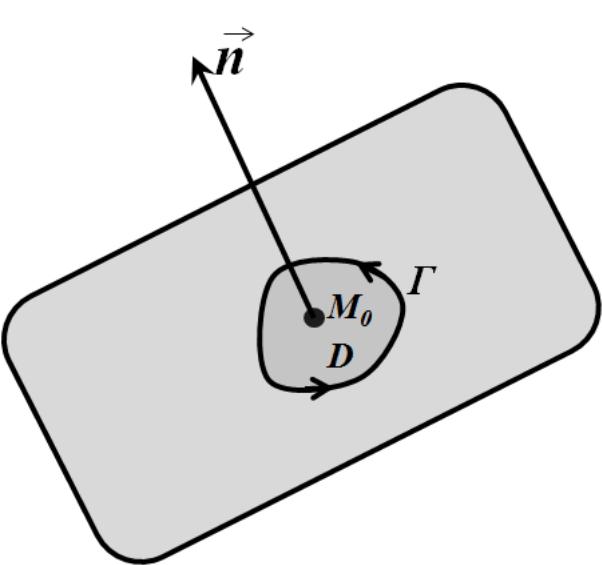
Рис.4. Фізичне значення ротора

За формулою Стокса маємо

.

Застосовуючи теорему про середнє, отримуємо

,

де М - деяка (взагалі кажучи, невідома) точка області D, а S_D позначає площу області D. Звідси отримуємо, що

.

Тепер почнемо «стягувати» контур Г в точку М₀, тобто будемо розглядати області все меншої площі, але обов'язково всі, що містять точку М₀. При

граничному переході діаметр області також буде прямувати до нуля, а значить

Отримаємо:

.

Ясно, що при необмеженому зменшенні розмірів області D довжина контура, а отже і циркуляція, прямують до нуля, тому під знаком границі ми маємо невизначеність виду . Сама границя означає інтенсивність обертальної компоненти векторного поля.

За визначенням скалярного добутку

,

Де - кут між нормаллю і вектором. Найбільшого значення скалярний добуток досягає, коли напрямок нормалі і ротора співпадають. В цьому випадку

.

Таким чином, абсолютна величина ротора відповідає максимальній (по всіх можливих напрямках) інтенсивності обертальної компоненти векторного поля, а напрямок ротора відповідає нормалі до площини, в якій обертальна компонента найбільша.

Останнє співвідношення можна взяти в якості визначення ротора. При такому визначенні незалежність ротора від вибору системи координат очевидна.

6.3.2 Наочний сенс ротора

Рух рідини або газу можна відстежувати спостерігаючи за переміщенням маленьких легких предметів, що знаходяться в потоці. Так, наприклад, характер течії річки можна вивчити, спостерігаючи як пливе по річці листя. При цьому неважко буде помітити, що багато листя не тільки пливуть за течією, але і повертаються, що викликано нерівномірністю течії.

Наочний образ ротора дає маленька легка кулька, яка закручується в потоці рідини або газу з неоднорідним полем швидкостей. Напрямок ротора відповідає осі обертання кульки, а модуль ротора пропорційній кутовій швидкості. Сказане можна проілюструвати простим, але важливим прикладом. Розглянемо плоский диск, що обертається навколо осі з деякою кутовою швидкістю . Нехай вісь обертання співпадає з віссю Оz. Кожна точка рухається по колу, її швидкість направлена по дотичній до окружності, тобто перпендикулярно радіус-вектору точки. Оскільки зв'язок між лінійню і кутовою швидкістю визначається формулою , величина швидкості буде пропорційна віддаленню точки від осі обертання,тобто довжині радіус-вектора (див. рис.5.).

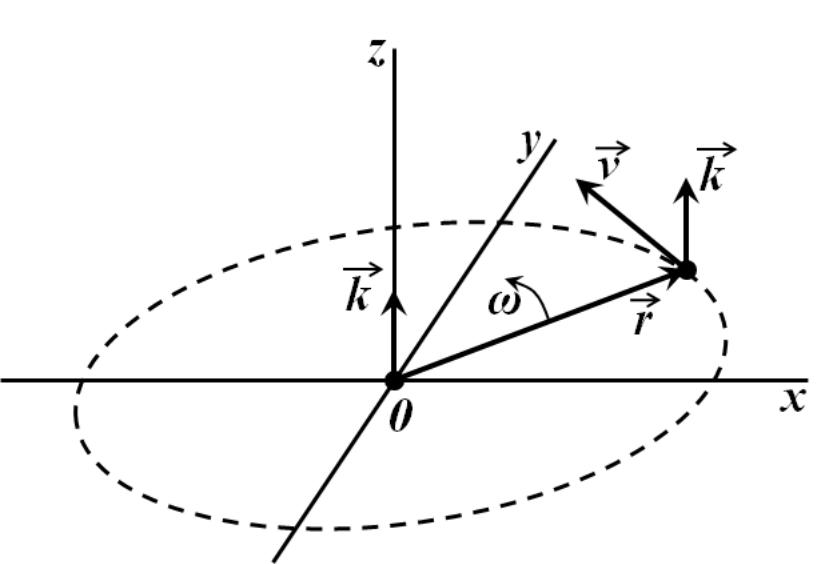
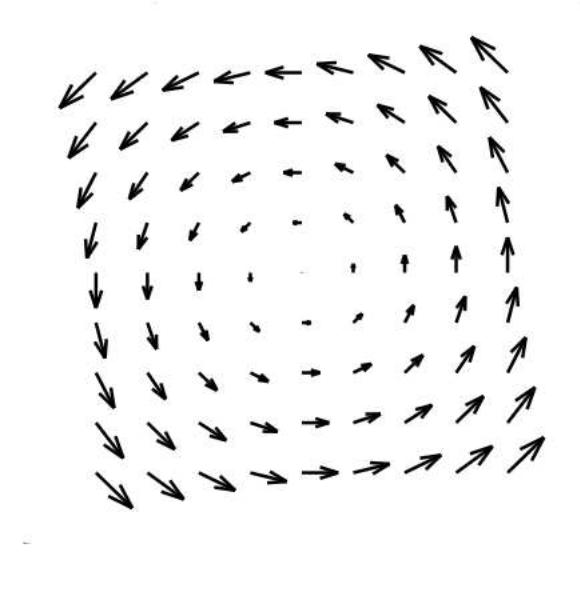
Рис.5. Поле швидкостей з постійним ротором

Оскільки вектор швидкості перпендикулярний осі орту осі Oz (вектору ) і радіус-вектору точки ( ), він лише числовим коефіцієнтом відрізняється від їх векторного добутку. Довжина векторного добутку дорівнює площі паралелограма, побудованого на векторах, в даному випадку площі прямокутника, тобто добутку довжин цих векторів:

, ,

де знак визначається орієнтацією трійки векторів , і . Неважко переконатися, що у випадку, коли обертання виконується проти годинникової стрілки, маємо:

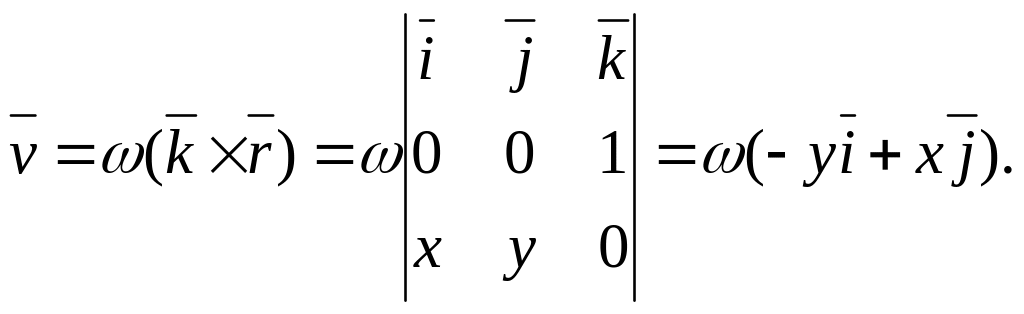
Знайдемо ротор вектора поля:

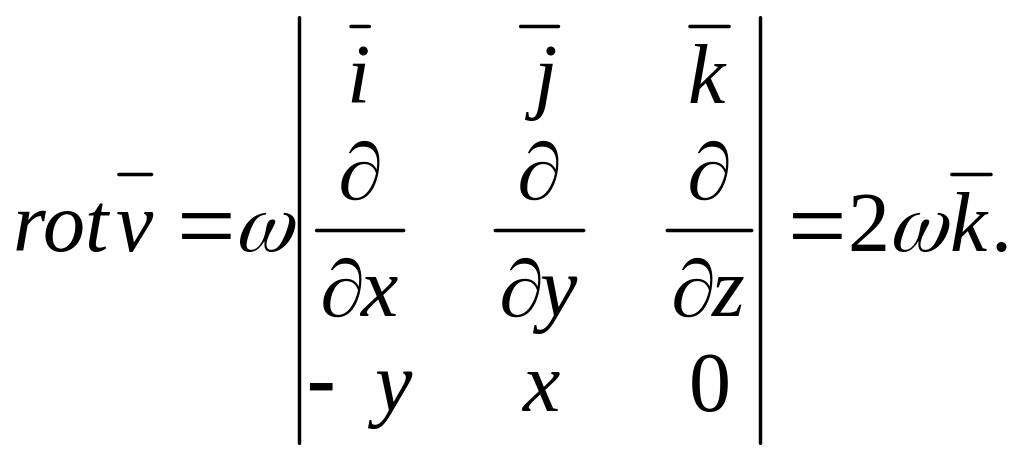
Таким чином, у всіх точках ротор є однаковим і дорівнює подвоєній кутовій швидкості. Напрямок ротора співпадає з віссю обертання. Якщо змінити напрямок обертання, то ротор поміняє напрямок на протилежний.

Розглянемо ще один простий приклад - неоднорідну одновимірну течія рідини. Нехай у всіх точках середовища напрямок швидкості збігається з напрямком осі Ох, а величина швидкості зростає пропорційно ординаті точки (див. рис.6.):

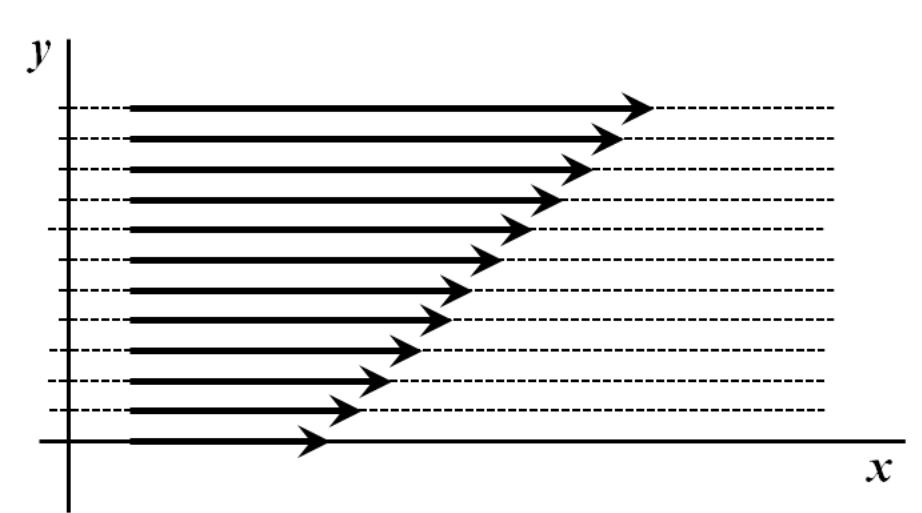
Рис.6. Неоднорідна одномірна течіям

.

Знайдемо ротор поля швидкостей:

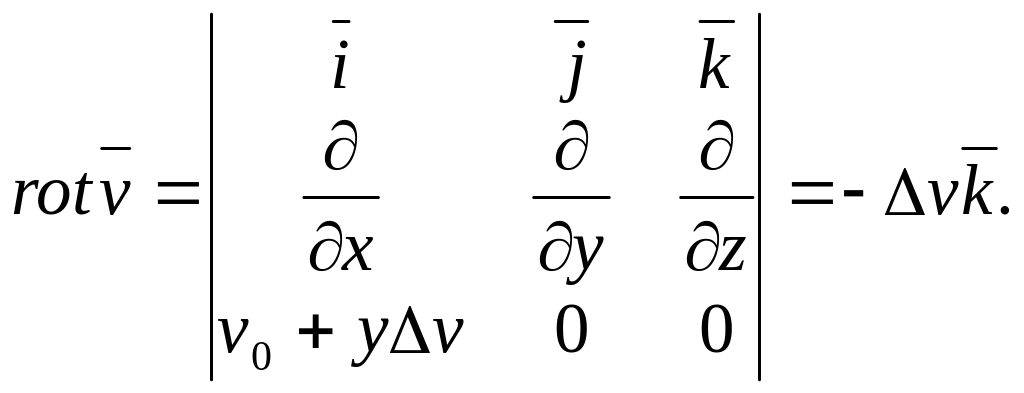
Ротор у всіх точках приймає однакове значення. Ротор спрямований перпендикулярно течії і перпендикулярно напрямку найбільшого перепаду швидкостей (градієнту). Напрямок ротора протилежний напряму осі Oz, що вказує на очевидний факт, що тіло, що потрапило в цей потік, буде закручуватися за годинниковою стрілкою, тобто в від’ємному напрямку.