6 Формула Стокса

6.1 Векторний і координатний запис формули Стокса

Нехай замкнена кусково-гладка крива Г являється межею кусково-гладкої поверхні S. Нехай поверхня S міститься в деякій трьохмірній області G R³, у всіх точках якої визначені і неперервні функції трьох змінних P, Q, R, а також їх частинні похідні. Тоді криволінійний інтеграл другого роду по кривій Г пов’язаний з поверхневим інтегралом другого роду по поверхні S формулою Стокса:

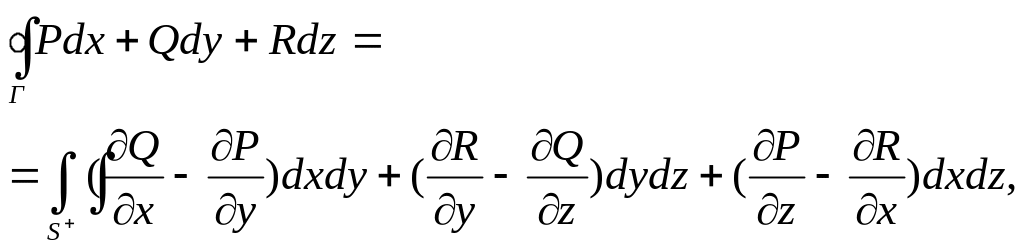
при чому напрямок контуру Г (в криволінійному інтегралі) і вибір додатного напрямку нормалі (в поверхневому інтегралі) узгоджені за «правилом буравчика» - додатною рахується та сторона поверхні, на якій додатній напрямок контуру відповідає руху проти часової стрілки (див мал.1).

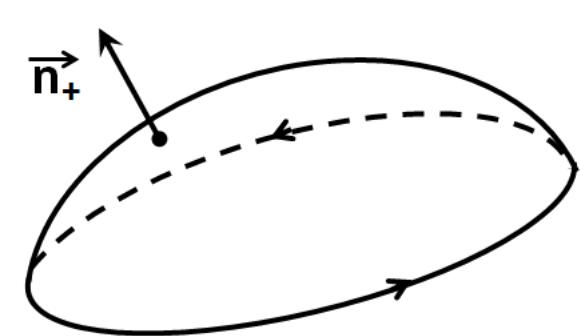
Рис.1. Узгодження орієнтації в формулі Стокса

Не важко побачити, що у випадку, коли крива Г лежить в площині xOy, формула Стокса переходить в відому формулу Гріна, яка зв’язує криволінійний інтеграл першого роду по плоскій кривій з подвійним інтегралом по області, обмеженій даною кривою (див. рис.2).

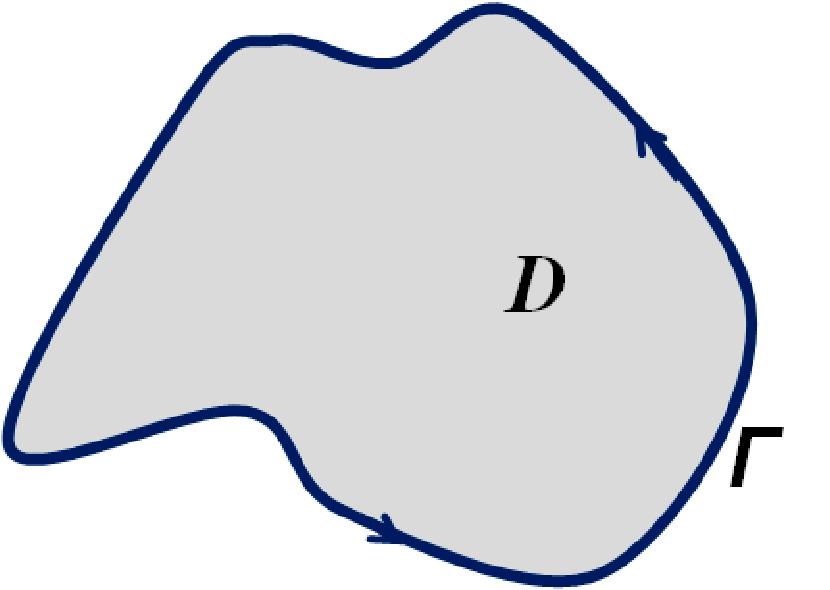
Рис.2. Обхід границі області в формулі Гріна

Загальний випадок формули Стокса формально виходить з формули Гріна циклічною перестановкою координат:

x→y→z→x, P→Q→R→P

Нехай - одиничний вектор зовнішньої нормалі до поверхні S. Тоді

де і - кути, які утворює цей вектор з координатними осями (косинуси цих кутів називають «направляючими косинусами»).

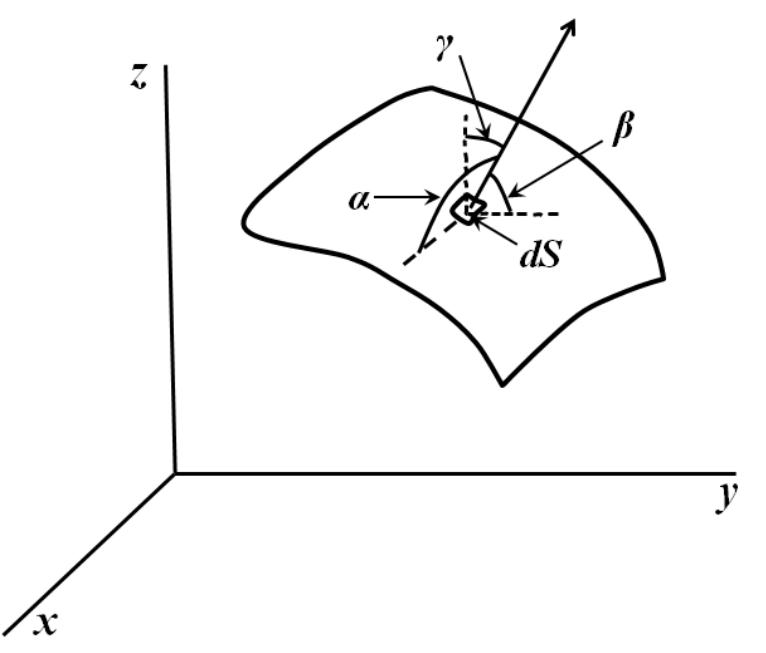
Рис.3. Направляючі косинуси нормалі

Оскільки зв'язок між поверхневими інтегралами першого і другого роду задається формулою

,

Формулу Стокса можна переписати у вигляді (рис.3.):

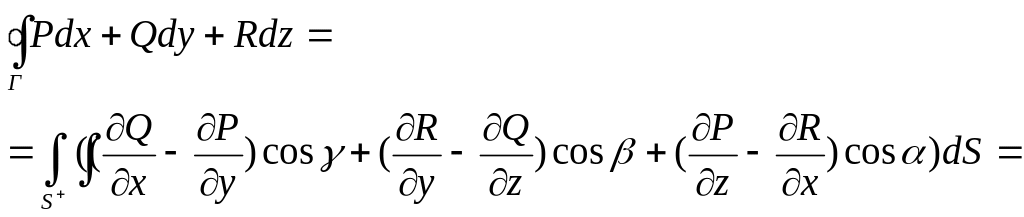
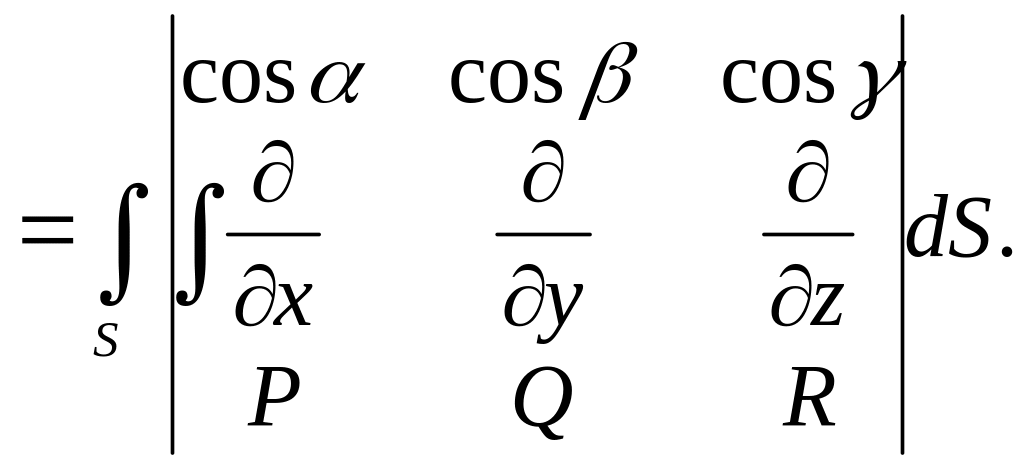
При знаходженні визначника третього порядку під «множенням» знака диференціювання (наприклад, ) на функцію підрозумовується знаходження відповідної частинної похідної.

Розглянемо вектор , координатами якого є величини P, Q, і R:

.

Не важко побачити, що під знаком поверхневого інтеграла першого роду стоїть скалярний добуток вектора на вектор

,

який називається ротором вектора (позначається rot ). Якщо ввести формальний вектор «набла» рівністю

,

то ротор можна формально представити, як векторний добуток вектора «набла» на вектор F:

.

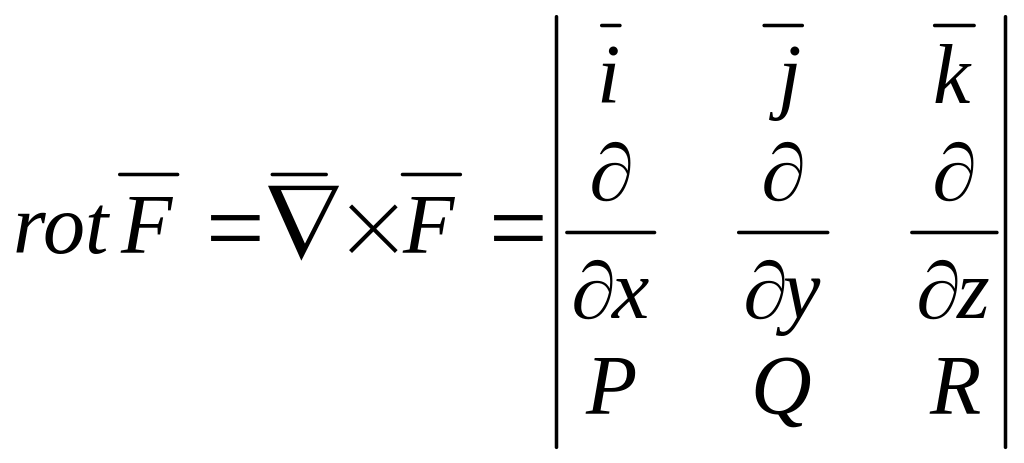Позначимо радіус-вектор довільної точки простору . Відомо, що координати радіус-вектора є координатами точки, на яку він вказує:

.

Введемо вектор елементарного переміщення

,

тоді формулу Стокса можна записати у векторній формі:

Криволінійний інтеграл по замкнутому контуру називається циркуляцією векторного поля, поверхневий інтеграл другого роду означає потік через поверхню. Отже, формула Стокса, допускає наступне словесне формулювання:

циркуляція векторного поля по замкнутому контуру дорівнює потоку його ротора через поверхню, що стягується цим контуром.

6.2 Коротка історична довідка

Розглянута формула пов'язується з ім'ям англійського фізика і математика ірландського походження Джорджа Габріеля Стокса (Sir George Gabriel Stokes).

Стокс народився в ірландському селі Скрін 13 серпня 1819. У 1841 році він закінчує Пемброкский коледж Кембріджського університету.

У 1849 році він займає посаду професора Кембріджського університету, і зберігає цю посаду до самої смерті 1 лютого 1903. «Люкассовску» кафедру, яку очолював Стокс, у свій час займав Ісаак Ньютон. Поряд з Максвеллом і Кельвіном Стокс стає одним з найбільш прославлених професорів Кембріджського університету.

Найбільш значущими є роботи Стокса в області математичного аналізу і математичної фізики, гідроаеродинаміки і оптики. Ім'я Стокса носить закон, що виражає силу тертя («лобового опору») сферичного тіла в потоці в'язкої рідини, на честь Стокса названа одиниця в'язкості в системі СГС. Стоксом було описано явище флуоресценції, і встановлена ​​залежність її спектра від спектра збудливого світла (правило Стокса). Його ім'я носять також «число Стокса» і функція потоку Стокса (гідродинаміка), радіус Стокса (біохімія), лінії Стокса і зсув Стокса (оптика), параметри Стокса і вектор Стокса (кількісне вираження поляризації електромагнітних хвиль).

Величезне значення в наш час мають розроблені Стоксом і Нав'є рівняння руху в'язкої рідини (рівняння Нав'є-Стокса). Ці рівняння використовуються в численних технічних розрахунках (рух рідин по трубах, дизайн автомобілів і літаків), а також при вивченні і моделюванні природних явищ (океанічних течій, течій в магмі Землі, поведінки плазми і міжзоряного газу, протікання крові в кровоносних судинах і т. д.). Рівняння Нав'є-Стокса лежать в основі розрахунку переміщення повітряних мас в атмосфері Землі для складання прогнозу погоди.

Заслуги Стокса були оцінені ще за життя. З 1885 по 1890 він був президентом Лондонського королівського товариства (The Royal Society of London for Improving Natural Knowledge). У 1852 році Стокс отримав медаль Рамфорда від Королівського Товариства, а в 1893 медаль Коплі. У 1889 роі Стокс за наукові досягнення отримав дворянський титул баронета, в 1887-1892 рр.. був членом парламенту від університету. Він був членом багатьох іноземних академій, в тому числі військово-медичної академії в Петербурзі. Іменем Стокса названо по одному кратеру на Місяці і на Марсі, мінерал стокезіт.

Цікаво відзначити, що будучи молодшим сином протестантського священика, Стокс зберігав релігійні переконання і консервативні погляди на протязі всього життя. У 1886 році він стає президентом Вікторіанського Інституту (Victorian Insitute), заснованого у відповідь на поширення еволюційного вчення. Він також був віце-президентом Британського і Закордонного Біблійного товариства (British and Foreign Bible Society), в 1891 році удостоюється престижного богословського поста Джіффордовского професора в Единбурзі і видає том «Природної теології».

Формула Стокса була опублікована в 1854 році, причому в дещо незвичній формі, як екзаменаційної задачі на щорічних змаганнях у Кембриджі (Smith's Prize Exams), які є аналогом математичних олімпіад та проводяться з 1768 року до теперішнього часу (в 1998 року вони були перетворені в Smith-Knight Prize). Варто відзначити, що головний приз за 1854 дістався 23-річному англійському математику Едварду Рауту і його ровеснику Джеймсу Максвеллу - який в наслідок заклав основи електродинаміки (рівняння Максвелла). Загальний список, підготовлений Стоксом, включав 17 завдань, в восьмій з них пропонувалося знайти доведення формули Стокса. Деякі автори пишуть, що в числі завдань, вирішених Максвеллом, була і відома восьма завдача, але переконливих посилань при цьому не наводиться. Так чи інакше, але перше доведення формули Стокса було опубліковано тільки в 1861 році німецьким математиком Германом Ганкелем.

Деякі дослідники відзначають, що відома формула була повідомлена Стоксу Кельвіном в листі від 2 липня 1850 року, тому в деяких книгах використовують назву «формула Кельвіна-Стокса». Проте варіанти близькі до цієї формули зустрічалися в більш ранніх роботах Стокса та інших дослідників (Остроградський, Гаусс, Грін, Коші).

Під теоремою Стокса розуміють зазвичай більш загальне твердження про диференційовані многовиди, яке в якості окремих випадків включає в себе як саму формулу Стокса, так і ряд інших інтегральних формул (Ньютона-Лейбніца, Остроградського-Гаусса та ін.)