5. Приклади і правила дій

Зовнішні диференціальні форми порядку р задаються виразами виду

, де .

Додавання таких виразів проходить покоефіцієнтно: треба додати коефіцієнти з одинаковими індексами . Таким чином, якщо

то

Аналогічно виконується множення на дійсні числа. Крім того, всякий вираз виду

(R)

при являє собою нульову форму, і диференціальна форма рівна нулю тоді і тільки тоді, якщо вона являється лінійною комбінацією виразів такого виду. Тому наведену вище 2-форму можна записати у вигляді

Із наведених міркувань випливають слідуючі правила:

1. рівність 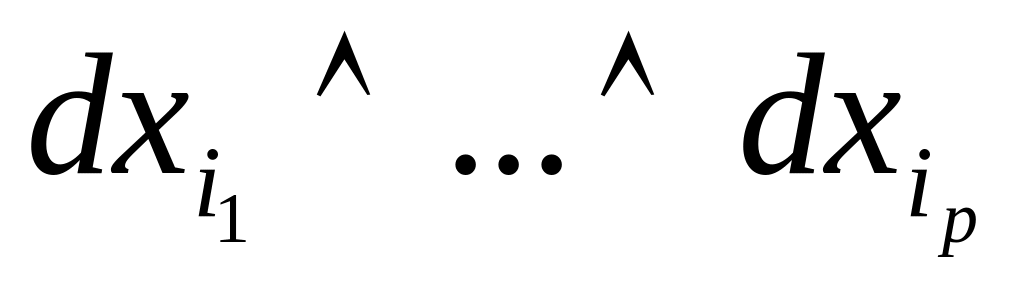має місце в тому і лише в тому випадку, якщо для деяких .

2. При р>n завжди =0.

3. , якщо всі індекси попарно різні і набір являється перестановкою набору .

При цьому а позначає число транспозицій, необхідних, щоб перевести набір в набір .

Щоб перемножити два «одночлена» і , необхідно записати їх один за одним и між ними поставити знак :

.

Зовнішній добуток довільних диференціальних форм вичисляється за дистрибутивним законом. Наприклад, в :

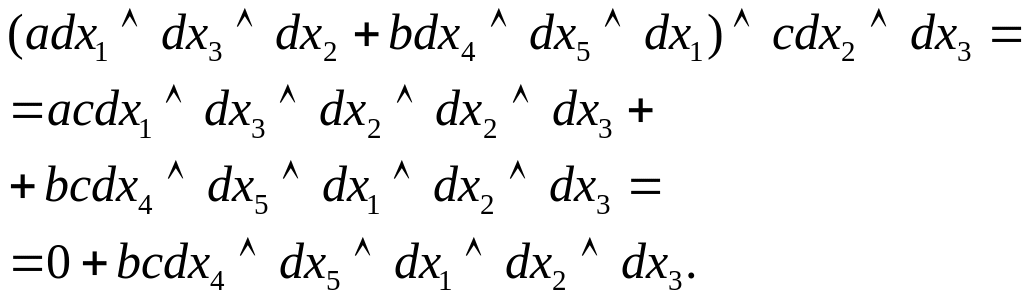
Порядок, в якому записані множники, є суттєвим.

Тепер дії над диференціальними формами можна виконувати, не посилаючись на визначення. Треба тільки враховувати вказані вище правила разом з їх наслідками (строго притримуючись правила, що вирази виду (R) рівні нулю).

Зараз ми хочемо навести приклади диференціальних форм в прострорах R₂ і R₃, причому нас будуть особливо цікавити умови, при яких форма, яку ми розглядаємо, є замкнутой або точною.

n=2, p=1. Нехай -диференційована 1-форма на площині. Вона є точною тільки в тому випадку, якщо існує така двічі диференційована функція , що

, .

На основі теореми 4.4 в цьому випадку форма повинна бути замкнутою: , тобто

Тому в якості необхідної умови точності форми ми отримуємо:

Це умова інтегрованості. Наведене тут доведення відрізняється від старого лише позначеннями.

Пфаффові форми в просторі R² давно застосовуються в термодинаміці. Проста термодинамічна система (наприклад, ідеальний газ) характеризується, скажемо, об’ємом V и температурою Т. Цій системі відповідають і деякі інші фізичні величини, одні з яких описуються функціями від V і Т, а інші — диференціальними формами: тиск р, внутрішня енергія Е, існування якої слідує з першого закону термодинаміки, і, крім того, дві диференціальні форми: нескінченно мала робота і нескінченно мала кількість тепла . В книгах по фізиці позначають символом , а - символом . Рівняння системи задають вид функцій р і Е:

І. р = р(V, Т).

II. Е = Е(V, Т).

Так як — точна форма, то

III.

Накінець, з другого закону термодинаміки випливає співвідношення

ІV. , так як є диференціал ентропії.

Написані вище чотири рівняння встановлені на основі фізичних роздумів. Вивчення наслідків, які можна з них вивести, природньо, являється задачою чисто математичною. В якості простого застосування правила ми покажемо, що між двума рівняннями стану системи виконується важливе співвідношення. Маємо

Відповідно,

V. .

Наприклад, у газу ван дер Ваальса, який підпорядковується рівнянню стану

де

енергія на основі рівняння V повинна залежати від об’єму.

Насправді, якби , то ми мали б . Але

Той факт, що , можна, наприклад, встановити за допомогою дослідження Джоуля-Томсона продавлюваня газу через пористу перегородку і, таким чином, проконтролювати справедливість розглядуваного рівняння стану.

n=2, p=1. Кожна диференційована 2-форма в К² являється замкнутою, так як її зовнішній диференціал, будучи 3-формою, рівний нулю. Якщо форма точна, тобто , де , то для коефіцієнтів а і ми отримаємо диференціальне рівняння з частинними похідними

.

n=3, р = 1. Пфаффова форма в R³

являється точною в тому і лише в тому випадку, якщо існує двічі диференційована функція f, у якої . Наприклад, для форми

,

де , і М – постійні і маємо

, де .

Форма (при правильному виборі сталих) описує ньютонівську силу гравітації, а функція є гравітаційним потенціалом. Замість фізики пишуть K=-grad(-f), де K - векторне поле.

Для того щоб 1-форма могла бути точною (мовою фізики,— щоб векторне поле К було потенціальним), повинна виконуватися рівність . Ця умова приводить до слідуючих трьох рівнянь:

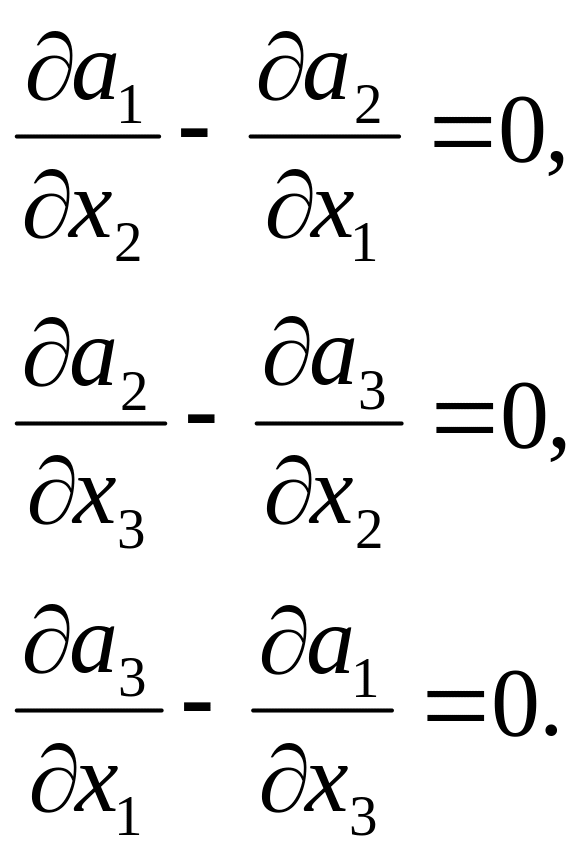
Якщо К знову позначає векторне поле , то в фізиці ці три рівняння записують у вигляді одного векторного . Ми бачимо тут і побачимо нижче, що у векторному аналізі використовуються занадто багато символів.

n=3, р = 1. Форма

є зовнішнім диференціалом пфаффових форм в тому випадку, коли

по-іншому кажучи, якщо a=rot b, де і . При цьому називається векторним потенціалом поля . Умова інтегрованості , тобто

в фізиці записують у вигляді div =0.

n=3, р = 1. Твердження, що для

і

приводить до рівняння з частинними похідними

Тобто div b = a.