
- •1. Грасманові добутки векторного простору
- •2. Зовнішні диференціальні форми
- •3.Диференційовані відображення
- •5. Приклади і правила дій
- •6 Формула Стокса
- •6.1 Векторний і координатний запис формули Стокса
- •6.2 Коротка історична довідка
- •6.3 Теоретичне значення формули Стокса
- •6.3.1 Інваріантне («фізичне») означення ротора
- •6.3.2 Наочний сенс ротора
- •6.3.3 Умова потенційності поля
- •6.3.4 Заключні зауваження
- •6.4 Приклади застосування формули Стокса для знаходження циркуляції
Вступ
В багатьох математичних і фізичних додатках теорії інтегрування недостатньо інтегрувати функції по всьому простору або по його вимірним підмножинам; необхідно знаходити інтеграли вздовж шляхів (криволінійні інтеграли) і по частинам поверхонь. Так, наприклад, щоб обрахувати роботу при русі точки в силовому полі, необхідно «просумувати силу вздовж лінії», тобто розглянути деякий криволінійний інтеграл вздовж пройденого цією точкою шляху. Подібним чином, кількість електроенергії, що протікає через криву поверхню, виражається поверхневим інтегралом і т. д. Спроба звести ці фізичні і аналогічні математичні питання в систему понять, якими можна було б легко оперувати, приводить до визначення поняття зовнішньої (або альтернованої) диференціальної форми. Об’єкти, які ми інтегруємо по р-вимірній частині поверхні в Rn, є диференціальними формами порядку р, а не функціями. Векторний аналіз з його бачаточисленними диференціальними операторами (grad f, rot a, div a) і інтегральними формулами є навряд чи доцільним, але часто дуже заплутаним перекладом обчислення зовнішніх диференціальних форм.
Отже, мета роботи: введення та опис поняття диференціальної форми, основних операцій над ними; показ доцільності використання диференціальних форм в задачах, що зводяться до обчислення інтегралів від функції багатьох змінних та обчислення параметрів векторних полів, ілюстрація переваги використання алгебри диференціальних форм перед методами векторного аналізу.
Завдання:
Описати основні об’єкти векторного аналізу
Описати алгебру диференціальних форм
Встановити зв’язок між ними
1. Грасманові добутки векторного простору
Літерою
Т ми
будемо
позначати деякий дійсний векторний
простір,
а символом Т* — простір,
спряжений
з Т,
тобто
векторний
простір
лінійних
форм в просторі
Т. Символом Тр
ми
будемо
позначати
р-кратний
декартовий
добуток
простору
Т на себе,
тобто
множину
всіх
р-наборів
![]() ,
елементів
простору
Т.
,
елементів
простору
Т.
Означення
1.1. Р-лінійною
формою
(де р![]() 1)
в просторі
Т називається
відображення
1)
в просторі
Т називається
відображення
![]() ,
,
що має сідуючі властивості:
для кожного
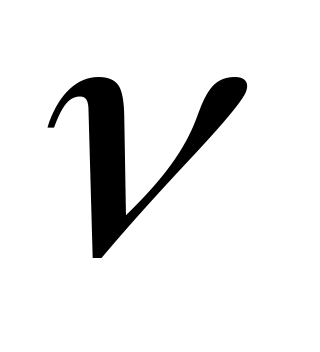 ,
що
задовольняє умову
,
що
задовольняє умову
 ,
,
![]()
при
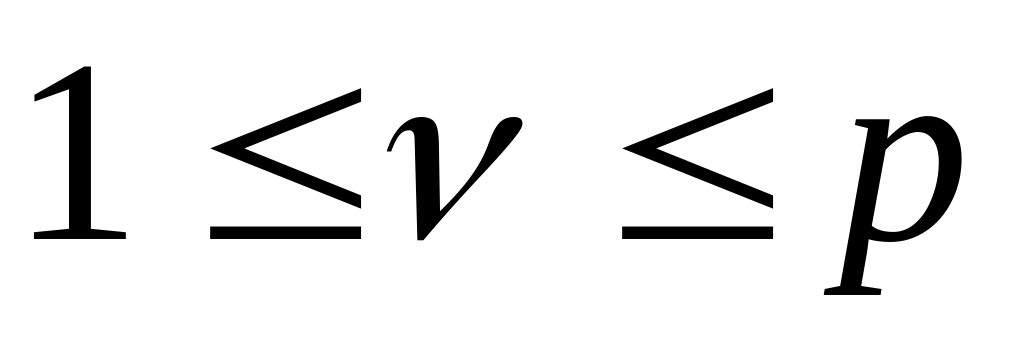 і
і

![]()
0-лінійною формою називається дійсне число.
Таким
чином,
р-лінійна
форма
![]() є
функція
від
р векторів,
лінійна
відносно
кожної
окремої
змінної;
1-лінійні
форми
просто являються
елементами
спряженого простору
Т*. Точно так , як
і
у
випадку
1-лінійних
форм, можна
показати,
що
р-лінійні
форми
створюють
дійсний
векторний
простір.
Число р називається
порядком форми
,
а
називається
полілінійною
формою
порядку
р.
є
функція
від
р векторів,
лінійна
відносно
кожної
окремої
змінної;
1-лінійні
форми
просто являються
елементами
спряженого простору
Т*. Точно так , як
і
у
випадку
1-лінійних
форм, можна
показати,
що
р-лінійні
форми
створюють
дійсний
векторний
простір.
Число р називається
порядком форми
,
а
називається
полілінійною
формою
порядку
р.
Іноді вимагаються більш загальні поняття:
Означення 1.2. (р, q)-лінійною формою в просторі Т (де р і q 1) називається відоброження
![]()
лінійне відносно кожної окремої змінної; р-форми в просторі Т називають також (р, 0)-лінійними формами, а q-форми в просторі Т* називаються (0, q)-лінійними формами в просторі Т.
Таким
чином,
при а,![]()
![]() і
і
![]() маємо
маємо
![]()
![]()
Векторний
простір,
створений
(р,q)-формами,
ми
будемо
позначати
символом![]() .
.
В подальшому нам будуть майже всюди зустрічатися р-форми.
Означення
1.3. р-лінійна
форма
називається
зовнішньою
р-формою,
якщо
для кожного
,
що
задовольняє умову
![]()
![]()
Кожна 1-лінійна форма (при р=1) є зовнішньою. Зовнішніми 0-формами ми за означенням вважаємо дійсні числа. Замість «зовнішня» часто говорять «альтернована» або «кососиметрична»; всі ці терміни означають одне і теж.
Теорема
1.1. Для кожного
р зовнішні
р-форми
створюють дійсний
векторний
простір
Ер,
що
називається
р-кратним
грасмановим
добутком
над простором
Т. При цьому
![]() і
і
![]() .
.
Насправді,
разом
з формами
![]() і
і
![]() і
форма
і
форма
![]() є зовнішньою;
якщо
є зовнішньою;
якщо
![]() і
і
![]() ,
то
,
то
![]() .
.
З означення випливає, що:
Якщо і
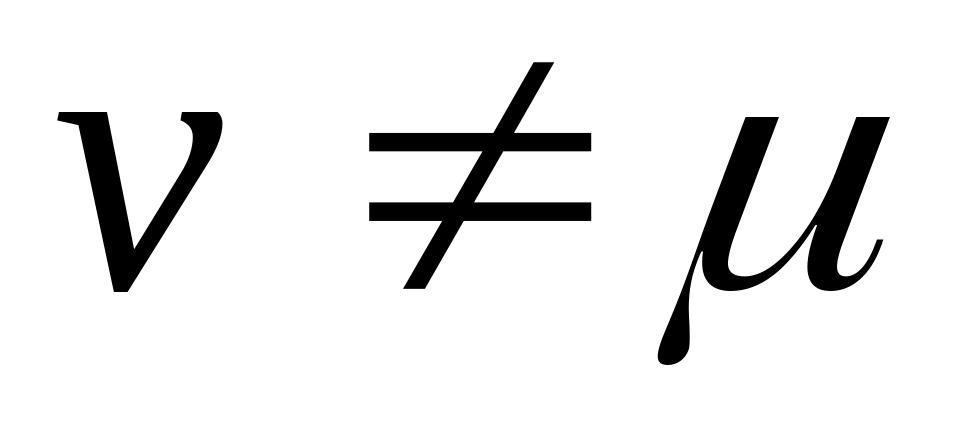 ,
то
,
то
![]()
Якщо
 при
,
то
при
,
то
![]()
Щоб встановити подальші властивості зовнішніх р-форм, ми введемо символ Кронекера.
Означення
1.4. Для будь-яких
двох
натуральних
чисел
![]() i
i
![]() покладемо:
покладемо:
![]()
Якщо![]() і
і
![]() —
який-небудь р-набір
натуральних
чисел, то покладемо
—
який-небудь р-набір
натуральних
чисел, то покладемо
![]()
Функція
![]() називається
символом Кронекера. Крім
того, для кожного
натурального числа і
покладемо
називається
символом Кронекера. Крім
того, для кожного
натурального числа і
покладемо
![]()
Таким
чином,
символ Кронекера
![]() приймає
тільки
значення
-1,
0 або
+1. Очевидно,
=
0 в тому
випадку,
якщо
два різних
аргумента, наприклад
приймає
тільки
значення
-1,
0 або
+1. Очевидно,
=
0 в тому
випадку,
якщо
два різних
аргумента, наприклад
![]() і
і
![]() при
,
співпадають.
Справедлива
така властивість
при
,
співпадають.
Справедлива
така властивість
Властивість
1.
![]()
З
цієї
властивості випливає
проста інтерпритація
символа Кронекера.
Тобто,
якщо
серед
чисел
![]() ,
які
ми
вважаємо
попарно різними,
будемо
створювати
транспозиції
до тих
пір,
поки
числа
не будуть
записаними
в природньому
порядку,
наприклад
,
які
ми
вважаємо
попарно різними,
будемо
створювати
транспозиції
до тих
пір,
поки
числа
не будуть
записаними
в природньому
порядку,
наприклад
![]() ,
то при кожній
окремій
транспозиції
знак символа
,
то при кожній
окремій
транспозиції
знак символа
![]() зміниться.
Якщо
а
— число всіх
проведених
транспозицій,
то
зміниться.
Якщо
а
— число всіх
проведених
транспозицій,
то
![]()
і,
значить,
оскільки
![]() 1,
1,
![]() .
.
Р-набором
(![]() )
визначається
не саме
число а,
але,
як
показує
це
припущення,
число
)
визначається
не саме
число а,
але,
як
показує
це
припущення,
число
![]() ,
тобто
«парність»
числа а.
,
тобто
«парність»
числа а.
Символ
Кронекера слугує
для
того, щоб
«альтернувати»
довільну р-лінійну
форму. Як
відомо,
множину
з
р
об’єктів
можна
упорядковувати
рівно
р! різними
способами. Таким чином,
кожному
р-набору векторів
![]() можна,
міняючи
місцями вектори
можна,
міняючи
місцями вектори
![]() ,
поставити
в відповідність
р! елементів
,
поставити
в відповідність
р! елементів
![]() .
Розуміється,
всі
ці
елементи
відрізняються
один від одного лише
в тому
випадку,
якщо
.
Розуміється,
всі
ці
елементи
відрізняються
один від одного лише
в тому
випадку,
якщо
![]() при
при
![]() .
.
Означення 1.5. Нехай — деяка р-лінійна форма. Під альтернованою частиною форми ми розуміємо р-лінійну форму [ ], що означається формулою
![]()
Якщо р=0, то ми покладаємо [ ]= .
Наприклад, при р=2
 де
де
![]() і
і
![]()
У випадку р=1, природньо [ ]= . Те, що форма [ ] є р-лінійною, легко перевіряється. Далі, має місце
Тведрження 2. Якщо — зовнішня р-форма, то =[ ].
Твердження 3. Форма [ ] являється кососиметричною.
Твердження 4. [[ ]] = [ ].
Має місце тривіальне твердження.
Твердження
5. Якщо
і
![]() — дві
р-лінійні
форми,
то
— дві
р-лінійні
форми,
то
![]() Для кожного
має
місце
рівність
Для кожного
має
місце
рівність
![]() .
.
Тепер ми визначимо добуток полілінійих форм. Нехай — деяка р-лінійна форма, а — деяка q-линейная форма. Покладемо
![]()
де
![]() і
і
![]() —
вектори
з Т. Ця
формула визначає
(р+q)-лінійне
відображення
—
вектори
з Т. Ця
формула визначає
(р+q)-лінійне
відображення
![]()
яке ми будемо називати добутком форм і . Відразу перевіряємо слідуючі правила:
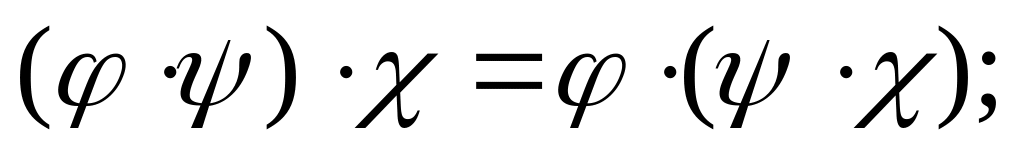


 де
.
де
.
Твердження
6.
![]() .
.
Означення 1.6 Нехай — зовнішня р-форма и — зовнішня q-форма. Зовнішнім добутком форм і називається форма
![]() .
.
Таким
чином,
![]() є
зовнішньою
(р+q)-формою.
Зовнішній
добуток
не є
добутком
в Ер,
бо
при р>0 добуток
двох
р-форм не лежить
в Ер.
Зовнішній
добуток
відображає
декартовий
добуток
є
зовнішньою
(р+q)-формою.
Зовнішній
добуток
не є
добутком
в Ер,
бо
при р>0 добуток
двох
р-форм не лежить
в Ер.
Зовнішній
добуток
відображає
декартовий
добуток
![]() в
просторі
в
просторі
![]() .
.
Теорема
1.2. а)
![]() де
де
![]() ,
,
![]() ;
;
б)
![]() де
де
![]() ,
,
![]() ;
;
в)
![]() де
де
![]() ,
,
![]()
![]() ;
;
г)
![]() де
,
,
.
де
,
,
.
Як видно вже з тривіальних прикладів, зовнішній добуток не комутативний. Що виникає при перестановці співмножників, найлегше всього вияснити, скориставшись базисом простору Т.
