6. Содержание отчета:

   1. Наименование работы.

   2. Цель работы.

   3. Графы сетей Петри по заданию с комментариями.

   4. Графы сетей Петри по заданию с указанием маркировки.

   5. Ответы на контрольные вопросы.

7. Контрольные вопросы:

   1. Что называется сетью Петри?

   2. Какие элементы входят в состав сети Петри?

   3. Что называется порождающей грамматикой?

   4. Как связаны входная и выходная функции сети Петри?

   5. Что управляет работой сети Петри?

Лабораторная работа 9 Исследование сетей Петри

1. Цель работы:

   1. Изучить метода исследования моделей сети Петри на основе построения дерева достижимых разметок.

   2. Проведение исследования сети Петри.

2. Литература:

   1. Молчанов А.Ю. Системное программное обеспечение. – СПб.: Питер, 2006. – 395с.

   2. Свердлов С.З. Языки программирования и методы трансляции. – СПб.: Питер, 2007. – 637с.

   3. Тонаненбаум Э. Компьютерные сети. – СПб.: Питер, 2008 – 991с.

   4. Сырецкий Г.А. Информатика. Фундаментальный курс. Том 1, 2. – Москва, 2005- 234с.

   5. Душин В.К. Теория основных информационных процессов и систем. – Москва, 2009 – 348 с.

   6. Русская компьютерная библиотека. URL: http://www.rusdoc.ru

3. Основное оборудование:

   1. ПЭВМ.

   2. Среда разработки Паскаль, С++, Delphi 7.

4. Задание:

   1. Изучить теоретический материал по теме «Способы реализации и применение сетей Петри».

   2. Выполнить задания.

   3. Составить отчет по работе.

5. Порядок выполнения работы:

   1. Запустить среду разработки.

   2. Выполнить следующие задания:

Теоретические сведения

Сеть Петри (СП) это двудольный, ориентированный мультиграф N = (Р, Т, F, Н, 0), где Р - конечное непустое множество элементов, называемых позициями; Т - конечное непустое множество элементов, называемых переходами; F:РхT→{0,1,2,...} и H:TxР→{0,1,2,...} функции инцидентности; 0 :Р→{0,1,2,...} - начальная разметка.

СП обычно представляют в виде геометрического объекта. При этом позиции изображаются кружками, переходы - черточками или прямоугольниками. Дуга проводится от позиции рi к переходу tj в том случае, если F(pi,tj)=>1, а от перехода tj к позиции рi если H(tj ,pi)>=1.

Если F(pi , tj)=> 1 , то позицию рi называют входной к переходу tj, а переход tj выходным к позиции pi. Множество входных позиций к переходу tj определяется выражением pre(tj)={p:F(p,tj)>=1}, а множество выходных переходов к позиции рi выражением post(pi)={t:F(pi,t)=>1}. Аналогично определяются множества входных переходов и выходных позиций.

При функционировании СП переходит от одной разметки к другой. Переход t может сработать при разметке , если ppre(t): (p)-F(p,t)>=0, где (p) число меток в позиции р. В результате срабатывания перехода t новая разметка ' возникает в соответствии со следующим правилом:

p (pre(t)Upost(t)): '(p)= (p)-F(p,t)+H(t,p).

В этом случае говорят, что разметка ' достижима из разметки , a  предшествует ' . Данный факт обозначается следующим образом: →t' .Сеть останавливается, если при некоторой разметке не может сработать ни один из ее переходов. Такая разметка называется тупиковой. Таким образом, СП-моделирует некоторую структуру и динамику ее функционирования.

Если разметка ' достижима из разметки  в результате срабатывания последовательности переходов r=t1,t2,...,tk , где: r - слово из множества Т* всех слов в алфавите Т , то это обозначается как →t1'''→t2... →''→ tk ' или →r'. Разметка  достижима в сети N, если 0→. Множество всех достижимых разметок в сети N обозначим через R(N). Переход t достижим от разметки  (→t) в ceти N, если:

 ' ''({ ',  ''}R(N)& - '):  '→ T ''.

Переход t достижим в сети N, если 0→t. В приложении к моделированию систем проблема достижимости разметки ' из 0 интерпретируется как возможность достижения определенного состояния системы.

Переход t живой, если:

R(N): →t.

СП живая, если:

t (tT&R(N)):  (p) →t.

Позиция р ограничена, если существует такое наперед заданное К, для которого R(N):  (p)<=K.

СП ограничена, если:

p (рp&r(n)):  (p)<=K.

Если к=1, то СП называется безопасной.

В настоящее время одним из наиболее широко используемых методов анализа СП является построение дерева достижимых разметок.

Дерево достижимых разметок представляет собой ориентированный граф, множество вершин которого образовано множеством R(N), причем из вершины  в вершину ' ведет дуга, помеченная символом перехода t , если и только если → t '. В общем случае дерево достижимых разметок может иметь бесконечное число вершин. Алгоритм построения конечного дерева достижимости включает в себя следующие этапы

Каждая i-я вершина дерева связывается с расширенной раз­меткой (i). В расширенной разметке число меток в позиции мо­жет быть либо неотрицательным целым, либо бесконечно большим. Бесконечное число меток обозначим символом  . Каждая вершина классифицируется или как граничная, терминальная, дублирующая вершина, или как внутренняя. Граничными являются вершины, которые еще не обработаны алгоритмом. После обработки граничные вершины становятся либо терминальными, либо дублирующими, либо внутренними. Алгоритм начинает свою работу с определения начальной разметки. До тех пор, пока имеются граничные вершины, они обрабатываются алгоритмом.

Пусть x - граничная вершина, которую необходимо обработать, и с которой связана разметка  (X).

1. Если в дереве имеется другая вершина y , не являющаяся граничной, и с ней связана разметка  (y)=  (x), то вершина x дублируется.

2. Если для разметки  (x) на один из переходов неразрешим, т.е.  (x) тупиковая разметка, то x терминальная вершина.

3. Для любого перехода tj, из множества T разрешенного в разметке  (x) , создать новую вершину z дерева достижимости. Разметка  (z), связанная с этой вершиной, определяется для каж­дой позиции рi следующим образом:

а) если  (x)i=, то  (z) i =;

б) если на пути от корневой вершины к x существует вершина y такая, что

 (y) →tj (x),  (y)<  (x) и  (y)i< (x)i, то  (z)i=;

в) в противном случае  (z)i= (x)i.

Дуга, помеченная tj, направлена от вершины х к вершине z. Вершина x переопределяется как внутренняя, вершина z становится граничной. Когда все вершины дерева становятся терминальными, дублирующими или внутренними, алгоритм останавливается.

Задание

1. .Описать следующую сеть Петри.

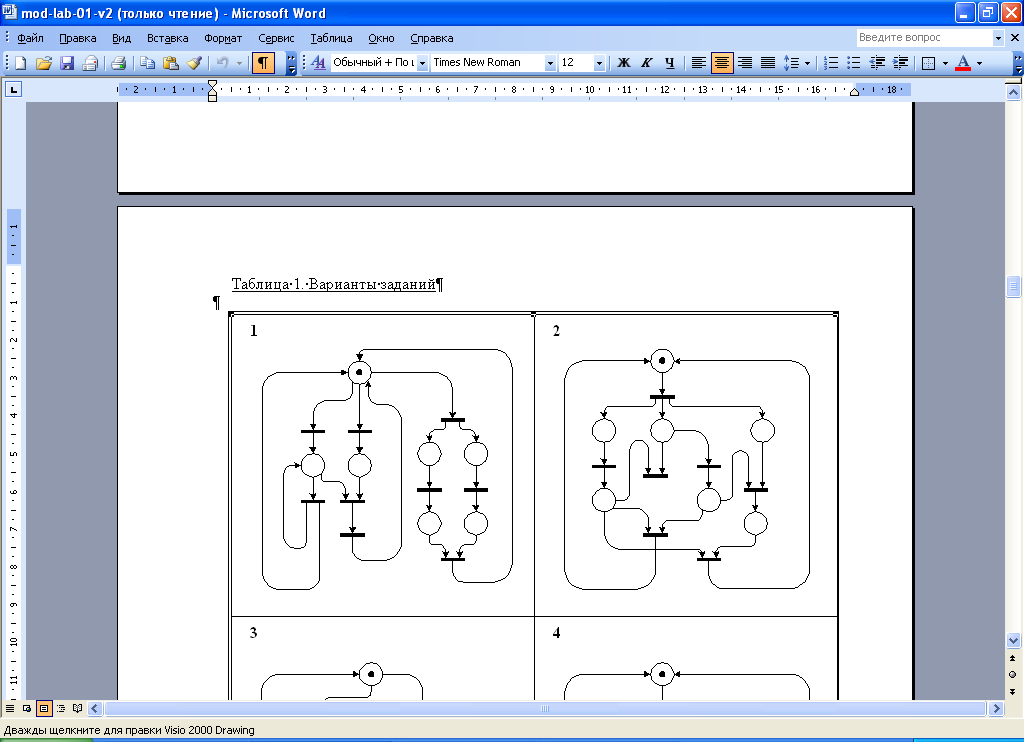
2. Написать программу реализации метода ДДР. Применить метод к заданной схеме. Провести исследование СП-модели путем построения дерева достижимых разметок (ДДР) вручную и с использованием полученной программы. Сравнить полученные результаты.

3. Оценить корректность СП-модели и предложить варианты устранения недостатков в случае их обнаружения. Допускается добавление новых элементов и ограниченно видоизменять топологию сети. Полученная модель должна соответствовать требованиям живости и безопасности.

3. Сдать отчет по работе.