Лабораторная работа 5 Методы восходящего анализа

1. Цель работы:

   1. Изучить принцип восходящего разбора.

   2. Построить дерево восходящего разбора применительно к грамматикам.

2. Литература:

   1. Молчанов А.Ю. Системное программное обеспечение. – СПб.: Питер, 2006. – 395с.

   2. Свердлов С.З. Языки программирования и методы трансляции. – СПб.: Питер, 2007. – 637с.

   3. Тонаненбаум Э. Компьютерные сети. – СПб.: Питер, 2008 – 991с.

   4. Сырецкий Г.А. Информатика. Фундаментальный курс. Том 1, 2. – Москва, 2005- 234с.

   5. Душин В.К. Теория основных информационных процессов и систем. – Москва, 2009 – 348 с.

   6. Русская компьютерная библиотека. URL: http://www.rusdoc.ru

3. Основное оборудование:

   1. ПЭВМ.

   2. Среда разработки Паскаль, С++, Delphi 7.

4. Задание:

   1. Изучить теоретический материал по теме «Методы синтаксического анализа языка».

   2. Выполнить задания, построить дерево восходящего разбора.

   3. Составить отчет по работе.

5. Порядок выполнения работы:

   1. Запустить среду разработки.

   2. Выполнить следующие задания:

Теоретические сведения

При восходящем разборе дерево начинает строиться от терминальных листьев путем подстановки правил, применимых к входной цепочке, в общем случае, в произвольном порядке. На следующем шаге новые узлы полученных поддеревьев используются как листья во вновь применяемых правилах. Процесс построения дерева разбора завершается, когда все символы входной цепочки будут являться листьями дерева, корнем которого окажется начальный нетерминал. Если, в результате полного перебора всех возможных правил, невозможно построить требуемое дерево разбора, то рассматриваемая входная цепочка не принадлежит данному языку.

Восходящий разбор также непосредственно связан с любым возможным выводом цепочки из начального нетерминала. Однако, эта связь, по сравнению с нисходящим разбором, реализуется с точностью до "наоборот".

Задание

Построить схему дерева вывода методом восходящего разбора по следующим грамматикам.

1. G6 = ({S}, {a, +, *}, P, S),

2. G3 = ({E, T, F}, {a, +, *, (,)}, P, E) где

P:

E T

E  E + T

T  F

T  T * F

F  (E)

F  a.

3. G4 = ({B, C, S}, {a, b, c}, P, S) где

P:

S  aSBC;

S  abc;

CB  BC;

bB  bb;

bC  bc;

cC  сc,

порождает язык { a ⁿ b ⁿ c ⁿ }, n ≥ 1.

Написать программу, реализующую метод восходящего разбора и позволяющую просмотреть схему дерева вывода.

3. Сдать отчет по работе.

6. Содержание отчета:

   1. Наименование работы.

   2. Цель работы.

   3. Схема грамматик восходящего разбора.

   4. Ответы на контрольные вопросы.

7. Контрольные вопросы:

   1. В чем заключается механизм восходящего разбора?

   2. Что называется грамматикой?

   3. Что называется порождающей грамматикой?

   4. Какой символ называется нетерминальным?

   5. Каким образом строится дерево при восходящем разборе?

Лабораторная работа 6 Реализация методов верификации программ

1. Цель работы:

   1. Изучить методы верификации программ.

   2. Провести анализ и доказательство правильности программы.

2. Литература:

   1. Молчанов А.Ю. Системное программное обеспечение. – СПб.: Питер, 2006. – 395с.

   2. Свердлов С.З. Языки программирования и методы трансляции. – СПб.: Питер, 2007. – 637с.

   3. Тонаненбаум Э. Компьютерные сети. – СПб.: Питер, 2008 – 991с.

   4. Сырецкий Г.А. Информатика. Фундаментальный курс. Том 1, 2. – Москва, 2005- 234с.

   5. Душин В.К. Теория основных информационных процессов и систем. – Москва, 2009 – 348 с.

   6. Русская компьютерная библиотека. URL: http://www.rusdoc.ru

3. Основное оборудование:

   1. ПЭВМ.

   2. Среда разработки Паскаль, С++, Delphi 7.

4. Задание:

   1. Изучить теоретический материал по теме «Верификация программ ».

   2. Выполнить задания.

   3. Составить отчет по работе.

5. Порядок выполнения работы:

   1. Запустить среду разработки.

   2. Выполнить следующие задания:

Теоретические сведения

1.Принцип математической индукции. 

Математическая индукция представляет собой общий способ доказательства. Он положен в основу всех приемов доказательства правильности программ для ЭВМ.

2.Принцип строгой индукции.

Пусть S(n) – некоторое высказывание о целом числе n и требуется доказать, что S(n) справедливо для всех положительных n. Для этого необходимо:

1. Доказать, что справедливо S(1);

2. Доказать, что если справедливы высказывания S(1), S(2), …, S(n) для всех положительных n, то справедливо S(n+1).

3.Принцип обобщенной индукции.

Метод математической индукции можно обобщить и применять не только для доказательства высказываний о множестве положительных целых чисел, но и о более общих множествах некоторых объектов.

Пусть Х – вполне упорядоченное (см. Практическое занятие №2) относительно < множество, а S(x) – некоторое высказывание, касающееся элемента х Х. Если требуется доказать справедливость S(x) для всех х Х, то необходимо:

1. Доказать, что справедливо S(х₀), где х₀ – наименьший элемент в Х.

2. Доказать для всех х Х, удовлетворяющих условию х₀ < x, что если справедливо S(у) для всех у < x, то справедливо и S(х).

Пример 1. Множество всех упорядоченных пар неотрицательных целых чисел вполне упорядоченно с помощью отношения лексикографического порядка <. Это отношение определяется так: отношение (n₁, n₂) < (n₃, n₄) справедливо, если и только если (n₁ < n₃) или (n₃ = n₁ и n₂ < n₄). Рассмотрим последовательность чисел, определенную следующим образом: S_0,0 =0, а для любой другой пары неотрицательных чисел n, m

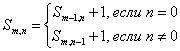
Доказать, что S_m,n = n+m для любых неотрицательных целых чисел n, m.

Применим принцип обобщенной индукции на множестве Х упорядоченных пар неотрицательных целых чисел <m, n>:

1. Так как пара <0, 0> - наименьший элемент Х, очевидна справедливость п. 3.1.

2. Пусть S_p,q = p + q для <p, q> < <m, n> (гипотеза индукции). Доказать, что S_m,n = m + n.

Если n = 0, то S_m,n = S_m-1,n + 1. Однако <m-1, n> < <m, n>, следовательно, S_m-1,n = m – 1 + n. Поэтому S_m,n = S_m-1,n +1 = m +n. Если n 0, S_m,n = S_m,n-1 + 1 по определению. Но <m, n-1> < <m, n> и по гипотезе S_m,n = m + n -1. Следовательно, S_m,n = S_m,n-1 + 1 = (m+n-1) + 1 = m + n.

4.Метод индуктивных утверждений

Метод индуктивных утверждений независимо сформулирован К. Флойдом и П. Науром. Суть этого метода состоит в следующем:

1) формулируются входное и выходное утверждения: входное утверждение описывает все необходимые входные условия для программы (или программного фрагмента), выходное утверждение описывает ожидаемый результат;

2) предполагая истинным входное утверждение, строится выведенное утверждение, которое выводится на основании семантики операторов, расположенных между входом и выходом (входным и выходным утверждениями);

3) формулируется теорема (условия верификации): из выведенного утверждения следует выходное утверждение;

4) доказывается теорема, что свидетельствует о правильности программы (программного фрагмента).

Пусть А – утверждение, описывающее предполагаемые свойства данных в программе, а С - утверждение, описывающее то, что по предположению требуется получить в результате выполнения программы (утверждение о правильности). Программа частично правильна, если при каждом ее выполнении с данными, удовлетворяющими предположению А, будет справедливо утверждение С при условии, что программа закончится.

Программа полностью правильна, если она частично правильна и заканчивается при всех данных удовлетворяющих предположению А.

5.Доказательство правильности программ с помощью индуктивных утверждений

Для доказательства частичной правильности утверждение А связывается с началом программы, а утверждение С с конечной точкой программы. Выявляются закономерности, относящиеся к значениям переменных, и связываются соответствующие утверждения (условия верификации), по крайней мере, с одной из точек в каждом цикле. Для каждого пути в программе, ведущего из точки i, связанной с утверждением А_i, в точку j, связанную с утверждением А_j, (при условии, что на этом пути нет точек с какими-либо дополнительными утверждениями), необходимо доказать, что если происходит попадание в точку i и справедливо с утверждение А_i, а затем производится проход от точки i до точки j, то при попадании в точку j будет справедливо с утверждение А_j. Для циклов точки i и j могут быть одной и той же точкой.

Для доказательства полной правильности программы сначала нужно доказать ее частичную правильность, а затем уже доказать, что программа когда-нибудь завершится.

Алгоритм доказательства правильности программы методом индуктивных утверждений:

1) Построить структуру программы.

2) Выписать входное и выходное утверждения.

3) Сформулировать для всех циклов индуктивные утверждения.

4) Составить список выделенных путей.

5) Построить условия верификации.

6) Доказать условие верификации.

7) Доказать, что выполнение программы закончится.

7.Аксиоматическое доказательство частичной правильности программ.

Утверждения, сформулированные на языке исчисления предикатов, используются для доказательства частичной правильности программ. При этом следует доказать истинность триады Хоара {Q} S {R}, где предикат Q - предусловие или входное утверждение для программы (фрагмента программы) S, предикат R - постусловие или выходное утверждение.

8.Правила верификации К. Хоара.

A1. Аксиома присваивания: {R_o} x := e {R}

A2. Если {Q} S {P} и {P} => {R}, то {Q} S {R}

A3. Если {Q} S {P} и {R} => {Q}, то {R} S {P}

Пусть S - это последовательность из двух операторов S1; S2 (составной оператор).

A4. Если {Q} S1 {P1} и {P1} S2 {R}, то {Q} S {R}.

Очевидно, что это правило можно сформулировать для последовательности, состоящей из n операторов. Правило для условного оператора (краткая форма).

A5. Если {Q AND B} S1 {R} и {Q NOT B} => {R}, то {Q} if B then S1 {R}.

Правило для альтернативного оператора (полная форма условного оператора ).

A6. Если {Q AND B} S1 {R} и {Q NOT B} S2 {R}, то {Q} if B then S1 else S2 {R}.Правила для оператора цикла until.

A7. Если {Q AND NOT B} S1 {Q}, то {Q} repeat S1 until B {Q AND NOT B} Правила для оператора цикла while.

A8. Если {Q AND B} S1 {Q}, то {Q} while B do S1 {Q AND NOT B}

Задание1

Доказать для n ⁴ 0 свойство чисел Фибоначчи, у которых f_n+1 = f_n + f_n-1, f₀ = 0, f₁ = 1

1.f₀ + f₁ + … + f_n = f_n+2 – 1

2.f_n a^n-1

3.Оператор 1: I = I₀, 2: I M, 3: I = F(I), T поменялись местами F

Задание 2

Написать программу реализации поиска и перечисления всех слова заданного предложения, в которые входят первые три буквы в первом слове предложения.

Доказать методом индуктивных утверждений правильность написанной программы.

3. Сдать отчет по работе.