
- •Техническое, информационное и программное обеспечение асу
- •Системный подход в асу. (Степин, Швечков)
- •Задачи и этапы системного анализа.(Швечков)
- •Общая классификация систем. Характеристики сложных систем.(Швечков)
- •Структуры управления производством. Функциональная структура асу. Состав и структура основных обеспечивающих частей асу. (Степин,Швечков)
- •Основные этапы и стадии создания и внедрения асу. Тз, тэо, тп и рп. (Степин)
- •Опытная эксплуатация
- •Промышленная эксплуатация
- •Сетевое планирование и управление (Швечков).
- •Архитектура и функционирование систем типа scada (Митичкин).
- •Функционирование системы scada.
- •Структурный и объектно-ориентированный подходы в проектировании ис (Кузнецова)
- •Объектно-ориентированный подход
- •Стандарты и классификация erp-систем. (Кузнецова)
- •Case-технологии. Современные case-средства. (Кузнецова)
- •Универсальный язык моделирования uml (Кузнецова)
- •Принципы моделирования
- •Сущности в uml
- •Общие механизмы uml
- •Виды диаграммUml
- •Сппр, их структура и место в асу. (Степин)
- •Деловые игры в разработке и внедрении асу. Методы согласования (выбора) групповых решений. (Степин)
- •Метод оценки результатов деловой игры:
- •Структура деловой игры
- •Этапы жизненного цикла программ и стандарт 15298. (Степин)
- •Методы управления производством. Функции управления и виды работ при управлении (Степин)
- •Экономические методы управления
- •1. Планирование
- •Организационно-распорядительные методы управления
- •Организационные методы воздействия
- •Экспертные оценки и обработка результатов экспертизы. (Степин)
- •Методика построения решения задач в асу. Методы оценки эффективности асу. (Степин)
- •Основные характеристики надежности невосстанавливаемых систем. (Толстов) Вероятность отказа.
- •Основные характеристики надежности восстанавливаемых систем. (Толстов)
- •Резервирование систем и элементов. (Толстов)
- •Структурные и функциональные методы тестирования программ. Методы оценки надежности
- •Защита информации в асу: основные понятия, этапы построения и принципы проектирования систем защиты (Леонов).
- •Практические подходы к созданию и поддержанию информационной безопасности. Управленческие и организационные мероприятия. (Леонов).
- •I. Управленческие мероприятия
- •Криптографические методы защиты. Симметричные и асимметричные алгоритмы шифрования, цифровая подпись. (Леонов).
- •Центр генерации ключей
- •II. Асимметричное шифрование
- •Средства обеспечения сетевой защиты: межсетевые экраны, системы обнаружения атак, системы анализа защищенности. (Леонов).
- •Основные типы межсетевых экранов
- •2. Шлюзы сеансового уровня
- •Основные схемы сетевой защиты на базе межсетевых экранов
- •1. Межсетевой экран - Фильтрующий маршрутизатор
- •Классификация систем обнаружения атак по принципу реализации
- •Системы анализа защищенности
- •Выбор топологии сети передачи данных. Методы маршрутизации сообщений в сетях.
- •Задача о максимальном потоке на сети. Определение кратчайшего пути на сети. (Командровский)
- •Операционные истемы реального времени. (Свистунов)
- •1. Основные понятия
- •2. Среда разработки и среда исполнения
- •3. Основные характеристики ос рв
- •Время реакции на события
- •Стандарт posix. Расширении posix реального времени. (Свистунов)
- •Аппаратно-программное обеспечение мультимедиа в иас. (Гарзанов)
- •Мультимедийная поддержка «живых» презентаций (Гарзанов)
- •Основные направления развития искусственного интеллекта. (Григорьев)
- •Анализ моделей представления знаний. Представление знаний правилами и логический вывод. Представление знаний фреймами, семантическими сетями, на основе логики предикатов. (Григорьев)
- •Структура и типы экспертных систем, их роль и место в асу. (Григорьев)
- •Экспертные системы реального времени (Степанкина)
- •Механизмы логического вывода в экспертных системах. Язык Пролог. (Степанкина)
- •Основы языка Пролог.
- •Терминология
- •Основные модели нейронов и нейронных сетей: структура, методы и алгоритмы обучения нс, области применения. (Григорьев, Юдовский)
- •Нечеткие системы и методы определения функций принадлежности. (Степин)
- •Методы определения функции принадлежности:
- •2. Экспертный метод.
- •3. Аналитический метод.
- •Дерево целей и дерево решений (Степин)
- •Генетические алгоритмы. (Степин)
- •Динамические системы. Модели представления в пространстве состояний. Модели "Выход-вход". (Григорьев)
- •Переход от временной к частотной области.
- •Переход от частотной области к временной.
- •Агрегативные системы. Агрегативный подход к моделированию сложных систем. (Григорьев)
- •Агрегат
- •Методология имитационного моделирования (принципы и методы). (Григорьев)
- •2.Имитация случайных величин с заданным законом распределения.
- •Основные понятия и определения теории графов. Графы специального вида: полный, пустой, регулярный, двудольный. Операции над графами. (Швечков)
- •Методы построения сетевого графика. Алгоритмы поиска критического пути и ключевых работ.(Швечков)
- •Нахождение кратчайших путей в графе. Потоки в сетях.(Швечков)
- •Многокритериальные модели оптимизации, их применение в задачах проектирования асу. (Степин)
- •Общая задача линейного программирования, ее каноническая форма, примеры применения. Симплекс-метод решения задач линейного программирования. (Свистунов)
- •Постановка и решение задач целочисленного линейного программирования. Алгоритмы "ветвей и границ" для решения задач целочисленного программирования. (Свистунов) .
- •Задачи выпуклого программирования. Метод неопределенных множителей Лагранжа. (Свистунов)
- •Транспортная задача (Свистунов)
- •Построение первоначального опорного плана
- •Метод динамического программирования и его применение в задачах распределения ресурсов. (Свистунов)
- •Алгоритмы численного решения задач безусловной оптимизации ( Свистунов)
- •Классификация методов
- •Общая характеристика методов нулевого порядка
- •Алгоритмы численного решения задач условной оптимизации (Свистунов)
- •Задачи нечеткого математического программирования. Задача выбора вариантов проектов. (Степин) Классификация и общая характеристика.
- •Задача достижения нечетко определенной цели (подход Беллмана—Заде).
- •Классификация задач нечеткого математического программирования.
- •Игровые модели принятия решений в асу. Методы решения задач теории игр. (Степин)
- •Случайные процессы. Марковские случайные процессы. Цепи Маркова с дискретным и непрерывным временем.( Степин )
- •Марковские случайные процессы.
- •Теория массового обслуживания. Системы массового обслуживания (разомкнутые, замкнутые). Определение характеристик типовых смо и их эффективности. (Степин)
- •Одноканальная система массового обслуживания.
- •Методы и модели получения случайных величин с заданным законом распределения на эвм, методы генерации случайных чисел. (Григорьев)
- •Имитация с. В. С заданной функцией плотности
- •Построение регрессионных моделей. Оценки параметров регрессионных моделей методом наименьших квадратов. (Григорьев)
- •Корреляционный анализ. (Григорьев)
- •Методы математической статистики (оценка параметров, доверительные интервалы, критерии согласия). (Григорьев)
- •Модели планирования эксперимента. (Григорьев)
- •Равновесие Неша и Парето в игровых моделях принятия решений (Степин)
- •Теория статистических решений (игры с природой) (Степин)
- •Теория статистических решений (игры с природой): критерии Севиджа, Вальда, Гурвица. (Степин)
- •Критерий Гурвица. Ориентация на самый худший исход является своеобразной перестраховкой, однако опрометчиво выбирать и излишне оптимистичную политику. Критерий Гурвица предлагает некоторый компромисс:
- •Методы решения игр с природой ( идеальный и неидеальный эксперимент). (Степин)
- •При решении статистических игр с единичным экспериментом возможно провести идеальный, либо неидеальный эксперимент.
- •Идеальный – это такой эксперимент, который полностью выясняет состояние «природы».
- •Неидеальный эксперимент уточняет вероятности (в смысле Байеса).
- •Инвариантность и устойчивость в управлении. . (Григорьев)
- •Проблема адекватности моделей . (Григорьев)
Методы построения сетевого графика. Алгоритмы поиска критического пути и ключевых работ.(Швечков)
Исходные данные= сетевой график разработки АСУ.
Возникает задача определения оптимальной очередности (контроля)результатов проектирования. Формализация задачи выглядит следующим образом:
1)Сеть разработки АСУ представлена графом G(I,Q), в котором вершины изображают события i=1…I, вершина- событие и результат выполнения работ.
Q-совокупность дуг графа (работ по проектированию); Q={qij}
2)Каждая дуга (работа) характеризуется некоторым временем tij и вероятностью Pij ошибочного принятия решения при выполнении работы.
Pij обычно определяется экспертным путем.
3)Будем считать (переномеруем события в графе так, что) i<j (упорядочим работу) и введем переменную xij.
1,если при завершении работы ij проводится анализ
Xij=0,в других случаях
1,если при наступлении события i(завершения работы ij)проводится контроль
Хi=0,в других случаях
4)Можно ввести управление U(x1,x2,…xq), которое состоит:
xq:xij-контроль по работам;xi-контроль по событиям
Контроль надо проводить так, чтобы minmax Tg(U)
U g
g={pij}-множество вероятности pij.
T-max срок окончания всех видов работ.
Алгоритм Дейкстры решает задачу о кратчайших путях из одной вершины для взвешенного орграфа G=(V, E) с исходной вершиной s, в котором веса всех дуг неотрицательны (w(u, v) ≥ 0 для всех (u, v) Є E). Перед тем, как рассматривать непосредственно алгоритм Дейкстры рассмотрим понятие релаксации. Техника релаксации состоит в следующем. Для каждой вершины v Є V мы храним некоторое число d[v], являющееся верхней оценкой веса кратчайшего пути из s в v. Начальное значение оценки кратчайшего пути и массива p устанавливается следующим образом:
для всех вершин v Є V[G] d[v] = ∞ p[v] = NULL d[s] = 0 |
Релаксация дуги (u, v) Є E состоит в следующем: значение d[v] уменьшается до d[u] + w(u, v), если второе значение меньше первого, при этом d[v] остаётся верхней оценкой. Также мы хотим, чтобы значение p[v] указывало путь, использованный при получении этой верхней оценки, поэтому одновременно мы изменяем значение p[v]. Фактически, если кратчайший путь проходит через какую-то вершину vi Є V отличную от s, то p[vi] будет указывать вершину из которой мы пришли в вершину vi.
Relax(u, v, w) if d[v] > d[u] + w(u, v) d[v] = d[u] + w(u, v) p[v] = u |
На рисунке 1 приведены два примера релаксации: в первом случае оценка кратчайшего пути уменьшается, во втором - нет.
|
Теперь рассмотри сам алгоритм нахождения кратчайшего пути. В процессе работы алгоритма Дейкстры поддерживается множество вершин S принадлежащих V, состоящее из вершин v, для которых уже найден кратчайший путь из вершины s - δ(s, v). Алгоритм выбирает вершину u Є V \ S с наименьшим d[u], добавляет u к множеству S и производит релаксацию всех дуг, выходящих из u, после чего цикл повторяется. Условно алгоритм можно записать следующим псевдокодом:
1. |
Инициализация: для всех вершин v Є V[G]: d[v] = ∞ и p[v] = NULL; d[s] = 0; |
2. |
S = NULL, Q = V[G]; |
3. |
Если в Q не осталось вершин, то конец алгоритма; |
4. |
Выбрать вершину u Є Q для которой d[u] - минимально и удалить её из Q; |
5. |
Добавить u в S; |
6. |
Для всех вершин v смежных с u выполнить релаксацию дуг (u, v); |
7. |
Перейти к шагу 3. |
После выполнения данного алгоритма длина кратчайшего пути из вершины s в v будет находится в d[v], а сам путь можно восстановить с помощью массива p. На рисунке 2 показаны несколько итераций работы алгоритма Дейкстры.
|
Первоначально кратчайшее растояние до всех вершин равно ∞, а расстояние от начальной вершины s до неё же равно 0. Вершина s имеет минимальную оценку кратчайшего расстояния на первой итерации, поэтому релаксацию проходят дуги (s, u) и (s, x). Красные стрелки на рисунке показывают текущие кратчайшие пути до вершин прошедших релаксацию, а также содержимое массива p (p[x] = s, т.к. предыдущей вершиной в кратчайшем пути проходящим через x была вершина s) . На второй итерации проходим вершину x, так как d[x] - минимально. Таким образом проходим все вершины.
Алгоритм Флойда.
![]()
Дано: непyстой взвешенный гpаф G=(V, E) с пpоизвольными весами ребер (дуг). Требуется найти длины кpатчайших пyтей между всеми парами вершин графа, если в графе нет циклов (контуров) отрицательной суммарной длины, либо обнаружить наличие таких контуров.
Инициализация:
1. Построим матрицу D0 размерности |V| x |V|, элементы которой определяются по правилу:
dii0= 0;
dij0= Weight(vi, vj), где i<>j, если в графе существует ребро (дуга) (vi, vj);
dij0= бесконечность , где i<>j, если нет ребра (дуги) (vi, vj).
2. m:=0.
Основная часть:
1. Построим матрицу Dm+1 по Dm, вычисляя ее элементы следующим образом: dijm+1=min{dijm, di(m+1)m + d(m+1)jm}, где i<>j; diim+1=0 (*). Если dimm + dmim < 0 для какого-то i, то в графе существует цикл (контур) отрицательной длины, проходящий через вершину vi; ВЫХОД.
2. m:=m+1; если m<|V|, то повторяем шаг (1), иначе элементы последней построенной матрицы D|V| равны длинам кратчайших путей между соответствующими вершинами; ВЫХОД.
ВНУТРИ
Если требует найти сами пути, то перед началом работы алгоритма построим матрицу P с начальными значениями элементов pij=i. Каждый раз, когда на шаге (1) значение dijm+1 будет уменьшаться в соответствии с (*) (т.е. когда di(m+1)m + d(m+1)jm<dijm), выполним присваивание pij:=p(m+1)j. В конце работы алгоритма матрица P будет определять кратчайшие пути между всеми парами вершин: значение pij будет равно номеру предпоследней вершины в пути между i и j (либо pij=i, если путь не существует).
Примечаниe: если граф - неориентированный, то все матрицы Dm являются симметричными, поэтому достаточно вычислять элементы, находящиеся только выше (либо только ниже) главной диагонали.

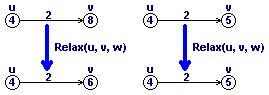 Рисунок
1 - Пример релаксации.
Рисунок
1 - Пример релаксации.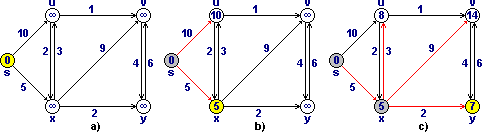 Рисунок
2 - Работа алгоритма Дейкстры.
Рисунок
2 - Работа алгоритма Дейкстры.