110) List the ordered pairs in the relation on {1, 2, 3} corresponding to the matrix (where the rows and columns correspond to the integers listed in increasing order).
{(1,1) (1,2) (1,3) (3,1)}
111) List the triples in the relation {(a, b, c) | a, b and c are positive integers with 1 < a + b < c ≤ 3}
(1,1,3)
112) A relation s on a set b is reflexive if
A relation R
on a set A
is called reflexive if
(a, a)
R for every element
.
113) A relation s on a set b is called antisymmetric if
A relation R
on a set A
such that
and
only if a = b,
for
,
is called antisymmetric.
114) Let R = {(1, 2), (2, 1), (2, 3), (3, 2), (4, 1), (4, 4)}. Find R2.
{(1,1) (1,3) (2,2) (3,1) (3,3) (4,2) (4,1) (4,4)}
115) Let R = {(1, 1), (1, 2), (2, 1), (3, 3), (2, 4), (4, 2), (4, 4)} be a relation on {1, 2, 3, 4}. The relation R is
116) Let R = {(a, b) | a ≤ b} be a relation on the set of integers. The relation R is
117) Let R = {(1, 3), (2, 1), (3, 2), (4, 3), (4, 4)}. Find R3.
118) Let R1 = {(a, b) | a = b + 2} and R2 = {(a, b) | a + b ≤ 3} be relations on {0, 1, 2, 3}. Find R1 – R2.
R1={(2,0)(3,1)} R2={(0,3)(1,2)(2,1)(3,0)} R1-R2={(2,0)(3,1)}
119) Represent the relation R= {(0, 0), (0, 2), (1, 1), (1, 3), (2, 0), (2, 2), (2, 3), (3, 0), (3, 3)} on {0, 1, 2, 3} with a matrix (with the elements of this set listed in increasing order).
1 0 1 0
0 1 0 1
1 0 1 1
1 0 0 1
120) List the ordered pairs in the relation on
{1, 2, 3, 4} corresponding to the matrix
(where the rows and columns correspond to the integers listed in
increasing order).
R={(1,3)(1,4)(2,1)(3,1)(3,2)(3,3)(3,4)(4,1)(4,2)}
121) Which of the following relations on {0, 1, 2, 3} is an equivalence relation?
122) Which of the following are posets?
123) Find two incomparable elements in the poset (P({1, 2, 3}), ).
124) Let S = {0, 1, 2, 3}. With respect to the lexicographic order based on the usual “less than” relation find all pairs in S S less than (2, 1).
{(0,0) (0,1) (0,2) (0,3) (1,0) (1,1) (1,2) (1,3) (2,0)}
125) Find maximal elements of the poset ({1, 2, 3, 5, 6, 13, 15, 30, 45, 60}, |). (13 45 60)
126) Find minimal elements of the poset ({2, 3, 5, 6, 7, 9, 30, 45, 54}, |). {2,3,5,7}
127) Find the lexicographic ordering of the following strings of lowercase English letters: compute, computable, commandos, competition.
commandos, competition, computable, compute
128) Which of the following sets is the equivalence class of 2 for congruence modulo 3?
[2]3={…-7,-4,-1,2,5,8,11…}
129) Let S = {1, 2, 3, 4, 5, 6, 7}. Which of the following collections of sets forms a partition of S?
130) Find the greatest element of the poset ({2, 4, 5, 6, 10, 24, 25, 50, 100}, |). No element
131) Find the least element of the poset ({2, 3, 5, 6, 9, 18, 36}, |). No element
132) Find the lexicographic ordering of the following 5-tuples: (1, 1, 1, 0, 1), (1, 1, 1, 1, 0), (0, 1, 0, 1, 0), (0, 1, 1, 0, 1), (1, 1, 0, 0, 0).
(0, 1, 0, 1, 0) (0, 1, 1, 0, 1) (1, 1, 0, 0, 0) (1, 1, 1, 0, 1) (1, 1, 1, 1, 0)
133) Find maximal elements of the poset ({2, 4, 6, 7, 8, 14, 20, 21, 42, 72}, |).
20,42,72 (PS no greatest)
134) Find minimal elements of the poset ({2, 3, 4, 7, 8, 9, 21, 36, 72}, |).
2,3,7 (PS no greatest, no least)
135) Find the greatest element of the poset ({2, 3, 6, 7, 42, 126, 252}, |).
252
136) Find the least element of the poset ({1, 5, 10, 11, 25, 55, 77, 111}, |).
1
137) Find two incomparable elements in the poset (P({a, b, c}), ).
138) Which of the following relations on the set of all people is an equivalence relation?
139) Which of the following sets is the equivalence class of 4 for congruence modulo 5?
[4]5={…-6,-1,4,9,14…}
140) An element a of a poset (S, ≤) is called maximal if
An element a
of a poset
is called maximal if
there is no
such that
.
141) How many edges are there in an undirected graph with 6 vertices each of degree 5?
2e=6*5
e=15
142) How many edges are there in an undirected graph having 5 vertices each of degree 3 and 7 vertices each of degree 5?
2e=5*3+7*5
e=25
143) Which of the following simple graphs does exist?
144) A simple graph differs from a multigraph since
A simple graph
consists of V,
a nonempty set of vertices,
and E, a
set of unordered pairs of distinct elements of V,
called edges.
A multigraph
consists of a set V of
vertices, a set E
of edges, and a function f from
E to
.
145) A pseudograph differs from a multigraph since
A pseudograph
consists of a set V of
vertices, a set E
of edges, and a function f from
E to
.
146) A directed graph differs from a directed multigraph since
A directed graph consists of a set V of vertices and a set E of edges that are ordered pairs of elements of V.
A directed multigraph consists of a set V of vertices, a set E of edges, and a function f from E to .
147) The union of two simple graphs
and
is
The union
of two simple graphs
and
is the simple graph with vertex set
and edge set
.
The union of G1
and G2
is denoted by
.
Example. Find the union of the graphs G1 and G2.
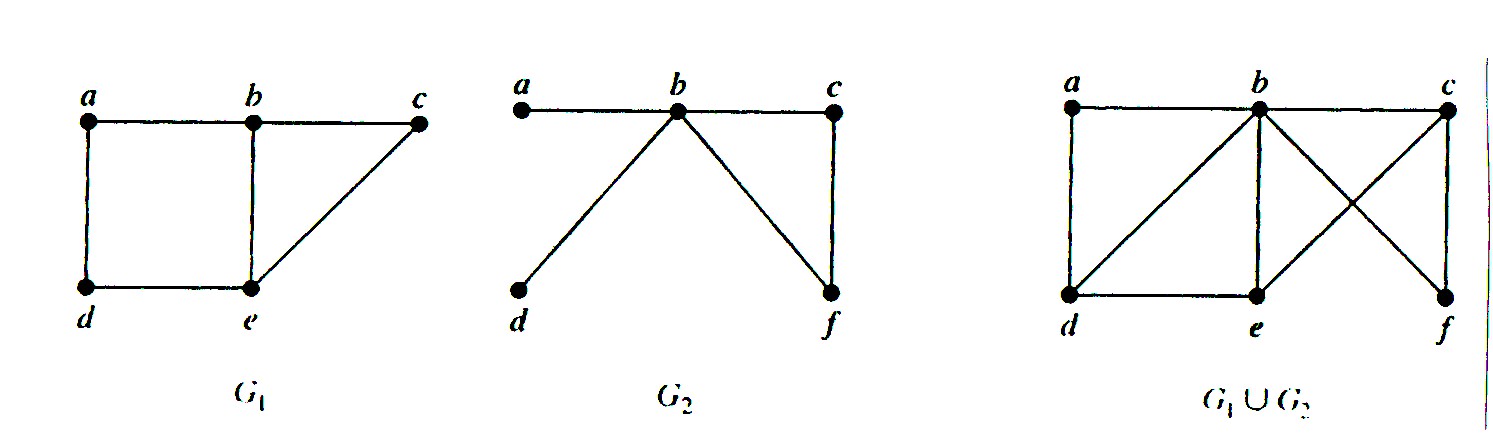
Solution: The vertex set of the union is the union of the two vertex sets, namely, {a, b, c, d, e, f}. The edge set of the union is the union of the two edge sets.
148) A subgraph of a graph G = (V, E) is …
When edges and vertices are removed from a graph, without removing endpoints of any remaining edges, a smaller graph is obtained. Such a graph is called a subgraph of the original graph.
A subgraph of
a graph
is a graph
where
and
.