Задание 4. Решение прямой угловой засечки по формулам Юнга.

Рассмотрим расчет координат удаленной точки по формулам Юнга. Даны точки 1 и 2 с координатами x1, y1 и x2, y2, соответственно. Кроме этого с помощью угломерного инструмента измерены два угла и (рис. 10).

При решении геодезических задач в отличие от общепринятых вычислений предполагается, что оси координат ох и оу переставлены местами (см. рис.1).

Рис. 10. Расчет координат по формулам Юнга.

Р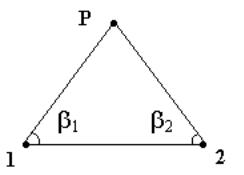 асчет координат точки Р можно выполнить по формулам:

Исходные данные:

1.Расчет в Microsoft Excel

Рассмотрим решение тестового примера по расчету координат удаленной точки по формулам Юнга с помощью программы MS Excel.

Спланируем вычисления так, что координаты x1, y1 и x2, y2 поместим в ячейки A2, B2, C2, D2. Если угол задавать в трех ячейках (градусы, минуты, секунды с долями), например в E2, F2 и G2, то угол в градусах с долями получается использованием формулы в H2: =E2+F2/60+G2/3600. Аналогично, для , используя для ввода ячейки I2, J2, K2, а для формулы L2: =I2+J2/60+K2/3600.

Для расчета координат по формулам Юнга требуется в ячейки А4 и D4 поместить формулы:

=(A2/TAN(РАДИАНЫ(L2))+C2/TAN(РАДИАНЫ(H2))-B2+D2)/(1/TAN(РАДИАНЫ(H2))+1/TAN(РАДИАНЫ(L2)))

и =(B2/TAN(L2*ПИ()/180)+D2/TAN(H2*ПИ()/180)+A2-C2)/

(1/TAN(H2*ПИ()/180)+1/TAN(L2*ПИ()/180)).

Здесь TAN – функция, предназначенная для вычисления тангенса угла. Эта функция используется, потому что ctgα=1/tgα. Функция TAN должна действовать на аргумент, выраженный в радианах. Это можно сделать либо используя функцию РАДИАНЫ (так сделано в формуле для xp), либо используя умножение на /180 (так сделано в формуле для yp).

Проверка (рис.11)

2.Расчет в Mathcad

Решение задачи вычисления координат удаленной точки по формулам Юнга можно произвести с использованием следующего кода:

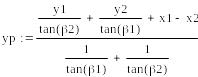
Функции ctg(β) в Mathcad нет, поэтому мы заменяем ctg( на .

3. Расчет в MatLab

Решение задачи вычисления координат точки по формулам Юнга можно произвести с использованием следующей последовательности операторов:

% расчет по формулам Юнга

clc

x1=input('x1->');

y1=input('y1->');

x2=input('x2->');

y2=input('y2->');

b1g=input('b1(grad)->');

b1m=input('b1(min)-->');

b1s=input('b1(sec)-->');

b2g=input('b2(grad)->');

b2m=input('b2(min)-->');

b2s=input('b2(sec)-->');

b1=b1g+b1m/60+b1s/3600 ; b2=b2g+b2m/60+b2s/3600;

b1=b1*pi/180 ; b2=b2*pi/180;

xp=(x1*cot(b2)+x2*cot(b1)-y1+y2)/(cot(b1)+cot(b2))

yp=(y1*cot(b2)+y2*cot(b1)+x1-x2)/(cot(b1)+cot(b2))

x1->47

y1->48

x2->54

y2->51

b1(grad)->48

b1(min)-->13

b1(sec)-->45.4

b2(grad)->48

b2(min)-->44

b2(sec)-->5.6

xp = 52.2254

yp = 45.5599

4.Расчет в Visual Basic

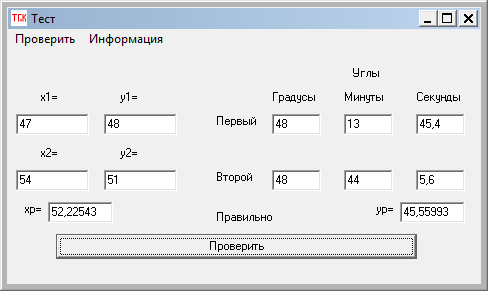
Рис. 12. Вид формы для решения задачи о вычислении координат по формулам Юнга.

Рассмотрим решение примера по расчету координат удаленной точки по формулам Юнга с помощью Visual Basic. Будем исходить из того, что координаты двух вершин и два угла треугольника заданы. Будем помещать их в поля окна программы.

Запустим систему Visual Basic. Через окно свойств изменим значение свойства Caption для формы со значения Form1 на расчет координат по формулам Юнга. Поместим на форму одну командную кнопку. Через окно свойств зададим значение свойства Caption равным Расчет. Поместим на форму десять компонентов TextBox, разместив около каждого из них по компоненту Label (рис. 12). Через окно свойств свойство TextBox каждого компонента TextBox заполним соответствующим значением координат точек и величин углов (например, из тестового примера, разделитель между целой и дробной частью - точка). Подписи полей ввода созданы с помощью компонентов Label, а именно в свойство Caption поместим: x1, y1 и т.д. Выполним два быстрых щелчка на кнопке Расчет. Тем самым будет создан каркас процедуры обработки события, возникающего при нажатии на кнопку:

Private Sub CommandButton1_Click()

End Sub

Между этими двумя строками необходимо поместить операторы, производящие расчет координат по формулам Юнга. При расчетах требуется вычислять функцию котангенс. В VBA нет стандартной математической функции котангенс. В этом случае можно воспользоваться выражением этой функции через косинус и синус. Прежде чем, запрограммировать расчет в процедуре обработки события, поместим перед описанием этой процедуры функцию:

Function ctg(x)

ctg = Cos(x) / Sin(x)

End Function

Эту функцию будем теперь использовать в процедуре обработки события. Сначала необходимо прочитать введенные в поля значения координат и углов. Для координат первой вершины это можно сделать с помощью конструкций:

X1 = Val(TextBox1.Text): Y1 = Val(TextBox2.Text)

Двоеточие между двумя конструкциями выполняет роль разделителя между операторами, когда они помещены в одну строку. Для координат второй вершины x2, y2:

X2 = Val(TextBox6.Text): Y2 = Val(TextBox7.Text)

Значение углов в градусах, минутах и секундах с долями может быть введено с помощью операторов:

b1 = Val(TextBox3.Text) + Val(TextBox5.Text) / 60 + Val(TextBox4.Text) / 3600

b2 = Val(TextBox8.Text) + Val(TextBox9.Text) / 60 + Val(TextBox10.Text) / 3600

После ввода координат и углов, введя постоянную величину pi = 3.1415926 необходимо выполнить перевод углов из градусов в радианы:

b1 = b1 * Pi / 180: b2 = b2 * Pi / 180

Затем следует вычислить величину координат:

xp = (X1 * ctg(b2) + X2 * ctg(b1) - Y1 + Y2) / (ctg(b1) + ctg(b2))

yp = (Y1 * ctg(b2) + Y2 * ctg(b1) + X1 - X2) / (ctg(b1) + ctg(b2))

Здесь ctg означает обращение к функции, описанной в программе. После последних вычислений необходимо выдать результат на форму. Это можно сделать с помощью операторов:

Label12.Caption = "xp= " + Str(xp)

Label13.Caption = "yp= " + Str(yp)

Таким образом, вся процедура будет иметь вид:

Private Sub CommandButton1_Click()

X1 = Val(TextBox1.Text): Y1 = Val(TextBox2.Text)

X2 = Val(TextBox6.Text): Y2 = Val(TextBox7.Text)

b1 = Val(TextBox3.Text) + Val(TextBox5.Text) / 60 + Val(TextBox4.Text) / 3600

b2 = Val(TextBox8.Text) + Val(TextBox9.Text) / 60 + Val(TextBox10.Text) / 3600

Pi = 3.1415926

b1 = b1 * Pi / 180: b2 = b2 * Pi / 180

xp = (X1 * ctg(b2) + X2 * ctg(b1) - Y1 + Y2) / (ctg(b1) + ctg(b2))

yp = (Y1 * ctg(b2) + Y2 * ctg(b1) + X1 - X2) / (ctg(b1) + ctg(b2))

Label12.Caption = "xp= " + Str(xp)

Label13.Caption = "yp= " + Str(yp)

End Sub

В результате вычислений для тестового примера получаем результат, представленный на рис. 12.

Видно, что получаются те же значения, которые были получены при проведении расчетов при помощи электронных таблиц, MathCad и MatLab.