- •Задание 1. Рассчитать величины углов треугольника, зная координаты его вершин.
- •1. Расчет в Microsoft Excel
- •1.Длина стороны ab вычисляется по формуле:
- •2.Длина стороны bc вычисляется по формуле:
- •3.Длина стороны ac вычисляется по формуле:
- •2. Расчет в Mathcad
- •3. Расчет в MatLab
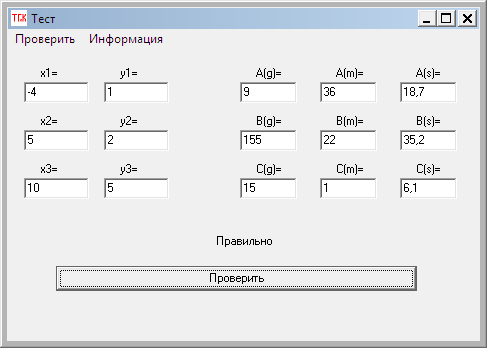
- •4. Расчет в Visual Basic
- •Задание 2 Расчет неприступного расстояния.
- •Расчет в Microsoft Excel
- •Расчет в Mathcad
- •3. Расчет в MatLab
- •4. Расчет в Visual Basic
- •Задание 3. Расчет превышения
- •Исходные данные:
- •1. Расчет в Microsoft Excel
- •Расчет в Mathcad
- •3. Расчет в MatLab
- •4. Расчет в Visual Basic
- •Задание 4. Решение прямой угловой засечки по формулам Юнга.
- •Исходные данные:
- •1.Расчет в Microsoft Excel
- •2.Расчет в Mathcad
- •3. Расчет в MatLab
- •4.Расчет в Visual Basic
- •Задание 5 Решение прямой угловой засечки по формулам Гаусса.
- •Исходные данные:
- •Расчет в Microsoft Excel
- •Расчет в Mathcad
- •Расчет в MatLab
- •4 . Расчет в Visual Basic
- •Задание 6 Решение обратной геодезической задачи.
- •Расчет в Microsoft Excel
- •2. Расчет в Mathcad
- •3. Расчет в MatLab
- •4. Расчет в Visual Basic
- •Задание 7 Решение обратной угловой засечки по формулам Пранис-Праневича.
- •Расчет в Microsoft Excel
- •Расчет в Mathcad
- •3.Расчет в MatLab
- •4 . Расчет в Visual Basic
- •Задание 8 Решение творческого задания для курсовой работы (Расчет токсичных выбросов в атмосферу при эксплуатации автомобилей)
- •Средние эксплуатационные нормы расхода топлива в л на 1 км пути
- •Заключение:
- •Список использованной литературы
- •Содержание
Министерство образования и науки Российской Федерации
НАЦИОНАЛЬНЫЙ МИНЕРАЛЬНО-СЫРЬЕВОЙ УНИВЕРСИТЕТ (ГОРНЫЙ)
КУРСОВАЯ РАБОТА
по ИНФОРМАТИКЕ
Тема:
РЕШЕНИЕ БАЗОВЫХ
ГЕОДЕЗИЧЕСКИХ ЗАДАЧ
Автор: студент гр. __ПГС-12__ _________ /Николаев Д. В./
(шифр группы) (подпись) (Ф.И.О.)
Оценка: ______________
Дата: ________________
Проверил:
руководитель работы доцент __________ /Глазков В.В./
(должность) (подпись) (Ф.И.О.)
Санкт-Петербург
2013 г.
Введение
Значительная часть работы геодезиста связана с проведением расчетов. В настоящее время основным вычислительным средством является персональный компьютер. Вычислительные возможности современных компьютеров реализованы как в программных средствах общего назначения, так и специализированном программном обеспечении.
В данной работе описываются основы использования вычислительных возможностей программ общего назначения в проведении геодезических расчетов. Рассказывается о проведении расчетов в Microsoft Excel, MathCad, MatLab и с помощью системы программирования Visual Basic.
Рассматриваются основные (базовые) геодезические расчеты: расчет расстояния до неприступной точки, вычисление превышения, решение обратной геодезической задачи, решение прямой угловой засечки по формулам Гаусса, решение прямой угловой засечки по формулам Юнга, решение обратной угловой засечки по формулам Пранис-Праневича.
Материал изложен так, что сначала приводятся расчетные схемы и формулы, а затем описываются средства и возможности различных программ. Решение всех задач ведется в соответствии с вариантом шестнадцатым.
Задание 1. Рассчитать величины углов треугольника, зная координаты его вершин.
Пусть треугольник задан координатами своих вершин (рис.1). Вычислим величины его углов. Ответ представим в градусах, минутах, секундах и их десятых долях.
Р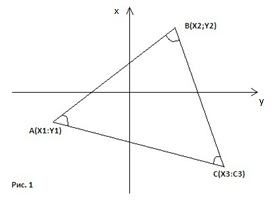 ис.
1. Треугольник, заданный координатами
своих вершин.
ис.
1. Треугольник, заданный координатами
своих вершин.
На рис. 1 система координат выбрана так, как это приято в геодезии.
В случае, когда
треугольник задан координатами своих
вершин, длины его сторон можно определить
по формулам вычисления расстояния между
двумя точками, заданными своими
координатами. Для стороны AB будем иметь:
![]() .
Для стороны BC
будем иметь: BC=
.
Для стороны BC
будем иметь: BC=![]() .
.
Для стороны AC будем иметь:
AC=![]() . Длины остальных
сторон вычисляются аналогично. По
известным длинам сторон треугольника
может быть вычислена его площадь. Для
этого можно использовать формулу Герона:
. Длины остальных
сторон вычисляются аналогично. По
известным длинам сторон треугольника
может быть вычислена его площадь. Для
этого можно использовать формулу Герона:
![]() ,
где
,
где ![]() -полупериметр
треугольника.
-полупериметр
треугольника.
Дальнейшее решение
этой задачи может быть основано на
использовании теоремы косинусов для
треугольника. Согласно этой теореме:
квадрат длины одной из сторон треугольника
равен сумме квадратов длин двух других
сторон без удвоенного произведения
этих сторон на косинус угла между ними.
Для стороны AB будем иметь: ![]() ,
,
для стороны BC
будем иметь: ![]() ,
для стороны AC
будем иметь:
,
для стороны AC
будем иметь: ![]()
Для косинусов углов будем иметь:
![]() ,
,
![]()
![]()
Для самих углов будем иметь формулы:
![]() ,
,
![]() ,
,![]()
Треугольник задан координатами своих вершин.
Таблица 1(исходные данные для задачи по нахождению величин углов треугольника)
x1 |
y1 |
x2 |
y2 |
x3 |
y3 |
-4 |
1 |
5 |
2 |
10 |
5 |
Вычислим величины его углов с помощью . Microsoft Excel, MathCad, MatLab и системы программирования Visual Basic. Ответ представим в градусах, минутах, секундах и их десятых долях.
1. Расчет в Microsoft Excel
Предположим, что
координаты вершин треугольника заданы
в ячейках ![]() (ячейки первой строки могут быть
заполнены поясняющими подписями). Если
запланировать ячейку G2, например, под
хранение длины стороны AB, то в нее
необходимо записать формулу (через
строку формул):
(ячейки первой строки могут быть
заполнены поясняющими подписями). Если
запланировать ячейку G2, например, под
хранение длины стороны AB, то в нее
необходимо записать формулу (через
строку формул):
=КОРЕНЬ((C2-A2)*(C2-A2)+(D2-B2)*(D2-B2))
Здесь используется функция вычисления квадратного корня, конструкция (C2-A2)*(C2-A2) соответствует возведению в квадрат выражения в скобках (можно было бы так же использовать конструкцию (C2-A2)^2).Итак:
1.Длина стороны ab вычисляется по формуле:
=КОРЕНЬ((C2-A2)*(C2-A2)+(D2-B2)*(D2-B2))
Получим, что AB=9,055385
2.Длина стороны bc вычисляется по формуле:
=КОРЕНЬ((E2-C2)*(E2-C2)+(F2-D2)*(F2-D2))
Получим, что BC=5,830952
3.Длина стороны ac вычисляется по формуле:
=КОРЕНЬ((E2-A2)*(E2-A2)+(F2-B2)*(F2-B2))
Получим, что AC=14,56022
Для вычисления величины угла А в ячейку J2 необходимо поместить формулу:
=(180/ПИ())*ACOS((G2*G2+I2*I2-H2*H2)/(2*G2*I2)).
Таким
образом,
угол
A вычислим
с
помощью
формулы
=(180/ПИ())*ACOS((G2*G2+I2*I2-H2*H2)/(2*G2*I2)),
![]() ,
угол
B вычислим
с
помощью
формулы
=(180/ПИ())*ACOS((H2*H2+G2*G2-I2*I2)/(2*H2*G2)),
,
угол
B вычислим
с
помощью
формулы
=(180/ПИ())*ACOS((H2*H2+G2*G2-I2*I2)/(2*H2*G2)),
![]() ,угол
C
вычислим с помощью формулы
=(180/ПИ())*ACOS((I2*I2+H2*H2-G2*G2)/(2*I2*H2)),
,угол
C
вычислим с помощью формулы
=(180/ПИ())*ACOS((I2*I2+H2*H2-G2*G2)/(2*I2*H2)),
![]() .
Для проверки расчетов в ячейку М2 следует
поместить формулу: =СУММ(J2:L2)
(через двоеточие в формулах указываются
диапазоны ячеек). Она будет вычислять
сумму углов треугольника. При правильности
вычислений она должна быть равна 180.
.
Для проверки расчетов в ячейку М2 следует
поместить формулу: =СУММ(J2:L2)
(через двоеточие в формулах указываются
диапазоны ячеек). Она будет вычислять
сумму углов треугольника. При правильности
вычислений она должна быть равна 180.
![]() =
=![]() +
+![]() +
+![]() =
=![]()
Для
получения градусов ![]() в ячейку N2 поместим формулу:
в ячейку N2 поместим формулу:
=ОКРВНИЗ(J2;1).Получили
![]() Для получения минут в ячейку O2 поместим
формулу:
Для получения минут в ячейку O2 поместим
формулу:
=ОКРВНИЗ((J2-N2)*60;1).Получили
![]() Для получения секунд с долями в P2 поместим
формулу: =(J2-(N2+O2/60))*3600.Получили
Для получения секунд с долями в P2 поместим
формулу: =(J2-(N2+O2/60))*3600.Получили
![]() .
Итак,
.
Итак, ![]()
Для
получения градусов ![]() в ячейку Q2
поместим формулу:
в ячейку Q2
поместим формулу:
=ОКРВНИЗ(K2;1).
Получили
![]() Для получения минут в ячейку R2
поместим формулу:
Для получения минут в ячейку R2
поместим формулу:
=ОКРВНИЗ((K2-Q2)*60;1).Получили
![]() Для получения секунд с долями в S2
поместим формулу:
Для получения секунд с долями в S2
поместим формулу:
=(K2-(Q2+R2/60))*3600.
Получили
![]() .
Итак,
.
Итак, ![]()
Для
получения градусов ![]() в ячейку T2
поместим формулу:
в ячейку T2
поместим формулу:
=ОКРВНИЗ(L2;1).Получили
![]() Для получения минут в ячейку U2
поместим формулу:
Для получения минут в ячейку U2
поместим формулу:
=ОКРВНИЗ((L2-T2)*60;1).Получили
![]() Для получения секунд с долями в V2
поместим формулу:
Для получения секунд с долями в V2
поместим формулу:
=(L2-(T2+U2/60))*3600.
Получим
![]() Итак,
Итак, ![]()
Проверка(рис 2.)