Министерство образования Российской Федерации

НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

кафедра «Атомные, тепловые станции и медицинская инженерия»

Гидравлический расчет трубопровода

Методические указания к выполнению курсовой работы по дисциплине «Механика жидкости и газа» для студентов дневной формы обучения специальности 1010, 1005, 1906, 0705

Нижний Новгород

2006

Составитель: Д.В.Спиридонов

УДК 532.51

Гидравлический расчет трубопровода:

Метод. указания к курсовой работе по курсу «Механики жидкости и газа» для студентов спец.1010, 1005, 1906 и 0705 дневной формы обучения /НГТУ; Сост.: Д.В.Спиридонов Н.Новгород, 2006. 18с.

Даны краткие теоретические сведения из гидравлики, описаны основные этапы и последовательность выполнения курсовой работы, порядок ее оформления.

Редактор ______________

Подп. к печ. 28.04.06. Формат 60×84 . Бумага газетная. Печать

Офсетная. Печ. л. 1,5. Уч.– изд.л. 0,6. Тираж 100 экз. Заказ

–––––––––––––––––––––––––––––––––––––

Нижегородский государственный технический университет

Типография НГТУ. 603 600, Н.Новгород, ул. Минина, 24

© Нижегородский государственный

технический университет, 2006

1. Цель работы

Изучить методы расчета основных типов трубопроводных систем.

2. Основы гидравлического расчета трубопроводов

Системы трубопроводов в настоящее время являются самым эффективным, надёжным и экологически чистым транспортом для жидких и газообразных продуктов.

2.1 Основные термины и определения

Простым трубопроводом называют трубопровод, по которому жидкость транспортируется без промежуточных ответвлений потока. Трубопровод может иметь постоянный диаметр по всей длине, или может состоять из последовательно соединенных участков разного диаметра.

Сложный трубопровод имеет разветвленные участки, состоящие из нескольких простых трубопроводов, между которыми распределяется жидкость, движущаяся внутри труб.

Узлами называются сечения трубопровода, в которых смыкаются несколько ветвей.

2.2 Гидравлический расчет простого трубопровода

Основным уравнением при расчетах простого трубопровода является уравнение баланса напоров или уравнение Бернулли. Рассмотрим участок простого трубопровода, изображенный на рисунке 1 и запишем уравнение Бернулли для сечений а и b этого трубопровода для случая установившегося движения жидкости:

(1)

где Z_a и Z_b – вертикальные координаты центров тяжести сечений а и b, м;

Р_а и Р_b – давление в центрах тяжести сечений а и b, Па;

_a и _b – коэффициенты кинетической энергии для сечений а и b;

V_a и V_b – среднерасходные скорости в сечениях а и b, м/с;

h_п – суммарная потеря напора между сечениями а и b трубопровода, включающая потери на трение по длине и потери на местных сопротивлениях, м.

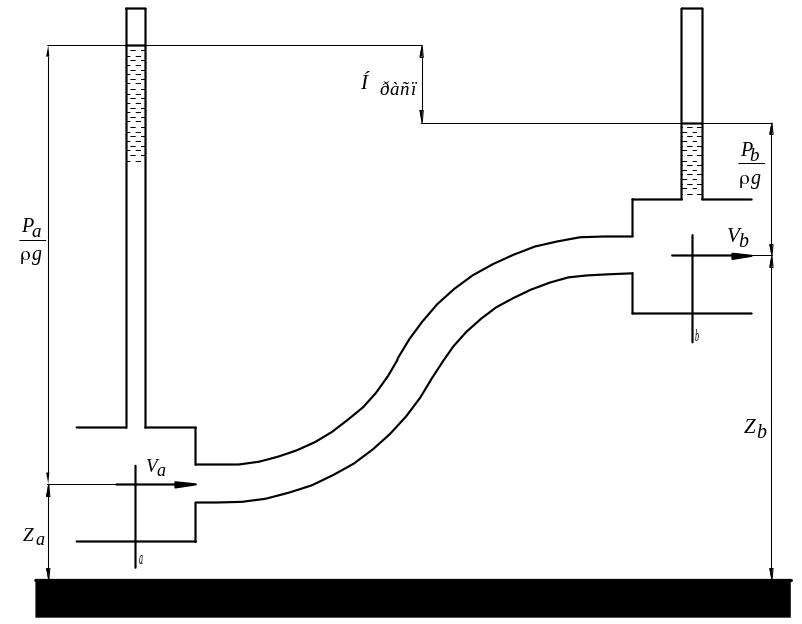
Рисунок 1 Участок простого трубопровода

Для удобства расчетов вводится понятие располагаемого напора трубопровода Н_расп:

(2)

Как видно из формулы, этот напор складывается из геометрической высоты Z = Z_b – Z_a на которую поднимается жидкость в процессе движения по трубопроводу и разности пьезометрических высот в начале и конце трубопровода.

Преобразуем уравнение баланса напоров (1) с учетом введенного понятия располагаемого напора и получим общий вид расчетного уравнения простого трубопровода:

(3)

Если площади поперечных сечений питателя и приемника значительно превосходят сечение трубопровода (трубопровод соединяющий два больших резервуара) или скорости в сечениях а и b одинаковы вследствие равенства их площадей проходного сечения (при условии, что _a = _b), скоростными напорами жидкости в этих сечениях можно при составлении баланса напоров пренебречь. При этом расчетное уравнение для располагаемого напора приобретает вид:

(4)

Уравнение (4) описывает процесс, в котором весь располагаемый напор затрачивается на преодоление гидравлических сопротивлений.

Уравнение (4) справедливо так же в тех случаях, когда трубопровод имеет достаточно большую длину, при которой скоростные напоры на входе и выходе из трубопровода оказываются пренебрежимо малыми по сравнению с потерями напора на трение по его длине.

Основной принцип расчета простых трубопроводов – это принцип суперпозиции потерь, согласно которому все последовательно соединенные элементы трубопровода работают независимо друг от друга и для определения полной потери напора все потери на отдельных элементах суммируются:

(5)

где – суммарные потери на трение по длине, м;

– суммарные потери на местных сопротивлениях, м.

Потери напора на трение на i-ом участке трубопровода определяются по известной формуле Дарси-Вейсбаха:

(6)

где _i – коэффициент сопротивления трения по длине,  = f(Re);

L_i и d_i – длина и диаметр трубы, м;

V_i – среднерасходная скорость потока в трубе, м/с.

Потери напора на i-ом местном сопротивлении определяются по общей формуле:

(7)

где _i – безразмерный коэффициент местного сопротивления;

V_i – среднерасходная скорость потока в характерном сечении трубы, м/с.

Таким образом, расчет трубопровода на основе уравнения (4) связан с выбором коэффициентов местных сопротивлений _i и коэффициентов сопротивления трения _i. Рекомендации по определению коэффициентов _i приводятся в [1]  [3]. Значения некоторых коэффициентов местных сопротивлений _i для турбулентного режима приведены в приложении 1, а более подробные данные по местным сопротивлениям приведены в справочной литературе, например [4].

Основная цель решения уравнения (4) – это построение гидравлической характеристики трубопровода – зависимости суммарной потери напора (давления) в трубопроводе от расхода:

(8)

Гидравлическая характеристика трубопровода необходима для определения гидравлических характеристик питателя трубопроводной сети (например, напора или расхода насоса).

Рассмотрим возможные варианты расчета простого трубопровода.

Вариант 1. Дано: расход Q, свойства жидкости ( и ), геометрические характеристики трубопровода (длины и диаметры участков, геометрия местных сопротивлений), а также материал и качество поверхности трубы  (шероховатость). Найти требуемый напор Н_расп.

Решение. По известным Q, d,  находится число Рейнольдса

Re = 4Q/(d) (9)

и определяется режим движения жидкости. Затем по соответствующим формулам (или опытным данным) оценивают местные сопротивления при ламинарном и при турбулентном течении жидкости. Далее по числу Re и значению шероховатости стенок трубопровода  определяют коэффициент  и, наконец, решают основное уравнение (4) относительно Н_расп.

Вариант 2. Дано: располагаемый напор Н_расп, свойства жидкости ( и ), геометрические характеристики трубопровода (длины и диаметры участков, геометрия местных сопротивлений), а также материал и качество поверхности трубы  (шероховатость). Найти расход Q.

Решение. Определяют режим течения жидкости, основываясь на вязкости жидкости путем сравнения напора H с его критическим значением Н_кр, так как решение несколько различно для ламинарного и турбулентного течения:

(10)

где Re_кр – критическое число Re соответствующее переходу ламинарного течения в турбулентное.

Если H < H_кр, режим ламинарный, если Н > H_кр — турбулентный.

1. При ламинарном течении используют прием замены местных сопротивлений эквивалентными длинами , и задача решается относительно просто. Из уравнения (4), с учетом того при ламинарном режиме течения , а так же формул (6) и (9) находят расход Q. При этом в качестве длины трубопровода L подставляют приведенную длину трубопровода и методом последовательных приближений уточняются выбранные значения эквивалентных длин местных сопротивлений и приведенной длины трубопровода L_пр.

2. При турбулентном течении задачу надо решать методом последовательных приближений.

Уравнение (4) имеет два неизвестных Q и . Для решения задачи задают начальное значение коэффициента  с учетом шероховатости . Так как этот коэффициент изменяется в сравнительно узких пределах ( = 0,015  0,04), большой ошибки при этом не будет, тем более, что при дальнейшем определении Q коэффициент  оказывается под корнем.

Решая уравнение (4) с учетом выражений (5), (6) и (7) относительно Q, находят расход в первом приближении. По найденному Q определяют Re, а по Re — уже более точное значение . Снова подставляют полученное значение в то же основное уравнение и решают его относительно Q. Находя расход во втором приближении, получают большее или меньшее расхождение с первым приближением. Если расхождение велико, то расчет продолжают в том же порядке. Разница между каждым последующим значением Q и предыдущим будет все меньше и меньше.

Обычно бывает вполне достаточно двух или трех приближений для получения приемлемой точности.

Вариант 3. Дано: расход Q располагаемый напор Н_расп, свойства жидкости и все размеры трубопровода, кроме диаметра. Найти диаметр трубопровода d.

Решение. Определяют режим течения жидкости, основываясь на вязкости жидкости путем сравнения напора Н_расп с его критическим значением Н_кр:

(10)

где Re_кр – критическое число Re соответствующее переходу ламинарного течения в турбулентное.

Если Н_расп < H_кр, режим ламинарный, если Н_расп > H_кр — турбулентный.

Решая уравнение (4) с учетом выражений (5), (6) и (7) относительно d лучше всего выполнить следующим образом: задать ряд стандартных значений d и для заданного Q подсчитать ряд значений Н_расп. Затем построить график зависимости Н_расп от d и по заданному Н_расп по кривой определить d, выбрать больший ближайший стандартный диаметр и уточнить Н_расп.