Задание № 3. Критерии Вальда, Байеса-Лапласа, Сэвиджа и Гурвица
Обоснование состава ремонтной бригады. На предприятии решается вопрос о создании ремонтной бригады. Основываясь на применении критериев Вальда, Лапласа, Сэвиджа и Гурвица, определить наиболее целесообразное число членов бригады. Исходные данные сведены в табл. 27, в ячейках которой занесены доходы при разных вариантах (стратегиях). Под стратегией понимается x – число членов бригады и R – количество станков, требующих ремонта.
Вариант 3
Таблица 27
x\R |
40 |
30 |
20 |
10 |
5 |
60 |
100 |
180 |
250 |
4 |
90 |
90 |
80 |
230 |
3 |
210 |
190 |
100 |
210 |
2 |
200 |
220 |
210 |
150 |
Решение:
Критерий Вальда. Справа дописывается столбец минимумов по строкам.
|
|
|
|
|
|
|
|
40 |
30 |
20 |
10 |
|
Вальда |
5 |
60 |
100 |
180 |
250 |
|
60 |
4 |
90 |
90 |
80 |
230 |
|
80 |
3 |
210 |
190 |
100 |
210 |
|
100 |
2 |
200 |
220 |
210 |
150 |
|
150 |
|
|
|
|
|
|
150 |
Тогда
.
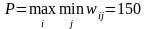Таким образом, при данных условиях
рациональным решением будет x=2.
2. Критерий Лапласа. Рассмотрим ситуацию, когда все состояния природы равновероятны. В этом случае критерий примет вид:
|
|
|
|
|
|
|
|
|
40 |
30 |
20 |
10 |
|
|
Лапласа |
5 |
60 |
100 |
180 |
250 |
|
|
147,5 |
4 |
90 |
90 |
80 |
230 |
|
|
122,5 |
3 |
210 |
190 |
100 |
210 |
|
|
177,5 |
2 |
200 |
220 |
210 |
150 |
|
|
195 |
|
|
|
|
|
|
|
195 |
Тогда
.
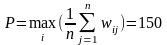Таким образом, наилучшим решением будет
x=2.
3.
Критерий
Сэвиджа.
Построим матрицу рисков. Ее элементы
определяются по формуле
,
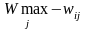где
.
|
Матрица Риска |
|
|
|
|
||||
|
40 |
30 |
20 |
10 |
|
Сэвиджа |
|||
5 |
150 |
120 |
30 |
0 |
|
150 |
|||
4 |
120 |
130 |
130 |
20 |
|
130 |
|||
3 |
0 |
30 |
110 |
40 |
|
110 |
|||
2 |
10 |
0 |
0 |
100 |
|
100 |
|||
|
|
|
|
|
|
100 |
|||
Тогда
.
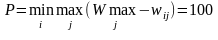Оптимальная стратегия согласно критерию
Сэвиджа x=2.
4. Критерий Гурвица. В отличие от примененных выше «жестких» критериев, критерий Гурвица является «гибким», так как позволяет варьировать «степень оптимизма-пессимизма». Таким образом, этот критерий устанавливает баланс между случаями крайнего оптимизма или пессимизма, путем введения коэффициента веса ρ.
Применим данный критерий к нашим исходным данным, полагая ρ =0.5.
|
Матрица Риска |
|
|
|
|
|
|
|
|
|
|||||||||
|
40 |
30 |
20 |
10 |
|
|
Гурвица |
|
|
||||||||||
5 |
150 |
120 |
30 |
0 |
|
|
60 |
250 |
155 |
|
|
||||||||
4 |
120 |
130 |
130 |
20 |
|
|
80 |
230 |
155 |
|
|
||||||||
3 |
0 |
30 |
110 |
40 |
|
|
100 |
210 |
155 |
|
|
||||||||
2 |
10 |
0 |
0 |
100 |
|
|
150 |
220 |
185 |
макс |
185 |
||||||||
|
|
|
|
|
|
|
min w |
mах w |
Р |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Коэффициент пессимизма |
0,5 |
|
|
|
|
|
|
||||||||||
Таким образом,
.
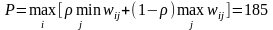Оптимальная стратегия x=2.