
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
Уфимский государственный авиационный технический университет
Кафедра вычислительной математики и кибернетики
Расчетно-графическая работа
по дисциплине «Методы оптимальных решений»
Вариант 3
Выполнил: студент группы ЭФ-401пз
Васильева Наталья
Проверил:
доцент каф. ВМиК Зотова О.Ф.
Уфа-2013
Задание № 1. Задача линейного программирования Вариант 1
Постановка задачи:
В кондитерском цехе выпускают печенье двух сортов. Расход продуктов на каждый из сортов представлен в таблице 1, также в таблице указан запас продуктов каждого вида.
Таблица 1
|
Масло |
Яйца |
Сахар |
Молоко |
Сорт 1 |
0,2 |
0,25 |
0,15 |
0,15 |
Сорт 2 |
0,1 |
0,2 |
0,2 |
0,25 |
Запас |
10 |
15 |
10 |
15 |
Доход от продажи 1 кг печенья 1 сорта 0,3 руб., 2 сорта – 0,2 руб. Какое количество печенья каждого сорта следует выпекать в сутки, чтобы доход был максимальным.
Математическая модель:
Запишем задачу в форме задачи линейного программирования.
Целевая функция:
Z = 0.3x1+0.x2→max
Z - 0,3x1+0,2x2=0
|
|

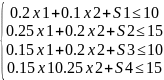
Решение:
Итерация 0.
БП |
x1 |
x2 |
S1 |
S2 |
S3 |
S4 |
Р-е |
От-е |
z |
-0,3 |
-0,2 |
0 |
0 |
0 |
0 |
0 |
- |
S1 |
0,2 |
0,1 |
1 |
0 |
0 |
0 |
10 |
50 |
S2 |
0,25 |
0,2 |
0 |
1 |
0 |
0 |
15 |
60 |
S3 |
0,15 |
0,2 |
0 |
0 |
1 |
0 |
10 |
67 |
S4 |
0,15 |
0,25 |
0 |
0 |
0 |
1 |
15 |
100 |
S1→x1
Итерация 1
БП |
x1 |
x2 |
S1 |
S2 |
S3 |
S4 |
Р-е |
От-е |
z |
0 |
-0,05 |
1,5 |
0 |
0 |
0 |
15 |
- |
x1 |
1 |
0,5 |
5 |
0 |
0 |
0 |
50 |
100 |
S2 |
0 |
0,075 |
-1,25 |
1 |
0 |
0 |
2,5 |
33,3 |
S3 |
0 |
0,125 |
-0,75 |
0 |
1 |
0 |
2,5 |
20 |
S4 |
0 |
0,175 |
-0,75 |
0 |
0 |
1 |
7,5 |
42,9 |
S3→x2
Итерация 2
БП |
x1 |
x2 |
S1 |
S2 |
S3 |
S4 |
Р-е |
z |
0 |
0 |
1,2 |
0 |
0,4 |
0 |
16 |
x1 |
1 |
0 |
8 |
0 |
-4 |
0 |
40 |
S2 |
0 |
0,075 |
-0,45 |
0 |
0,6 |
0 |
1,5 |
x2 |
0 |
1 |
-6 |
0 |
8 |
0 |
20 |
S4 |
0 |
0 |
-1,8 |
0 |
-1,4 |
1 |
4 |
Ответ:
В z-строке все коэффициенты неотрицательны, следовательно, получено оптимальное решение x1=40, x2=20, Zmax=16.
