Показатели безотказности невосстанавливаемых систем

В качестве случайной величины T примем наработку до отказа (единственного для систем данного класса). Считаем, что нам известна функция распределения F(t) , которая в данном случае будет называться функцией вероятности отказа Q(t), то есть

.

Важнейшим количественным показателем безотказности служит функция вероятности безотказной работы в течение заданного времени t:

.

Показатели безотказности можно оценивать приближенно по статистическим данным. Рассмотрим формулы для определения статистических значений показателей безотказности.

Статистическая оценка вероятности отказа

.

Статистическая оценка вероятности безотказной работы

.

Статистическая оценка плотности распределения наработки на отказ

.

Показатели безотказности восстанавливаемых систем

Восстанавливаемые системы имеют поток отказов и периодически подвергаются воздействию системы технического обслуживания и ремонта (рис. 1.9, где t_i – i-ая наработка на отказ, t_i – i-ое время восстановления после i-го отказа).

Вероятность безотказной работы с момента окончания (i-1)-го восстановления за период t

.

Средняя наработка на отказ за интервал времени от момента окончания (i-1)-го восстановления до наступления i-го отказа

.

Показатели сохраняемости

Средний срок сохраняемости – математическое ожидание случайной величины хранения до отказа:

.

Показатели ремонтопригодности

Свойство ремонтопригодности можно определять, как и все остальные свойства надежности, через соответствующие показатели, которые определяются через законы распределения длительности восстановления f_в(t) и F_в(t).

характеристики свойства ремонтопригодности применяют следующие:

– интенсивность восстановления

,

– среднее время восстановления

,

– вероятность восстановления в заданное время

.

34. Классические и топологические методы расчета надежности экономической информационной системы.

К классическим методам относятся модели надежности с последовательным, параллельным, параллельно-последовательным соединениями элементов, их различные модификации.

Модель с последовательным соединением элементов (рис. 2.1). При расчетах надежности последовательным называется такое соединение элементов, при котором отказ хотя бы одного из них приводит к отказу всего соединения в целом. Последовательное соединение в указанном выше смысле не всегда совпадает с физическим последовательным соединением элементов. Отказы элементов предполагаются независимыми, то есть отказ любой группы элементов никак не влияет на вероятностные характеристики остальных элементов. Элемент понимается как один из самостоятельных участков последовательного соединения.

Рис. 2.1. Последовательное соединение элементов

В данном случае вероятность безотказной работы системы можно рассчитать по формуле

,

где Р_с – вероятность безотказной работы системы; Р_i(t) – вероятность безотказной работы i-го элемента системы.

М одель с параллельным соединением элементов (рис. 2.2). При расчетах надежности параллельным (резервным) называется такое соединение элементов, при котором отказ всего соединения происходит при отказе всех элементов системы (элементы дублируют друг друга).

Рис. 2.2. Параллельное соединение элементов

В этом случае показатель надежности системы P_c определяется через вероятности отказа элементов q₁, q₂, …, q_n, которые связаны с вероятностью безотказной работы соотношениями вида

q_i(t) = 1 – P_i(t).

Вероятность отказа всей системы равна:

.

Тогда вероятность безотказной работы системы с параллельным соединением элементов q₁, q₂, …, q_n имеет вид

.

Модель с параллельно-последовательным соединением элементов. При расчетах надежности параллельно-последовательным называется такое соединение элементов, при котором можно составить структурные схемы участков как с последовательным, так и с паралелльным соединением элементов (рис. 2.3).

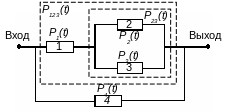
Рис. 2.3. Параллельно-последовательное соединение элементов

Для системы вначале рассчитывается вероятность безотказной работы участка 23

P₂₃ = 1 – (1 – P₂(t))(1 – P₃(t)),

затем для участка 123

P₁₂₃(t) = P₁(t)P₂₃(t) = P₁(t)(1 – (1 – P₂(t))(1 – P₃(t))) .

Итоговая расчетная формула имеет вид

P_с(t) = 1 – (1 – P₁₂₃(t))(1 – P₄(t)).

Модели, не сводимые к параллельно-последовательным соединениям. К данному классу относятся системы с мостовыми и еще более сложными соединениями элементов (рис. 2.4).

Рис. 2.4. Пример мостового соединения элементов

Система является работоспособной, если работоспособны элементы:

• 1,3 ;

• 2,4;

• ……….

• 1,5,4;

• 2,3,5;

Надежность систем данного класса целесообразно оценивать по логико-вероятностному методу, используя аппарат алгебры логики (см. раздел 2.3).

Топологический метод использует аппарат теории графов применительно к решению задач надежности.

Методика расчета показателей надежности топологическим методом в установившемся режиме, где топологические коэффициенты С_i для каждой x_i вершины графа определяются непосредственно по графу, а затем вычисляется нужный показатель по нижеприведенным топологическим формулам.

Для определения коэффициента С_i необходимо:

– выбрать начальную вершину графа x_q отдельно для определения каждого из коэффициентов С_i ( ); начальная вершина может быть выбрана произвольно, однако выбор влияет на объем вычислений, поэтому ее надо выбирать так, чтобы были длинные прямые пути;

– построить множество К прямых путей из начальной вершины x_q в вершину x_i, для которой определяется коэффициент;

– для каждого k-го прямого пути построить множество замкнутых контуров подграфа G{X_k} и образовать возможные комбинации независимых замкнутых контуров (множество соединений S), где G{X_k} – подграф графа G{X, W}, образованный удалением множества вершин, входящих в k-й путь, и прилегающих к нему дуг;

– записать коэффициенты C_i по найденным составляющим по формуле

,

гдe К – множество прямых путей из произвольно выбранной вершины х_q в х_i; Х_к – множество вершин, входящих в k-й прямой путь.

Используя топологические коэффициенты, основные показатели надежности установившегося режима можно записать:

вероятность нахождения системы в i-м состоянии

,

где n – число вершин графа;

35. Логико-вероятностные и структурные методы расчета надежности экономической информационной системы

Метод основан на математическом аппарате алгебры логики. Расчет надежности системы управления предполагает определение связи между сложным событием (отказ системы) и событиями, от которых оно зависит (отказы элементов). Следовательно, расчеты на надежность основаны на проведении операций с событиями и высказываниями, в качестве которых принимаются утверждения о работоспособности или отказе элемента (системы). Каждый элемент системы представляется логической переменной, принимающей значение 1 или 0.

События и высказывания при помощи операций дизъюнкции, конъюнкции и отрицания объединяются в логические уравнения, соответствующие условию работоспособности системы. Составляется логическая функция работоспособности. Расчет, основанный на непосредственном использовании логических уравнений, называется логико-вероятностным и выполняется в семь этапов:

1. Словесная формулировка условий работоспособности объекта. Описывается зависимость работоспособности ИС от состояния ее отдельных элементов.

2. Составление логической функции работоспособности. Представляет собой логическое уравнение, соответствующее условию работоспособности системы управления:

 , (2.2)

которое выражено в дизъюнктивной форме, например:

,

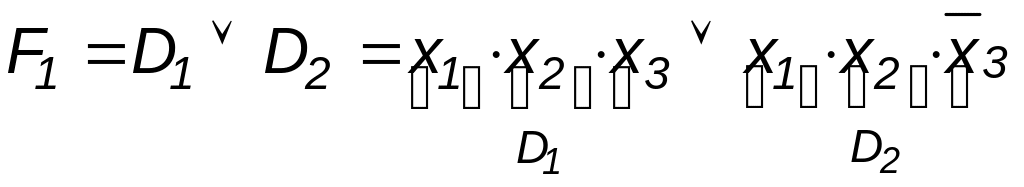где x_i – условие работоспособности i-го элемента F_л; (х_i = 1) – работоспособное состояние, (x_i = 0) – неработоспособное состояние.

3. Приведение логической функции работоспособности F_Л к ортогональной бесповторной форме F_ЛО. Сложную логическую функцию работоспособности необходимо привести к ортогональной бесповторной форме.

Функция вида (2.2) называется ортогональной, если все ее члены D_i попарно ортогональны (их произведение равно нулю), и бесповторной, если каждый ее член D_i состоит из х_i с разными номерами (отсутствуют повторяющиеся аргументы). Например,

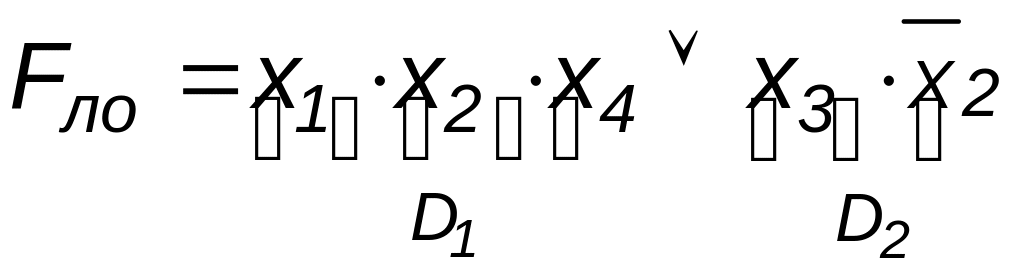 – ортогональная бесповторная форма,

 – ортогональная, но не бесповторная форма.

4. Арифметизация F_ло. По найденной ортогональной бесповторной логической функции работоспособности F_ЛО определяется арифметическая функция F_a (2.4).

,

, (2.4)

где A_i – арифметическая форма членов D_i функции F_ло.   Арифметизация членов D_i, в общем виде содержащих операции дизъюнкции, конъюнкции и отрицания, осуществляется заменой логических операций арифметическими по правилам:

1) ;

2) ;

3) .

5. Определение вероятности безотказной работы системы. Вероятность безотказной работы системы устанавливается как вероятность истинности логической функции работоспособности, представленной в ортогональной бесповторной форме, и вычисляется как сумма вероятностей истинности всех ортогональных членов этой функции алгебры логики. Все события (высказывания) заменяются их вероятностями (вероятностями безотказной работы соответствующих элементов).

.

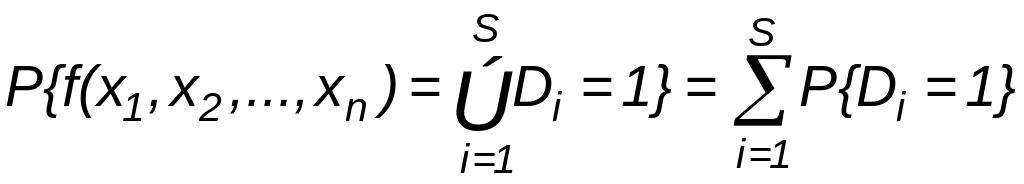6. Вычисление требуемых показателей надежности системы управления по найденному показателю P_c(t):

• вероятность безотказной работы P_c(t);

• вероятность отказа Q_c(t) = 1 – P_c(t);

• интенсивность отказов ;

• средняя наработка до отказа .

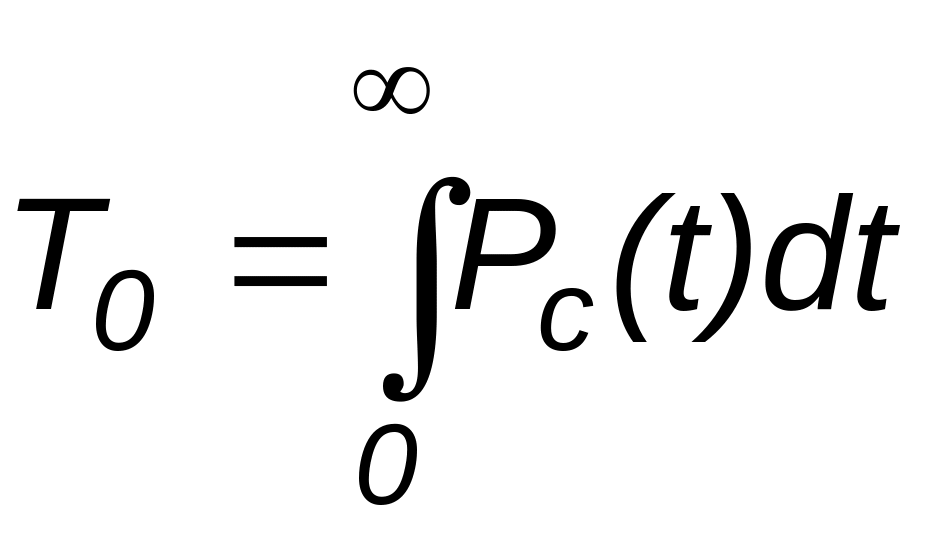7. Анализ соответствия полученных показателей надежности заданным техническим требованиям системы.

Допущения, принимаемые при логико-вероятностном методе: для элементов системы возможны только два состояния; метод применим для невосстанавливаемых систем; отказы элементов системы должны быть независимы.

36. Экспериментальная оценка надежности экономической информационной системы: общая характеристика

Под экспериментальной оценкой надежности понимается определение и контроль различных показателей по результатам испытаний или наблюдений в процессе эксплуатации.

Для проведения испытания составляются планы испытаний, в которых задаются характеристики:

– число систем, поставленных на испытание, N;

– порядок замены отказавших систем в процессе испытаний: Б – без замены отказавших систем на новые, В – с заменой отказавших систем на новые;

– продолжительность испытаний: r – испытания ведутся до отказа r (r<N) систем, если наработка t_r до появления r-го отказа t_r<T ; Т – испытания продолжаются определенное время Т, если t_r ≥T.

По результатам испытаний в зависимости от принятого плана формируется вариационный ряд наработок на отказ , где t_i – отказ i-й системы. Затем подсчитывается суммарная наработка на отказ, Т_∑r , через которую можно определить статистическую оценку показателей безотказности, например

Возможные планы испытаний: