Вопрос 5. Уравнение взаимного ориентирования, его практическое использование

Уравнение взаимного ориентирования – зависимости, связывающие ЭВзО с координатами одноимённых точек фотоснимков стереопары.

Уравнение взаимного ориентирования в общем виде:

R₀·(R₁*R₂) = 0

Где R₀ – вектор, определяющий положение точки S₂ в системе координат S₁XYZ; R₁ и R₂ – векторы, определяющие положение одноименных точек a₁ и a₂ в системах координат S₁XYZ и S₂XYZ (см. §8 в методичке).

Для ЭВзО первой системы X_S2 = B, Y_S2 = 0, Z_S2 = 0. Условие пересечения одноименных проектирующих лучей примет вид:

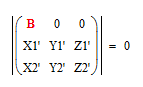
Если разложить определитель по элементам 1 строки, получим:

B(Y₁’Z₂’ – Y₂’Z₁’) = 0

Y₁’Z₂’ – Y₂’Z₁’ = 0 (т. к. B ≠ 0)

Где X₁’, Y₁’, Z₁’ – пространственные координаты одноименной точки левого фотоснимка в системе координат S₁X’Y’Z’, X₂’, Y₂’, Z₂’ – пространственные координаты одноименной точки правого фотоснимка в системе координат S₂X’Y’Z’

Эта зависимость и есть уравнение взаимного ориентирования первым способом.

Пространственные координаты равны:

X₁’ = a₁₁’x₁ + a₁₂’y₁ – a₁₃’f

Y₁’ = b₁₁’x₁ + b₁₂’y₁ – b₁₃’f

Z₁’ = c₁₁’x₁ + c₁₂’y₁ – c₁₃’f

X₂’ = a₂₁’x₁ + a₂₂’y₁ – a₂₃’f

Y₂’ = b₂₁’x₁ + b₂₂’y₁ – b₂₃’f

Z₂’ = c₂₁’x₁ + c₂₂’y₁ – c₂₃’f

Где:

a'_1i, b’_1i, c’_1i – направляющие косинусы-векторы ЭВзО α’₁, κ’₁ левого фотоснимка P₁ стереопары;

a'_2i, b’_2i, c’_2i – направляющие косинусы-векторы ЭВзО α’₂,ω’₂ κ’₂ правого фотоснимка P₂ стереопары

i = 1, 2, 3 – номера направляющих косинусов

С учетом значений пространственных координат точек фотоснимков, уравнение взаимного ориентирования примет вид:

(b₁₁’x₁ + b₁₂’y₁ – b₁₃’f)(c₂₁’x₁ + c₂₂’y₁ – c₂₃’f) – (b₂₁’x₁

6.Элементы внешнего (геодезического) ориентирования модели

Ориентирование модели от носительно геодезической СК и определение её масштаба на- зывается внешним (геодези-ческим) ориентированием модели. Величины, определяющие по- ложение модели относительно геодезической СК и её масш- таб, называются элементами внешнего ориентирования мо- дели (ЭВО модели).По-другому, эти величины определяют ориентировку фо-тограмметрической СК отно-сительно геодезческой СК.ЭВО модели показаны на рис.3

X_Го ,Y_Го ,Z_Го -геодезические координаты начала фотограмметрической системы координат (ЛЭВО модели). ξ, η, θ –УЭВО модели. t – масштабный коэффициет

Таким образом модель име- ет 7 ЭВО.Линейные ЭВО X_Го,Y_Го,Z_Го определяют положение начала фотограмметрической СК от- носительно геодезической.Угловые ЭВО ξ, η, θ задают повороты фотограмметричес-кой СК: ξ - продольный угол накло-на модели – угол в плоскости X_Г Z_Г осью Z_Го и проекцией оси Z на эту плоскость.η – поперечный угол наклона модели – угол между осью Z и её проекцией на плоскость X_Г Z_Г. θ – угол поворота модели – угол в плоскости X Y между осью Y и следом плоскости Y_ГZ. t – заменатель масштаба модели (масштабный коэф- фициент). Зная ЭВО модели, пред- ставляется возможным пе- рейти от фотограмметри-ческих координат точек мо- дели к геодезическим коорди- натам точек местности.