22.Внешнее ориентирование модели маршрута
Задача внешнего ориентирования свободной фотограмметрической сети решается по опорным точкам.Оно выпол-ся на основе ур-ий внешнего ориентирования, при этом требуется не менее 4 опорных точек,т.к.задача далжна решаться по методу наим квадратов и с контролем.
Последовательность внешнего ориентирования
Приближённое масштабирование модели маршрута.
Определение ЭВО модели маршрута.
Вычисление геодезических координат всех точек сети.
а) Приближённое масштабирование модели маршрута:
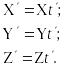
В
зависимостях (6.31) X',Y,'Z' фотограмметрические
координаты точек сети после масштабирования,
а X,Y,Z – координаты тех же точек (в
системе координат S1XYZ
точек) до масштабирования и t – масштабный
коэффициент.
Масштабный коэффициент определяют по формуле:
где DГ – расстояние между точками местности (в геодезической системе координат);
D – расстояние между соответствующими точками в фотограмметрической системе координат;
∆ΧГ,∆УГ,∆ZГ - приращения геодезических координат опорных точек;
∆Χ,∆У,∆Z - приращения фотограмметр. координат тех же точек.
б) Определение ЭВО модели маршрута:
Теоретическую основу способа составляют уравнения внешнего ориентирования модели :
Решение системы уравнений (7.19) по методу наименьших квадратов приводит к системе нормальных уравнений, из решения которой получают поправки к приближённым значениям неизвестных. Вычислительный процесс выполняется последовательными приближениями. В итоге будут получены ЭВО модели маршрута Χo , Yo,, Zo, η, θ, ξ , t.
в)Вычисление геодезических координат всех точек сети, в том числе и опорных точек, выполняется по тем же зависимостям (7.19). Исходными данными при этом служат фото- грамметрические координаты точек сети и вычисленные ранее ЭВО модели маршрута.
Кроме того, вычисленные высоты следует ис-править поправками за кривизну Земли, которые вычисляют по формуле:
В зависимости (6.16) D – расстояние от начала системы координат до данной точки, а R - радиус Земли.
23.Деформация модели маршрута под влиянием систематических ошибок
Накопление ошибок в маршрутной ф-ции описывается ф-ми:
где δXn δYn, δZn – суммарные ошибки координат точек n–ой Модели (в конце маршрута).
dXi, dYi, dZi – ошибки одиночных моделей с номером i (i=1,3,…, n).
Д
опустим,
что при построении маршрутной
фотограмметрической сети оказывают
влияние только систематические ошибки.
При равенстве базисов будем иметь
повторяемость ошибок одиночных моделей.
Поэтому
где ∆Х- систематическая ошибка абсцисс точек одиночной модели.
Т
огда
суммарную систематическую ошибку точек
n-й модели полу-чим на основании заисимостей
(6.8):
И
з
рис 2. видно, что
δΧс
равно:
или с учётом выражения
Аналогично получим ∆Yс и ∆Zс . В результате будем иметь: В зависимостях (7. 14)
∆X, ∆Y и ∆Z – систематические ошибки координат точек одиночной модели;
δXс, δYс и δZс – систематические ошибки координат точек в середине маршрута.
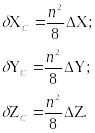
Ошибки одиночной модели описываются полиномами. Если подставить эти выражения вместо ошибок одиночных моделей в зависимости (7.14), то получим:
где А i, Bi , Ci – коэффициенты, характеризующие деформацию модели маршрута (i=0,1,2,3,4);
Ослабить влияние систематических ошибок и тем самым уменьшить необходимое количество опорных точек можно, используя элементы внешнего ориентирования фотоснимков. Если, например, в процессе построения фотограмметрической сети используют УЭВО фотоснимков, то уравнения её деформации имеют вид:
При совместном использовании плановых координат центров проекций и УЭВО фотоснимков деформация модели выражается зависимостями:
Устранение систематических ошибок в координатах точек сети
а) Определение коэффициентов полиномов:
Для системы уравнений (7.21) необходимо иметь шесть планово-высотных опорных точек, так как одна такая точка позволяет составить три уравнения вида (7.21), а неизвестных – 15. Решается система под условием [pv2]=min. В результате будут определены коэффициенты Ai,Bi,Ci (i=0,1,2,3,4).
б) Вычисление окончательных значений координат точек фотограмметрической сети
выполняется по формулам:
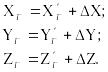
В зависимостях (7.22) поправки вычисляют с использованием ранее определённых коэффициентов полиномов и полученных после внешнего ориентирования геодезических координат точексети по формулам:
--В результате построения свободной фотограмметриче-ской сети аналитическим способом будут вычислены фото-граметрические координаты X, Y, Z всех точек, в том числе и опорных, в системе координат O(S)XYZ .
Для преобразования фотограмметрических координат в геодезические координаты, необходимо выполнить внешнее ориетирование свободной сети (модели маршрута) и устра-нение систематических ошибок.
Кроме того, необходимо исправить геодезические коорди-наты за влияние кривизны Земли, и в первую очередь необходимо исправить высоты точек