
- •Семестр 2
- •1. Статистика рабочей силы и рабочего времени предприятия
- •2. Календарный фонд. Производительность труда
- •В зависимости от измерения затрат труда различают следующие уровни производительности.
- •4. Основной капитал предприятия
- •1. По характеру участия в производственном процессе:
- •Равномерный метод.
- •Пример:
- •Метод дигрессивной нормы амортизации.
- •5. Оборотный капитал предприятия
- •Факторный анализ оборачиваемости оборотных активов.
Семестр 1 1. Виды средних величин и их расчеты |
|||||||||||||||||
Средняя величина представляет собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени. Средние величины исчисляются для характеристики уровня цен, заработной платы, основного капитала, численности населения и др. однородной совокупности социально-экономических явлений. Требования, предъявляемые к средним величинам: – средняя должна характеризовать качественно однородную совокупность; – средние должны исчисляться по данным большого числа единиц, составляющих совокупность, то есть отображать массовые социально-экономические явления. Для более глубокого научного анализа изучаемых явлений исчисляют средние величины не только всей совокупности, но и по составляющим эту совокупность. Задача статистики состоит в том, чтобы дать смысловую социально-экономическую оценку результатам расчетов средних показателей. Средняя величина всегда именованная, она имеет ту же размерность, что и признак у единиц совокупности. В экономических исследованиях применяются две категории средних: степенные средние и структурные средние. Таблица 3.1 Виды средних величин
х – индивидуальное значение признака, n – число значений признака.
К
степенным средним относятся: средняя
арифметическая, средняя гармоническая,
средняя геометрическая и средняя
квадратическая. Средняя
обозначается через Средняя арифметическая простая используется в тех случаях, когда варианты или варьирующие признаки встречаются только по одному разу и имеют одинаковый вес в совокупности. Средняя арифметическая взвешенная используется, когда данные сгруппированы, а отдельные значения признака встречаются неодинаковое число раз. Средняя гармоническая – это величина, обратная средней арифметической из обратных значений признака. Средняя гармоническая вычисляется в тех случаях, когда в качестве весов применяются не единицы совокупности, а произведения этих единиц на значения признака (то есть М=хf). Средняя гармоническая простая исчисляется в тех случаях, когда веса одинаковы, то есть равны между собой. Средняя геометрическая простая используется при вычислении среднего коэффициента роста (темпа роста) в рядах динамики. Средняя квадратическая используется для расчетов среднего квадратического отклонения () при изучении темы «Показатели вариации».
Для
вычисления средней
в дискретных рядах
варианты нужно умножить на частоты и
сумму произведений разделить на сумму
частот, то есть по средней арифметической
взвешенной Для вычисления средней в интервальных рядах нужно перейти к дискретному ряду, то есть по каждой группе вычислить значение интервала, заменить интервал его средним значением и вычислить по формуле
Для того чтобы проверить правильность выбора формул, надо учитывать: – среднее значение признака не должно выходить за пределы минимального и максимального значений признака совокупности; – среднее значение ближе к тому значению признака, которому соответствует большая частота. Степенные средние дают обобщающую характеристику совокупности и являются абстрактными величинами, полученными расчетным путем, в то же время эти средние не отражают всех особенностей совокупности, они могут быть различными для одинаковых совокупностей или иметь одинаковое значение для совокупности с различным строением. Структурные средние используются для более полной характеристики совокупности. К ним относятся: Мода – это варианта с наибольшей частотой (М0); Медиана – это варианта, делящая совокупность на две равные части (Ме). Квартили – это варианта, делящая совокупность на четыре равные части; Децили – это варианта, делящая совокупность на десять равных частей. Выбор вида средней величины в каждом конкретном случае определяется целью исследования и характером имеющихся данных. Для дискретного ранжированного ряда значения признака расположены в порядке возрастания или убывания, место медианы в ряду определяют по формуле
где n – число членов ряда. Если же ряд распределения состоит из четного числа членов, то за медиану принимают среднюю арифметическую из двух средних значений. В интервальном ряду мода определяется по формуле
где хм0 – нижняя граница модального интервала; fм0 – частота модального интервала; f(м0-1) – частота интервала, предшествующего модальному; f(м0+1) – частота интервала, следующего за модальным. В интервальном ряду распределения для нахождения медианы сначала указывают интервал, в котором она находится. Медианным является первый интервал, в котором сумма накопленных частот превысит половину общего числа наблюдений. Численное значение медианы вычисляется по формуле
где n – сумма частот ряда; Хме – нижняя граница медианного интервала; i – величина интервала; S(mе-1) – накопленная частота интервала, предшествующего медианному; fmе – частота медианного интервала. Мода, медиана, средняя для дискретного ряда распределения и для интервального ряда называются показателями центра распределения, т.к. они используются для анализа вариационных рядов. |
|||||||||||||||||
2. Ряды динамики. Построение характеристик динамических рядов. Прогнозирование в рядах динамики на основе тренда |
Динамическим рядом (рядом динамики) называются ряды изменяющихся во времени значений статистического показателя, расположенных в хронологическом порядке и описывающих процесс развития, движения социально-экономических явлений и процессов во времени. Относящиеся к отдельным периодам или датам значения признака – это уровни динамического ряда (yi), периоды или даты, за которые представлены значения показателя – это показатели времени (ti). Принципы построения цепных и базисных показателей динамики: 1. Базисные показатели: каждый уровень динамического ряда сравнивается с одним и тем же предшествующим уровнем, принятым за базу сравнения. 2. Цепные показатели: каждый уровень динамического ряда сравнивается с непосредственно ему предшествующим, такое сравнение называют иногда сравнением с переменной базой. Абсолютный прирост:
показывает в натуральных измерителях отличие текущего уровня от предшествующего или базисного уровня.
Коэффициент роста и темп роста
показывает, во сколько раз отличается текущий уровень от предшествующего уровня либо базисного. Ti= ki100% (28) Темп прироста
или Ti=(ki-1) 100%=Ti – 100% (30) показывает на сколько процентов изменился текущий уровень по сравнению с предшествующим уровнем либо базисным. Абсолютное значение 1 % прироста (снижения) имеет смысл только для цепных характеристик динамических рядов: i(цепн)
Ti(цепн)(%) показывает в натуральных измерителях, сколько приходится на 1% прироста. Средние величины (за исключением среднего уровня ряда) в рядах динамики рассчитываются на основе соответствующих цепных показателей и показывают общую характеристику изменений в ряду динамики:
Средний
абсолютный прирост Средний коэффициент роста, средний темп роста
Средний темп прироста
Средний уровень ряда в зависимости от вида ряда (моментный или интервальный) и вида временных промежутков (равноотстоящие или не равноотстоящие уровни) рассчитывается по разным формулам. Коэффициент
опережения: сравнивает различные явления во времени. Построение тренда в рядах динамики.
где a – начальный уровень тренда в момент начала отсчета t, b – среднегодовой абсолютный темп прироста,
Система нормальных уравнений для линейного тренда имеет вид:
Значения условных показателей времени задаются с таким условием, чтобы сумма их нечётных степеней равнялась 0. Оценка тренда производится после расчёта параметров тренда, теоретических значений уровней ряда и относительной ошибки тренда:
где
yi – фактические уровни ряда,
n – число уровней ряда, m – число параметров тренда. Точечный прогноз уровня можно построить, подставив в полученное уравнение тренда значение условного показателя времени, соответствующее прогнозируемому уровню. |
3. ПОКАЗАТЕЛИ ВАРИАЦИИ (КОЛЕБЛЕМОСТИ) ПРИЗНАКА |
|
3.1. Абсолютные показатели вариации |
Вариация – это изменение значения признака у отдельных единиц совокупности. Вариация обусловлена действием различных факторов на развитие отдельных единиц совокупности. Чем более разнообразно условие, тем больше его вариация. Наиболее простой характеристикой вариации признака является размах вариации (R). Размах вариации – это разность между наибольшим и наименьшим значением признака в изучаемой совокупности: R=xmax – xmin, где xmax – наибольшее значение признака; xmin – наименьшее значение признака. Размах вариации не отражает отклонений всех значений признака – это его недостаток. Он исчисляется при контроле качества продукции для определения систематически действующих причин на производственный процесс. Для измерения отклонения каждой варианты от средней величины в ряду распределения или в группировке применяется среднее линейное отклонение (d). Среднее линейное отклонение определяется по формулам:
а)
для несгруппированных
данных (ранжировочного
ряда)
б) для
вариационного
интервального ряда: Среднее линейное отклонение показывает, на сколько в среднем каждое значение признака отклоняется от средней величины. Эта величина всегда именованная и измеряется в тех же величинах, в которых даны статистические показатели. Среднее линейное отклонение дает обобщенную характеристику степени колеблемости признаков совокупности. Средние линейные отклонения применяются на практике для анализа состава рабочих, ритмичности производства, равномерности поставок материалов и т.д.
Наибольшее
применение в практике статистических
работ находит показатель – дисперсия
признака или средний квадрат отклонений,
или квадрат среднего квадратического
отклонения (
а)
для ранжировочного ряда (несгруппировочных
данных):
б)
для интервального ряда:
Корень
квадратный из дисперсии
представляет
среднее квадратическое отклонение
(
а)
для
ранжировочного ряда:
б)
для
вариационного ряда: Среднее квадратическое отклонение дает обобщенную характеристику признака совокупности и показывает во сколько раз в среднем колеблется величина признака совокупности. В зарубежной литературе оно называется стандартным отклонением и применяется в различных стандартах. Среднее квадратическое отклонение по величине всегда больше среднего линейного отклонения. Среднее квадратическое отклонение является мерой надежности средней величины: чем оно меньше, тем точнее средняя арифметическая. Дисперсия является оценкой одноименного показателя теории вероятности. Сопоставление линейных или среднеквадратических отклонений по признакам совокупности дает возможность определить статистическую однородность совокупности: чем меньше размер, тем совокупность более однородна. |
3.2. Относительные показатели вариации |
Для сравнения вариации в разных совокупностях рассчитываются относительные показатели вариации. К ним относятся коэффициент вариации, коэффициент осцилляции и линейный коэффициент вариации (относительное линейное отклонение). Коэффициент вариации – это отношение среднеквадратического отклонения к среднеарифметическому, рассчитывается в процентах:
Коэффициент вариации позволяет судить об однородности совокупности: – 17% – абсолютно однородная; – 17–33%% – достаточно однородная; – 35–40%% – недостаточно однородная; – 40–60%% – это говорит о большой колеблемости совокупности.
Коэффициент
осцилляции –
это отношение размаха вариации к
средней, в процентах. Отражает
относительную колеблемость крайних
значений признака вокруг средней.
Линейный
коэффициент
вариации характеризует долю усредненного
значения абсолютного отклонения от
средней величины. |
3.3. Виды дисперсии |
В зависимости от того, как представлена статистическая совокупность одним элементом или несколькими, различают следующие виды дисперсии: – общая дисперсия; – групповая дисперсия (внутригрупповая); – средняя из групповых дисперсия; – межгрупповая дисперсия.
Общая
дисперсия
оценивает колеблемость признака всех
единиц совокупности без исключения:
f – частота в целом по совокупности. Она отражает влияние всех причин и факторов, которые действуют на вариацию.
Для
характеристики вариации признаков
по группе рассчитывают групповую
дисперсию.
Она рассчитывает колеблемость признака
в каждой отдельной группе и представляет
собой средний квадрат отклонений
индивидуальных значений признаков
от средней по каждой отдельно взятой
группе:
Средняя из групповых дисперсия – это среднеарифметическая взвешенная из групповых дисперсий и определяется по формуле
где Межгрупповая дисперсия (дисперсия групповых средних) характеризует вариацию результативного признака под влиянием только одного фактора, положенного в равновесие группировки
где
Отношение
межгрупповой дисперсии к общей
дает коэффициент детерминации:
Если
Если
Между
общей дисперсией, средней из групповых
дисперсий и межгрупповых дисперсий
существует соотношение, которое
определяет правило сложения
дисперсий: Практическое применение правила: используется для взаимопроверки правильности расчета обшей дисперсии, на основании этого правила строятся показатели тесноты связи. |
4. Расчёт экономических индексов в статистике |
|||||||||||||||||||||||||||||||||||||||||||||
В статистике под индексом понимают относительный показатель, который выражает соотношение величин какого-либо явления во времени, пространстве, сравнивает фактические данные с любым эталоном (нормативом, планом, прогнозом и т.д.) Основным элементом индексного соотношения является индексируемая величина. Основные обозначения и символы: p – цена (стоимость) единицы товара (продукции); q – количество (объём) какого-либо продукта (товара) в натуральном выражении; z – себестоимость единицы продукции; t – затраты времени на выработку единицы продукции; pq – стоимость продукции (товарооборот); zq – затраты (издержки) на производство продукции; tq – затраты времени (трудоёмкость) на производство продукции и т.д. индивидуальный
индекс физического объёма – индивидуальный
индекс цены – индивидуальный
индекс себестоимости – индивидуальный
индекс стоимости (товарооборота) – индивидуальный
индекс издержек (затрат) – где Определение: Общий индекс в статистике – относительный показатель, служащий для сравнения сложных явлений и включающий в себя индексируемую величину, состояния которой сравниваются, и вес – показатель, определяющий значимость каждой индексируемой величины. Общие индексы строятся для количественных и качественных показателей. Кроме этого по способу расчёта показатели делятся на агрегатные индексы и средние из индивидуальных. Определение: Агрегатным индексом называется индекс, у которого числитель и знаменатель представляют собой набор непосредственно несоизмеримых и неподдающихся непосредственному суммированию элементов: сумму произведений двух величин, одна из которых меняется (индексируется), а другая (вес индекса) – остаётся неизменной в числителе и знаменателе, служит для соизмерения индексируемых величин. Типичным индексом количественного показателя является индекс физического объёма. Для вычисления этого индекса, являющегося сложным индексом, введём коэффициенты соизмерения, полученные умножением объёма каждого вида продукции (q) на соответствующую цену (p) – pq; себестоимость(z) – zq; затраты времени(t) – tq и т д. Тогда общий индекс физического объёма продукции (товара):
Этот индекс характеризует процесс реализации, а
характеризует процесс производства продукции. Общий индекс стоимости продукции (общий индекс товарооборота):
Для
расчёта общего индекса как среднего
из индивидуальных воспользуемся
индивидуальным индексом физического
объёма, из которого получим значения
недостающих элементов. Так например,
если по имеющейся информации нет
значения
и т.д.
Таблица 5 Основные формулы исчисления общих индексов
Окончание таблицы 5
И так далее. . Общие индексы средних величин Изучение совместного действия факторов на изменение среднего значения качественного признака и изменение структуры явления решается построением системы взаимосвязанных индексов:
1. Индекс
переменного состава показывает изменение среднего значения качественного показателя (средней цены) в текущем периоде по сравнению с базисным или предыдущим.
2. Индекс
постоянного состава показывает изменение среднего значения качественного показателя (средней цены) в зависимости от изменения этого показателя у отдельных единиц совокупности.
3. Индекс
структурных сдвигов показывает изменение среднего значения качественного показателя в зависимости от изменения структурных пропорций. |
Семестр 2
1. Статистика рабочей силы и рабочего времени предприятия
Статистика рабочей силы изучает состав и численность рабочей силы. В сфере материального производства рабочая сила подразделяется на персонал, занятый в основной деятельности предприятия, и персонал неосновной деятельности.
Основная категория персонала – это рабочие.
К категориям численности рабочих и служащих относятся списочная и явочная численность, число фактически работавших. В списочную численность входят все работники предприятия, принятые на срок один и более дней. Явочное число включает работников, явившихся на работу, а также находящихся в командировках и занятых на других предприятиях по нарядам своей организации.
Все категории численности определяются на конкретную дату, но для многих экономических расчетов необходимо знать среднюю численность работников – среднесписочную, среднеявочную и среднюю фактически работавших.
Среднесписочная численность определяется следующими способами.
Допустим, что известна списочная численность на начало и конец периода, тогда среднесписочная численность определяется как полусумма этих величин.
Среднесписочная численность за квартал, полугодие и год определяется как средняя арифметическая из среднемесячных чисел:
![]()
где Т – сумма среднемесячных чисел работников на число месяцев периода. Если известна списочная численность на даты через одинаковые интервалы времени, например на начало или конец каждого месяца, то среднесписочная численность за квартал, полугодие или год находится по формуле средней хронологической:
![]()
где n – число показателей; T 1– численность на первую дату, Т 2, Т 3 – на другие даты
Среднеявочная численность работников определяется по формуле:
![]()
Средняя численность фактически работавших исчисляется формулой:
![]()
Рабочее время измеряется в человеко-днях и человеко-часах.
2. Календарный фонд. Производительность труда
Календарный фонд – это все время отчетного периода, равен произведению числа календарных дней в периоде на списочную численность работников.
Табельный фонд меньше календарного на число праздничных и выходных человеко-дней.
Максимально возможный фонд меньше табельного фонда за счет времени очередных отпусков.
Фактически отработанный фонд времени меньше максимально возможного за счет различных потерь рабочего времени.

![]()
Производительность труда – результативность живого труда, эффективность производительной деятельности по созданию продукта в течение времени.
Через показатели трудоемкости и выработки характеризуется производительность труда.
Выработка (W) продукции в единицу времени измеряется соотношением объема произведенной продукции (q) и затратами (Т) рабочего времени (среднесписочная численность):
![]()
Обратным показателем является трудоемкость:
![]()
Выработка показывает, сколько вырабатывается продукции за единицу рабочего времени.
В зависимости от измерения затрат труда различают следующие уровни производительности.
Средняя часовая выработка = объем произведенной продукции / число человеко-часов, отработанных в течение данного периода.
Средняя дневная выработка = объем произведенной продукции / число человеко-часов, отработанных всеми рабочими предприятия.
Среднемесячная выработка = объем произведенной продукции / среднесписочное число рабочих.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3. Статистика заработной платы |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Заработная плата – показатель, который входит составляющей при расчётах себестоимости, издержек производства. Основным показателем, характеризующим заработную плату, является средняя её величина как для отдельных групп работников, так и для предприятия в целом.
Динамика
средней заработной платы анализируется
с применением индексного метода,
который может быть представлен
следующей системой показателей:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример решения и оформления задачи |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Таблица 14.1 Данные о заработной плате работников предприятия
1. Как изменилась заработная плата по каждому виду персонала (в абсолютных и относительных показателях)? 2. Рассчитать сверхплановую, плановую и фактическую экономию или перерасход ФЗП. 3. Сделайте выводы по результатам выполненной работы. Пример решения и оформления см. в таблице 14.2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Контрольные вопросы |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1. По каким формулам производились расчёты для п.1 задачи? 2. По каким формулам производились расчёты в п.2 задачи? 3. Какие выводы сделали по результатам выполненной работы?
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример оформления и решения задачи |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Таблица 14.2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


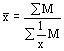
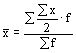 .
. ,
,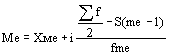 ,
,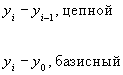 (26)
(26)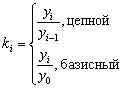 (27)
(27)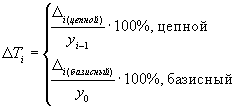 (29)
(29) (33)
(33) (35)
(35)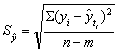 ),
),