3.3. Волновые методы

По мере того как частота электромагнитного поля увеличивается до 10⁹ Гц, длина волны становится сравнимой с размерами образца. Поле внутри образца изменяется от точки к точке, и диэлектрический отклик необходимо анализировать с помощью уравнений Максвелла для электромагнитного поля. Для целей измерения удобно локализовать волну в коаксиальном волноводе, представляющем собой центральный проводник, заключенный в полую проводящую трубку или. при очень высоких частотах, простой волновод прямоугольного или круглого сечения. Диапазон длин волн, в котором может использоваться этот метод, от 1 до 300 мм, обычно называют СВЧ-(сверхвысокочастотным) диапазоном.

Вначале необходимо соотнести основной параметр волны, коэффициент распространения γ* материала, с его диэлектрической проницаемостью. С помощью коэффициента распространения уравнения электрического и магнитного поля волны, распространяющейся вдоль оси х в однородной неограниченной среде, записываются в виде

где соответствующие векторы поля Е и Н ортогональны (поперечная электромагнитная волна, или ТЕМ-волна). Из уравнений Максвелла получаем выражение для комплексного коэффициента распространения среды:

где ε*_S и μ*_S — абсолютные (комплексные) диэлектрическая и магнитная проницаемости среды. Действительная часть α_S определяет затухание (равное нулю в вакууме) волны, а комплексная часть β_S задает длину волны λ_S в среде:

В вакууме выражение для коэффициента распространения принимает более простой вид:

где ε₀ и μ₀— диэлектрическая и магнитная проницаемости свободного пространства, соответственно. Комплексная диэлектрическая проницаемость немагнитной (μ* = μ₀) диэлектрической среды на угловой частоте ω связана с коэффициентом распространения плоской волны той же частоты в среде соотношением

где λ₀ – длина волны той же частоты в вакууме. Приравнивая действительную и мнимую части, имеем

г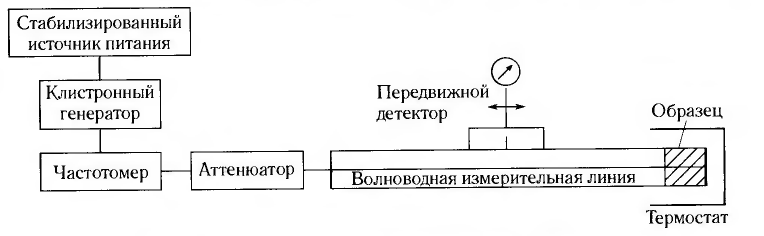 де n — показатель преломления среды на данной частоте.

Рис. 15. Схема волноводной измерительной линии

Рис. 16. Стоячие волны в пустом волноводе (а) и часть волновода перед заглушкой, заполненная диэлектриком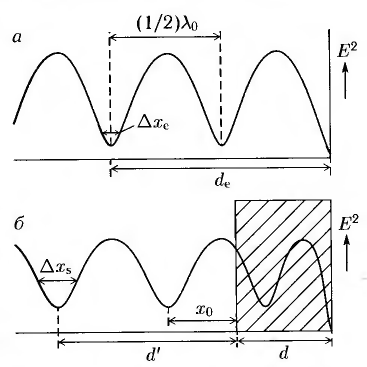

В методе Roberts и von Hippel (1946) диэлектрик заполняет часть волновода или коаксиальной линии длиной d перед заглушкой, как показано на рис. 15. Для жидких образцов волновод должен быть расположен вертикально. Картина возникающих стоячих волн изображена на рис. 16. Волна в пространстве перед образцом характеризуется

а) обратной величиной коэффициента стоячей волны Е_min/Е_max, т.е. отношением амплитуды стоячей волны в узле и пучности,

б) расстоянием х₀ первого узла от поверхности образца,

в) длиной волны λ_0g, равной удвоенному расстоянию между соседними узлами.

Для образцов с малыми потерями обратную величину коэффициента стоячей волны можно очень точно определить, измеряя ширину узла волны:

где Δx — расстояние между точками удвоенной мощности по обеим сторонам от минимума. Для образцов с очень малыми потерями необходимо учитывать потери в стенках линии передачи, которые можно оценить из ширины Δx_e узла на расстоянии d_е от конца пустой линии. Вначале в измеренное значение ширины Δх_S узла на расстоянии d' перед образцом вносится поправка на потери в стенках:

Суммарное значение tgδ для отрезка линии с образцом вычисляют с помощью уравнения

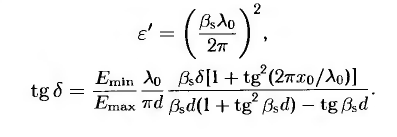
Затем вычитают потери в стенках и получают величину потерь для самого образца.