
Минобрнауки России
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Национальный исследовательский университет Московский энергетический институт»
(ФГБОУ ВПО «НИУ МЭИ»)
Факультет «Институт экономической безопасности бизнеса» (ИЭББ)
Кафедра «Защита информации»
Творческая работа по дисциплине «Теория вероятностей и математическая статистика»
Работу выполнили:
студенты гр. ИБС 11-12
Биктимеров Р.Ш.
Будынков А.Н
Работу проверила:
Кленина Л.И
Оценка______________
Подпись______________
Москва 2013
Оглавление
Введение 3
Группировка статистических данных 4
Характеристики случайной величины 11
Проверка гипотез о виде распределения 12
Проверка гипотез о виде распределения 15
Введение
В данной работе производится статистическая оценка данных, содержащих время доставки абонентам SMS сообщений. В статистическую оценку входит: группировка данных по формуле Стэрджесса, оценка выборочного среднего, дисперсии, моды, медианы, среднеквадратического отклонения случайной величины, которой является время доставки, а также, используя критерий согласия Пирсона, проверка гипотезы о виде распределения случайной величины.
Входными данными являются 200 выборок времени доставки SMS абоненту. Обозначим эту случайную величину за X.
Группировка статистических данных
Собранный в процессе статистического наблюдения материал нуждается в определенной обработке, сведении разрозненных данных воедино.
Научно организованная обработка материалов, включающая в себя кроме обязательного контроля собранных данных систематизацию, группировку материалов, составление таблиц, получение итогов и производных показателей (средних, относительных величин), называется в статистике сводкой.
Сводка представляет собой второй этап статистического исследования. Целью сводки является получение на основе сведенных материалов обобщающих статистических показателей, отражающих сущность социально-экономических явлений и определенные статистические закономерности.
Статистическая сводка осуществляется по программе, которая должна разрабатываться еще до сбора статистических данных, практически одновременно с составлением плана и программы статистического наблюдения. Программа сводки включает определение групп и подгрупп; системы показателей; видов таблиц.
Группировка – это разбиение совокупности на группы, однородные по какому-либо признаку. С точки зрения отдельных единиц совокупности группировка – это объединение отдельных единиц совокупности в группы, однородные по каким-либо признакам.
Метод группировки основывается на следующих категориях – это группировочный признак, интервал группировки и число групп.
Группировочный признак – это признак, по которому происходит объединение отдельных единиц совокупности в однородные группы.
Интервал очерчивает количественные границы групп. Как правило, он представляет собой промежуток между максимальными и минимальными значениями признака в группе.
Определение числа групп.
В данной работе число групп приближенно определяется по формуле Стэрджесса.
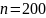

Ширина интервала составит:
 – максимальное значение группировочного
признака в совокупности
– максимальное значение группировочного
признака в совокупности
 – минимальное значение группировочного
признака в совокупности
– минимальное значение группировочного
признака в совокупности
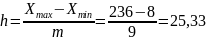
Определим границы группы
Для каждого значения ряда подсчитаем, сколько раз оно попадает в тот или иной интервал. Для этого сортируем ряд по возрастанию.
Значение |
Интервал |
Подсчёт количества |
8 |
8 - 33.33 |
1 |
8 |
8 - 33.33 |
2 |
8 |
8 - 33.33 |
3 |
8 |
8 - 33.33 |
4 |
8 |
8 - 33.33 |
5 |
8 |
8 - 33.33 |
6 |
8 |
8 - 33.33 |
7 |
9 |
8 - 33.33 |
8 |
9 |
8 - 33.33 |
9 |
9 |
8 - 33.33 |
10 |
9 |
8 - 33.33 |
11 |
9 |
8 - 33.33 |
12 |
9 |
8 - 33.33 |
13 |
9 |
8 - 33.33 |
14 |
9 |
8 - 33.33 |
15 |
9 |
8 - 33.33 |
16 |
9 |
8 - 33.33 |
17 |
10 |
8 - 33.33 |
18 |
10 |
8 - 33.33 |
19 |
10 |
8 - 33.33 |
20 |
10 |
8 - 33.33 |
21 |
10 |
8 - 33.33 |
22 |
11 |
8 - 33.33 |
23 |
11 |
8 - 33.33 |
24 |
12 |
8 - 33.33 |
25 |
12 |
8 - 33.33 |
26 |
12 |
8 - 33.33 |
27 |
12 |
8 - 33.33 |
28 |
12 |
8 - 33.33 |
29 |
12 |
8 - 33.33 |
30 |
12 |
8 - 33.33 |
31 |
12 |
8 - 33.33 |
32 |
12 |
8 - 33.33 |
33 |
12 |
8 - 33.33 |
34 |
12 |
8 - 33.33 |
35 |
12 |
8 - 33.33 |
36 |
12 |
8 - 33.33 |
37 |
12 |
8 - 33.33 |
38 |
12 |
8 - 33.33 |
39 |
12 |
8 - 33.33 |
40 |
12 |
8 - 33.33 |
41 |
12 |
8 - 33.33 |
42 |
12 |
8 - 33.33 |
43 |
12 |
8 - 33.33 |
44 |
12 |
8 - 33.33 |
45 |
12 |
8 - 33.33 |
46 |
12 |
8 - 33.33 |
47 |
13 |
8 - 33.33 |
48 |
13 |
8 - 33.33 |
49 |
13 |
8 - 33.33 |
50 |
13 |
8 - 33.33 |
51 |
13 |
8 - 33.33 |
52 |
13 |
8 - 33.33 |
53 |
14 |
8 - 33.33 |
54 |
14 |
8 - 33.33 |
55 |
14 |
8 - 33.33 |
56 |
14 |
8 - 33.33 |
57 |
14 |
8 - 33.33 |
58 |
14 |
8 - 33.33 |
59 |
14 |
8 - 33.33 |
60 |
14 |
8 - 33.33 |
61 |
15 |
8 - 33.33 |
62 |
15 |
8 - 33.33 |
63 |
15 |
8 - 33.33 |
64 |
17 |
8 - 33.33 |
65 |
18 |
8 - 33.33 |
66 |
18 |
8 - 33.33 |
67 |
18 |
8 - 33.33 |
68 |
18 |
8 - 33.33 |
69 |
18 |
8 - 33.33 |
70 |
18 |
8 - 33.33 |
71 |
18 |
8 - 33.33 |
72 |
18 |
8 - 33.33 |
73 |
18 |
8 - 33.33 |
74 |
18 |
8 - 33.33 |
75 |
18 |
8 - 33.33 |
76 |
18 |
8 - 33.33 |
77 |
18 |
8 - 33.33 |
78 |
18 |
8 - 33.33 |
79 |
18 |
8 - 33.33 |
80 |
18 |
8 - 33.33 |
81 |
18 |
8 - 33.33 |
82 |
18 |
8 - 33.33 |
83 |
19 |
8 - 33.33 |
84 |
19 |
8 - 33.33 |
85 |
19 |
8 - 33.33 |
86 |
19 |
8 - 33.33 |
87 |
19 |
8 - 33.33 |
88 |
19 |
8 - 33.33 |
89 |
19 |
8 - 33.33 |
90 |
19 |
8 - 33.33 |
91 |
19 |
8 - 33.33 |
92 |
19 |
8 - 33.33 |
93 |
19 |
8 - 33.33 |
94 |
19 |
8 - 33.33 |
95 |
19 |
8 - 33.33 |
96 |
19 |
8 - 33.33 |
97 |
19 |
8 - 33.33 |
98 |
19 |
8 - 33.33 |
99 |
19 |
8 - 33.33 |
100 |
19 |
8 - 33.33 |
101 |
19 |
8 - 33.33 |
102 |
19 |
8 - 33.33 |
103 |
19 |
8 - 33.33 |
104 |
19 |
8 - 33.33 |
105 |
19 |
8 - 33.33 |
106 |
19 |
8 - 33.33 |
107 |
19 |
8 - 33.33 |
108 |
19 |
8 - 33.33 |
109 |
19 |
8 - 33.33 |
110 |
19 |
8 - 33.33 |
111 |
19 |
8 - 33.33 |
112 |
19 |
8 - 33.33 |
113 |
19 |
8 - 33.33 |
114 |
19 |
8 - 33.33 |
115 |
19 |
8 - 33.33 |
116 |
19 |
8 - 33.33 |
117 |
19 |
8 - 33.33 |
118 |
19 |
8 - 33.33 |
119 |
19 |
8 - 33.33 |
120 |
19 |
8 - 33.33 |
121 |
19 |
8 - 33.33 |
122 |
19 |
8 - 33.33 |
123 |
19 |
8 - 33.33 |
124 |
19 |
8 - 33.33 |
125 |
20 |
8 - 33.33 |
126 |
20 |
8 - 33.33 |
127 |
20 |
8 - 33.33 |
128 |
20 |
8 - 33.33 |
129 |
20 |
8 - 33.33 |
130 |
20 |
8 - 33.33 |
131 |
20 |
8 - 33.33 |
132 |
20 |
8 - 33.33 |
133 |
20 |
8 - 33.33 |
134 |
20 |
8 - 33.33 |
135 |
20 |
8 - 33.33 |
136 |
20 |
8 - 33.33 |
137 |
20 |
8 - 33.33 |
138 |
20 |
8 - 33.33 |
139 |
20 |
8 - 33.33 |
140 |
22 |
8 - 33.33 |
141 |
24 |
8 - 33.33 |
142 |
24 |
8 - 33.33 |
143 |
24 |
8 - 33.33 |
144 |
24 |
8 - 33.33 |
145 |
24 |
8 - 33.33 |
146 |
24 |
8 - 33.33 |
147 |
24 |
8 - 33.33 |
148 |
27 |
8 - 33.33 |
149 |
33 |
8 - 33.33 |
150 |
63 |
58.66 - 83.99 |
1 |
71 |
58.66 - 83.99 |
2 |
71 |
58.66 - 83.99 |
3 |
72 |
58.66 - 83.99 |
4 |
72 |
58.66 - 83.99 |
5 |
73 |
58.66 - 83.99 |
6 |
74 |
58.66 - 83.99 |
7 |
87 |
83.99 - 109.32 |
1 |
90 |
83.99 - 109.32 |
2 |
90 |
83.99 - 109.32 |
3 |
90 |
83.99 - 109.32 |
4 |
91 |
83.99 - 109.32 |
5 |
92 |
83.99 - 109.32 |
6 |
92 |
83.99 - 109.32 |
7 |
92 |
83.99 - 109.32 |
8 |
92 |
83.99 - 109.32 |
9 |
92 |
83.99 - 109.32 |
10 |
92 |
83.99 - 109.32 |
11 |
93 |
83.99 - 109.32 |
12 |
93 |
83.99 - 109.32 |
13 |
93 |
83.99 - 109.32 |
14 |
93 |
83.99 - 109.32 |
15 |
94 |
83.99 - 109.32 |
16 |
94 |
83.99 - 109.32 |
17 |
94 |
83.99 - 109.32 |
18 |
95 |
83.99 - 109.32 |
19 |
96 |
83.99 - 109.32 |
20 |
96 |
83.99 - 109.32 |
21 |
97 |
83.99 - 109.32 |
22 |
97 |
83.99 - 109.32 |
23 |
97 |
83.99 - 109.32 |
24 |
97 |
83.99 - 109.32 |
25 |
97 |
83.99 - 109.32 |
26 |
97 |
83.99 - 109.32 |
27 |
98 |
83.99 - 109.32 |
28 |
98 |
83.99 - 109.32 |
29 |
99 |
83.99 - 109.32 |
30 |
99 |
83.99 - 109.32 |
31 |
99 |
83.99 - 109.32 |
32 |
99 |
83.99 - 109.32 |
33 |
100 |
83.99 - 109.32 |
34 |
100 |
83.99 - 109.32 |
35 |
102 |
83.99 - 109.32 |
36 |
106 |
83.99 - 109.32 |
37 |
106 |
83.99 - 109.32 |
38 |
109 |
83.99 - 109.32 |
39 |
111 |
109.32 - 134.65 |
1 |
128 |
109.32 - 134.65 |
2 |
236 |
210.64 - 236 |
1 |
236 |
210.64 - 236 |
2 |
Одно и то же значение признака служит верхней и нижней границами двух смежных (предыдущей и последующей) групп.
Результаты группировки оформим в виде таблицы:
Группы |
Частота fi |
8 - 33.33 |
150 |
33.33 - 58.66 |
0 |
58.66 - 83.99 |
7 |
83.99 - 109.32 |
39 |
109.32 - 134.65 |
2 |
134.65 - 159.98 |
0 |
159.98 - 185.31 |
0 |
185.31 - 210.64 |
0 |
210.64 - 235.97 |
2 |
Таблица для расчета показателей.
Группы |
Середина интервала,
|
Количество, fi |
* fi |
Накопленная частота, Si |
( |
( - )2 * fi |
Частота, fi/n |
8 - 33.33 |
20.67 |
150 |
3099.75 |
150 |
2944.61 |
57804.95 |
0.75 |
33.33 - 58.66 |
46 |
0 |
0 |
150 |
0 |
0 |
0 |
58.66 - 83.99 |
71.33 |
7 |
499.28 |
157 |
217.2 |
6739.7 |
0.035 |
83.99 - 109.32 |
96.66 |
39 |
3769.55 |
196 |
2198.01 |
123878.24 |
0.2 |
109.32 - 134.65 |
121.99 |
2 |
243.97 |
198 |
163.38 |
13346.27 |
0.01 |
134.65 - 159.98 |
147.32 |
0 |
0 |
198 |
0 |
0 |
0 |
159.98 - 185.31 |
172.65 |
0 |
0 |
198 |
0 |
0 |
0 |
185.31 - 210.64 |
197.98 |
0 |
0 |
198 |
0 |
0 |
0 |
210.64 - 235.97 |
223.31 |
2 |
446.61 |
200 |
366.02 |
66984.77 |
0.01 |
Сумма |
|
200 |
8059.15 |
|
5889.23 |
268753.93 |
1 |
Гистограмма
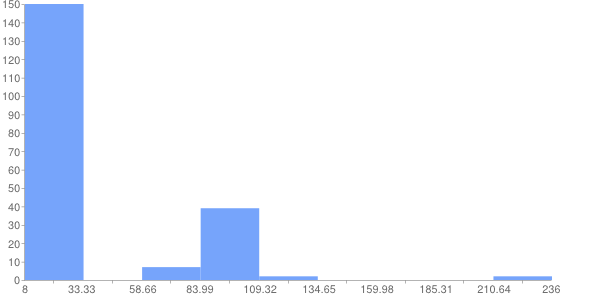
Полигон
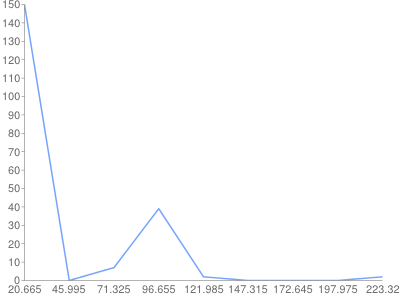

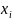
 -
-
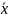 )
* fi
)
* fi