Оглавление

Выбор варианта балочной клетки …………………………………………………..2

Подбор сечения главной балки………………………………………………………4

Изменение сечения балки по длине ………………………………………………..7

Проверка прочности, прогиба и устойчивости сварной балки ……………….7

Проверка и обеспечение местной устойчивости элементов балки …………...8

Соединение поясов балки со стеной ………………………………………………..10

Расчет опорного ребра ………………………………………………………………...10

Расчет и конструирование сплошной колонны …………………………………….11

База колонны …………………………………………………………………………….12

Расчет оголовка сплошной колонны ………………………………………………….13

Литература ……………………………………………………………………………….15

Выбор варианта балочной клетки

Требуется запроектировать конструкцию балочной площадки размером 45х36 м с ж/б настилом и размером ячейки 15х12 м. Дано: временная нормативная, равномерно распределённая по площади нагрузка рн=18,1 кН/см², коэффициент перегрузки п=1,2, материал - ВСтЗкп2, имеющая R=225 МПа=22,5 кН/см², коэффициент условий работы у=1, предельные прогибы балок [f/l]<l/250.

Рассмотрим 2 варианта компоновки балочной площадки: 1- нормальный тип и 2- усложнённый тип

Вариант 1.

Пролёт главной балки делим на 5 равных частей по 300 см - расстояние между балками настила. Фактический пролёт настила — расстояние между краями полок соседних балок — меньше 300 см. Определяем вес настила, зная, что 1м² ж/б настила толщиной 10 см весит 200 кг:

g_H= 2 кН/м².

Нормативная нагрузка на балку настила:

q_H= (p_H+g_H)a = (18,1+2)*3= 60,3 кН/м = 0,60 кН/см

Расчётная нагрузка на балку настила

q= (п_Ррн+nggn)a = (1,2*18,1+1,05*2)*3 = 71,46 кН/м

Расчётный изгибающий момент (длина балки настила 12 м)

М_max=ql²/8= 71,46*12²/8= 1280 кН*м=128000 кН*см

Требуемый момент сопротивления балки определяем, первоначально принимая с,=с=1,1

Wht.tp= Мmax/c₁Rγ=128000/ 1,1*22,5*1= 5170 см³

Принимаем двутавр №40К9а по ТУ 14-2-24-72 8239-72, имеющий: I= 130890см⁴, W= 6030 см³, вес g= 308 кг/м, ширину полки b=43,4 см.

Проверяем только прогиб, так как W= 6030 cm³>Wht.tp:

f=5*0,6*1200⁴/384*2,06*10⁴*130890= 4,9 см < 5 см = (1/250)l

Принятое сечение балки удовлетворяет условиям прочности и прогиба. Проверку касательных напряжений в прокатных балках при отсутствии ослабления опорных сечений обычно не производят, так как она легко удовлетворяется из-за относительно большой толщины стенок балок.

Общую устойчивость балок настила проверять не надо, так как их сжатые пояса надёжно закреплены в горизонтальном направлении приваренным к ним настилом.

Определяем расход материала на 1м² перекрытия: настил = 200кг/м²,

балки настила g/a= 308/3=102,7 кг/м².

Весь расход материала составит 200+102,7=302,7 кг/м²=3,03 кН/м². 1 плита стоит 3400 руб. Следовательно: 40*3400=136000 руб.

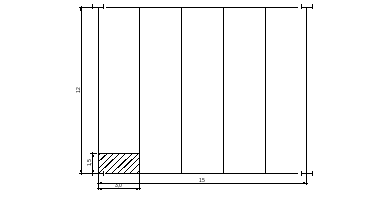
Вариант 2.

Настил принимаем таким же как в первом варианте, расстояние между балками настила

=6 Пролёт балки настила 3м, нормативная и расчётная нагрузки на неё:

q_H= (18.1+2)*6= 120,6 кН/м= 1,2 кН/см;

q= (1,2* 18.1+1,05*2)*6= 142,9 кН/м.

Расчётный изгибающий момент и требуемый момент сопротивления балки:

М= 142,9*3² / 8= 160 кН*м= 16000 кН*см;

Wrp= 16000 / 1,1*22,5= 646 см³.

Принимаем двутавр по ГОСТ 8239-72 №45, имеющий: 1= 27696 см⁴, W= 1231 см³, g= 65,5 кг/м.

Проверяем прогиб балки, так как прочность удовлетворяется выбором W= 743 cm³>Wht.tp:

f=5*1,2*300⁴ / 384*2,06*10⁴*27696= 2,2<2,5 см = (1/250)l.

Принятое сечение удовлетворяет условиям прочности и прогиба. Нагрузку на вспомогательную балку от балок настила считаем сосредоточенной, так как число балок настила < 5. Определяем нормативную и расчётную нагрузку на неё:

q_H= (18.1+2+0,655/ 6)*3= 60 кН/м = 0,6 кН/см;

q= [1,2*18,1+1,05(2+0,655 / 6)]*3= 72кН/м

Определяем расчетный изгибающий момент :

М=72*12²/8= 1296 кН*м =129600кН*см

W_тр=129600/1,1*22,5 = 5236 см³

Принимаем двутавр по ТУ 14-2-24-72 №40К9, имеющий I=130890 см⁴ , W= 6030 см³, ширину и толщину полки Ь= 41,2 см, t= 3,7 см.Исходя из того, что прочность удовлетворяет требуемым условиям(W>Wtp), проверяем балку на прогиб

ƒ= 5*06*1200⁴ / 384*2,06* 10⁴*130890= 4,9 см<3.2 см 1 (1/250)l.

Затем проверяем общую устойчивость вспомогательных балок в середине пролёта, в сечении с наибольшими нормальными напряжениями. Их сжатый пояс закреплён от поперечных смещений балками настила, которые вместе с приваренным к ним настилом образуют жёсткий диск. В этом случае за расчётный пролёт следует принимать расстояние между балками настила 1о= 72.0 см.

l<h/b= 1,05<6; b/t= 19/1.78= 10.67<35 в сечении l/2; при т=0 и Ci=C получаем δ= 0,3

Подставляя значения δ, получаем:

1о/Ь= 8 [0,41 +0,0032b/t+(0,73-0,016b/t)b/h] 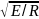= 0,3 [0,41 +0,0032*41,2/3,7+(0,73- 0,016*41,2/3,7)]* = 12,3

Поскольку 12,3>11,73 принятое сечение удовлетворяет требованиям прочности, устойчивости и прогиба.

Расчет металла: по варианту 2 суммарный расход материала

((200+65,5/6)+(308/3))=3,13 кг/м².

Определяем стоимость второго варианта:1 плита 7000руб. Следовательно: 20*7000=140000руб

По расходу материала вариант 1 выгоднее., и она более дешевле по стоимости.

Подбор сечения главной балки

Требуется подобрать сечение сварной главной балки, имеющий прогиб f<(l/400)I из стали ВСтЗ, толщиной t<20MM. Она имеет R=230 МПа =23кН/см² и Rcp=135 Mn a=13,5 кН/см², вес настила и балок настила g= 3,03 кН/м². Собственный вес балки принимаем ориентировочно в размере 1-2% от нагрузки на неё. Максимально возможная строительная высота перекрытия 1,5 м. Определяем нормативную и расчётную нагрузки на балку:

q^H=p^H+g^H= 1,02(18.1+3,03)*12= 258 кН/м

q= п_pр^н+п_gg^н= 1,02(1,2* 18,1+1,05*3,03)*12= 304 кН/м

Определяем расчётный изгибающий момент в середине пролёта

М= ql²/8= 304*15²/8= 8550кН*м= 855000кН*см

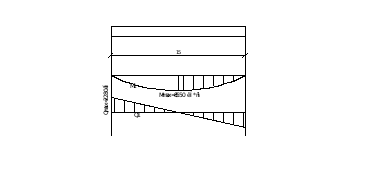
Поперечную силу на опоре:

Q= gl/2= 304* 15 / 2= 2280 кН

Главную балку рассчитываем с учётом развития пластических деформаций. Определяем требуемый момент сопротивления балки:

WTp=Mmax/c₁Rγ= 855000/1,1*23*1=33794 см³

Определяем оптимальную высоту балки, предварительно задав её высоту h=( 1/10)1=1,5 м и рассчитав толщину стенки

tc₁= 7+3h / 1000= 7+3*1500/1000= 11,5 мм.

Принимаем толщину стенки 12 мм.

h_опт= k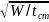 = 1,15 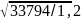= 192 см.

Полученные высота и толщина стенки находятся в пределах, рекомендованных табл.7.2

Минимальную высоту определяем по формуле: 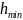=5c₁Rl/24E[l/f](p^H+g^H/n_Pp^H+n_gg^H)=5*l,1*23*1500*400*258/24*2,06*10⁴*304=131 см

Строительную высоту балки определяем исходя из максимально возможной высоты перекрытия и его конструкции

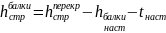=240 – 43,4 — 10 = 187 см

Сравнивая полученные высоты, принимаем высоту балки, близкую к оптимальной 187 см.

Проверяем принятую толщину стенки:

tcr= 7+3*1870/1000= 12.5 мм;

из условия работы стенки на касательные напряжения на опоре:

b_ст= 3*Q_max/2*h*Rcp= 3*2280 / 2*187*13,5= 1,35 см

Чтобы не применять продольных рёбер жёсткости:

t_ст>(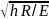 )/5,5>(187 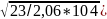/ 5,5= 1,13 см.

Сравнивая расчётным путём толщину стенки с принятой, приходим к выводу, что она удовлетворяет условию прочности на действие касательных напряжений и не требует укрепления её продольным ребром жёсткости для обеспечения местной устойчивости. Размеры горизонтальных поясных листов находим исходя из необходимой несущей способности балки. Для этого вычисляем требуемый момент инерции сечения балки

I=Wh/2= 33794*187/2= 3153739 см⁴

Находим момент инерции стенки балки, принимая толщину поясов 2 см:

h_ст= h - 2tn= 187–2*2= 183 см;

I_ст=t_cтh_ст³/12= 1,2*183³ / 12= 612849 см⁴

Момент инерции, приходящийся на поясные листы:

I_n=I-I_ст =2546890 см⁴

Момент инерции поясных листов балки относительно её нейтральной оси I_n=2A_n(h_o/2)², где А_п- площадь сечения пояса. Моментом инерции поясов относительно их собственной оси ввиду его малости пренебрегаем.

Отсюда получаем требуемую площадь сечения поясов балки

А_п= 2*I_n/h_o²= 2*2546890 / 185²= 149 см², гдеh_o= h - t_n= 187 - 2= 185 см.

Принимаем пояса из универсальной стали 750*20 мм, для которой b_n/h= 750/1870 находится в пределах рекомендуемого отношения. Уточняем принятый ранее коэффициент учёта пластической работы с исходя из

А_п= b_nt_n= 75*2= 150 cm²; А_ст= h_cтt_cт= 1183*1,2= 220 см²;

A_n /А_ст= 150 /220=0.68

По прил. 5 принимаем с=1,088.

Проверяем принятую ширину (свес) поясов, исходя из местной устойчивости: h_св / t_n= 75-1,2/2*2= 14,45<0,ll*h_o/ 0,11*185/1,2= 14,5<0,5 = 15

Проверяем несущую способность балки исходя из устойчивости стенки в области пластических деформаций в месте действия максимального момента, где Q и т=0

λ_ct=(183/1,2) 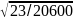= 5,09

M_max= 855000<Ry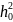 t_CT[(A_n/А_ст)+о]= 23*1*185²*1,2[0,68+0,22]= 866343 кН*см

где а= 0,24 - 0,15(τ/Rc_P)²- 8,5*10^_3(λ_ст- 2,2)²= 0,24 - 8,5*10^_3(5,09 - 2,2)² =0,22

Подобранное сечение балки проверяем на прочность. Для этого определяем момент инерции и момент сопротивления балки

I= I_ст+I_n=I_cт+2b_nt_n(h_o/2)²= 612849+2*75*2(185/ 2)²= 5746596см⁴;

W= I / 0,5*h= 5746596/ 0,5*187= 61460 см³.

Наибольшее нормальное напряжение в балке:

= М_max/ c₁*W= 855000 / 1,1*61460= 21,3 кН/см^2З кН/см²

Подобранное сечение балки удовлетворяет проверке прочности и не имеет недонапряжения больше 5%. Проверку прогиба балки делать не нужно, так как принятая высота сечения больше минимальной и регламентированный прогиб будет обеспечен.

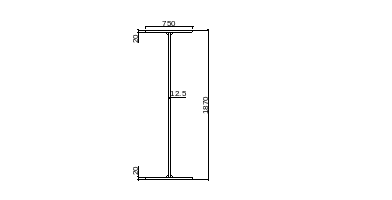
Изменение сечения балки по длине

Требуется изменить сечение сварной балки по длине. Место изменения сечения принимаем на расстоянии 1/6 пролёта от опоры (рис. 5). Сечение изменяем уменьшением ширины поясов. Разные сечения поясов соединяем сварным швом встык электродами Э42 без применения физических методов контроля, т.е. длярастянутого поясаRcb= 0,85R.Определяем расчётный момент и перерезывающую силу в сечении:

X= l/6= 15/6= 2,5 м;

Mi= [qx(l-X)]/2= [304*2,5(15-2,5)]/2= 4750кН*м= 4750000 кН*см;

Qi= q(l/2-x)= 304(15/2 – 2,5)= 1520 кН.

Подбор изменённого сечения ведём по упругой стадии работы материала.

Определяем требуемый момент сопротивления и момент инерции изменённого сечения исходя из прочности сварного стыкового шва, работающего на растяжение:

W₁= M₁ / R_cb= 475000/ 0.85*23= 24295 см³;

I₁= W₁*h / 2= 24295*187 / 2= 2271580 см⁴.

Определяем требуемый момент инерции поясов

(I_ст= 612849 см)

I_n= I₁ - I_ст= 2271580-612849= 1658730 см⁴.

Требуемая площадь сечения поясов

A_n1= 2*I_n1 /h_o1²=2*1658730 / 185²= 96 см².

Принимаем пояс 480*20 мм,. Принятый пояс удовлетворяет рекомендациям b_n1>18 см и b_n1>h/10= 15 см. Определяем момент инерции и момент сопротивления уменьшенного сечения:

I₁=I_ст-2b₁t_n(h/2)²= 612849+2* 48* 2(185/2)²= 2255649см⁴; W₁=2I₁/ h=2*2255649 / 187= 24124 см³;

_max=M_i /W₁= 475000 /24124= 19,48 кН/см² < R^св= 0,85*23= 19,58кН/см².

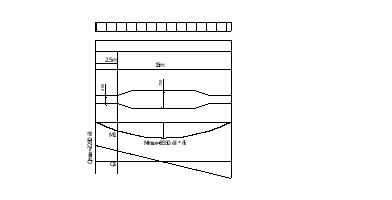
Проверка прочности, прогиба и устойчивости сварной балки

Требуется проверить прочность, общую устойчивость и прогиб сварной балки.

1. Проверка прочности балки. Проверяем максимальные нормальные напряжения в поясах в середине балки:

о=Мmax/c₁*W= 855000 / 1,1*61460= 22,3 kH/cm*<23 кН/см²

Проверяем максимальные касательные напряжения в стенке на опоре балки:

δ=QmaxSi/I₁t_c1= 2280*8907 / 2255649*1,2= 7,5 кН/см²<13,5кН/см²

статический момент полусечения балки Si= b₁t_nh_o/ 2+t_cth²_ct/ 8= 48*2*185 / 2+1*183² / 8= 8907см³. Проверяем местные напряжения в стенке под балками настила:

_м=F /t_ct=857/1,2*45,2= 15,8 kH/cm² <R

где F= 2*71,46*12 / 2= 857кН- опорные реакции балок настила;

l_n=b+2t_n= 41,2+2*2= 45,2 см- длина передачи нагрузки на стенку балки.

Ввиду наличия местных напряжений, действующих на стенку балки, надо проверять совместное действие нормальных, касательных и местных напряжений на уровне поясного шва под балкой настила по уменьшенному сечению вблизи места изменения сечения пояса. В рассматриваемом примере такого места нет, так как под ближайшей балкой настила будет стоять ребро жёсткости, которое воспримет давление балок настила, и передачи давления на стенку в этом месте не будет. Поэтому проверяем приведённые напряжения в сечении 1-1 - месте изменения сечения балки (где они будут максимальны):

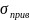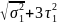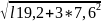= = = 23,2 kH/cm²<1,15R= 26,45 кН/см²

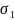= M₁*h_ст/ W₁*h= 475000*183 / 24124*187= 19,2 кН/см²;

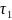= Q₁*S_n1 / I₁*t_cT=1520*8880 / 2255649*1,2= 7,6 кН/см²

S_n1=b₁*t_n*(h_o/ 2)=48*2*185 / 2= 8880см³

Проверки показали, что прочность балки обеспечена.

Проверяем общую устойчивость балки

в месте действия максимальных нормальных напряжений, принимая за расчётный пролёт l₀- расстояние между балками настила:

в середине пролёта балки, где учтены пластические деформации, проверяем применимость формулы: l<h/b_n= 187/75= 2,49<6

l_o/ b_n=300/75= 426 <[0,41+0,0032b_n / t_n + (0,73 - 0,016b_n / t_n)b_n / h_o]* = 0,3[0,41+0,0032*75 / 2 +(0,73- 0,016*75/ 2 )75/ 185]* = 5,23

l_o/b₁=300/48=6,25<1[0,41+0,0032*48/2+(0,73-0,016*48/2)48/185]* =17,2

Обе проверки показали, что общая устойчивость балки обеспечена.

Проверка прогиба

(второе предельное состояние) может не производиться, так как принятая высота балки больше минимальной h= 187 см > h_min=131 см