5) Нормировочное уравнение. Вид. Где используется?

Можно доказать, что, если число состояний системы конечно и из каждого состояния можно перейти (за то или иное число шагов) в любое другое, то существуют предельные (финальные) вероятности состояний, которые не зависят от времени и начального состояния системы. Сумма предельных вероятностей всех состояний системы равна единице:

Это т.н. нормировочное уравнение.

//взято с инета

Пользуясь правилом построения дифференциальных уравнений на основе размеченного графа состояний, записываем систему дифференциальных уравнений относительно вероятностей нахождения СМО в состоянии.

Это соотношение при решении системы дифференциальных уравнений выполняет роль нормировочного уравнения.

//взято с инета

В-3. Непрерывно - стохастические модели.

1) Непрерывно - стохастические модели. Определение

Модели, при моделировании систем и процессов которых используются в качестве типовых математических схем системы СМО (Q-схемы). Такие Q- схемы применяются при формализации процессов функционирования систем, которые по своей сути являются процессами обслуживания.

2) Системы массового обслуживания (смо). Определение. Цель использования. Типы.

Системы массового обслуживания - класс математических схем, разработанных в теории массового обслуживания и различных приложениях для формализации процессов функционирования систем.

Целью исследования является рациональный выбор структуры системы обслуживания и процесса обслуживания на основе изучения потоков требований на обслуживание, поступающих в систему и выходящие из неё, длительности ожидания и длины очередей.

СМО вообще могут быть двух типов.

1.СМО с отказами. В таких системах заявка, поступившая в момент, когда все каналы заняты, получает отказ и покидает систему не обслуженной.

2.СМО с ожиданием. Заявка, заставшая все каналы занятыми, становится в очередь и ожидает освобождения одного из каналов.

3) Задачи теории массового обслуживания.

Задачей теории массового обслуживания является изучение и математическое описание случайного процесса для предоставления рекомендации по рациональной организации этого процесса и предъявить разумные требования к СМО.

4) Понятие потока событий. Чем характеризуются поток требований и поток обслуживания.

A/B/s/m/k

Поток событий - последовательность событий, происходящих одно за другим в некоторые моменты времени.

Поток требований (A) (входной поток) - множество моментов времени поступления в систему заявок;

Поток обслуживаний (B) - множество моментов времени окончания обработки системой заявок в предположении, что обслуживание осуществляется непрерывно.

A и B характеризуют соответственно: поток требований и поток обслуживания, задавая функцию распределения интервалов между заявками во входном потоке и функцию распределения времен обслуживания.

5) Общий вид структуры смо.

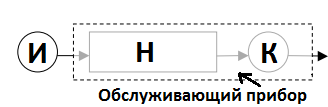
Рис. СМО общего вида

И – источник заявок;

Н – накопитель (очередь);

К – канал обслуживания.

В-4. Непрерывно - стохастические модели.