Лекция № 6 Ряд и интеграл Фурье в анализе нелинейных сау

Функции вида

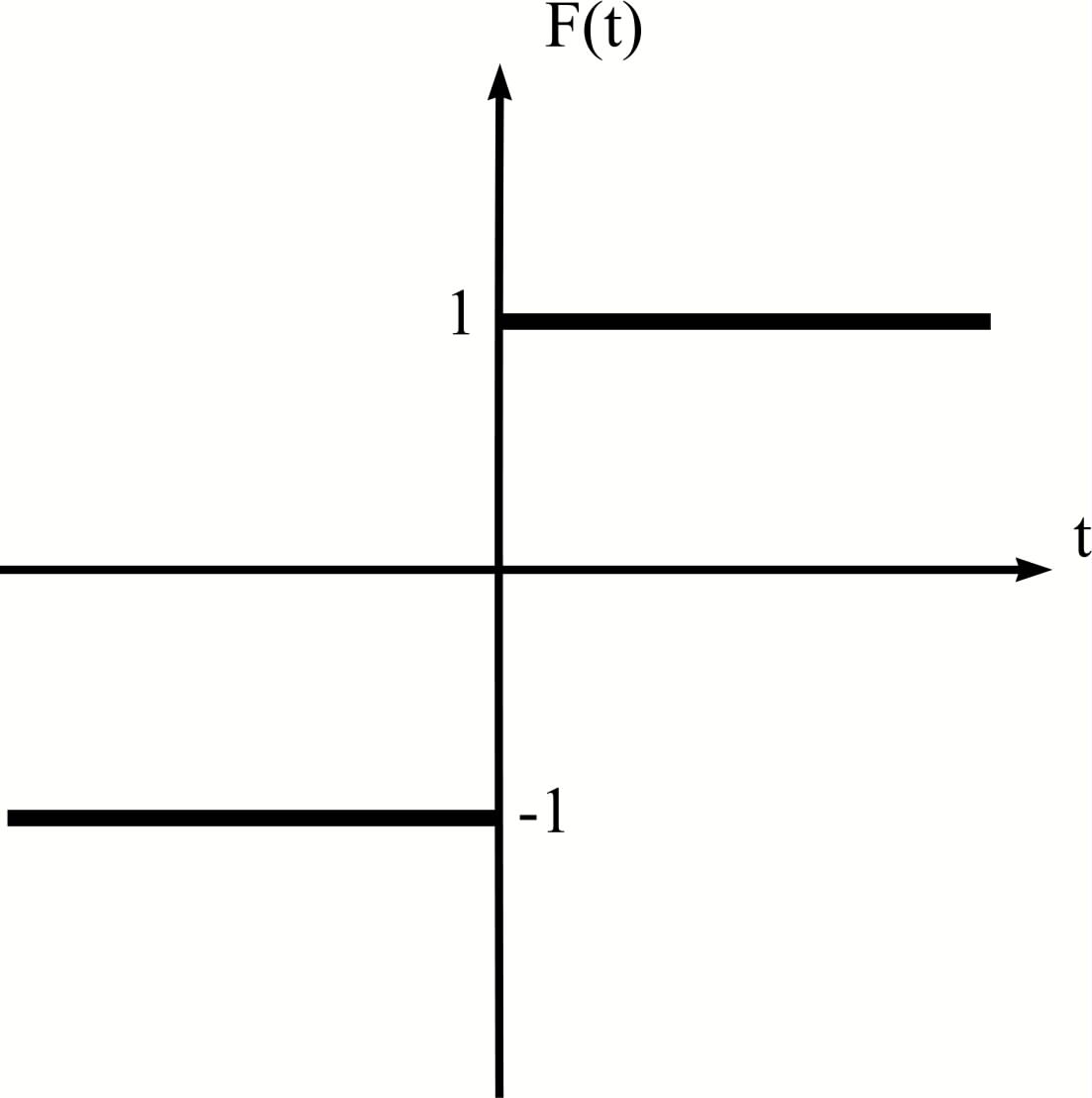
Рис. 6.1. Нелинейная функция

-1 при -  < t < 0

F(t) =

1 при 0 < t < 

неудобны при аналитических исследованиях нелинейных систем управ­ления.

Для облегчения исследовательских задач Фурье предложил такие функции раскладывать в ряд

_n

Fn(t) = a₀ +  [a_kcos(kt) + b_ksin(kt)], где

^k=1

n = 1,2,3,... выбирается в зависимости от желаемой точности апп­роксимации исходной функции F(t);

;

;

;

здесь - частота имеющая размерность - [рад/сек].

Следует заметить, что при n   Fn(t)  F(t), то есть

_

F_n(t) = a₀ +  [a_kcos(kt) + b_ksin(kt)]

^{k = 1}

или в комплексной форме

_

F_n(t) =  c_ke ^(jkt),

^{k = }

_T

где c_k = [ F(t)e^(jkt)dt]/T.

⁰

Пример 1

-1 при -  < t < 0

F(t) ={

1 при 0 < t < 

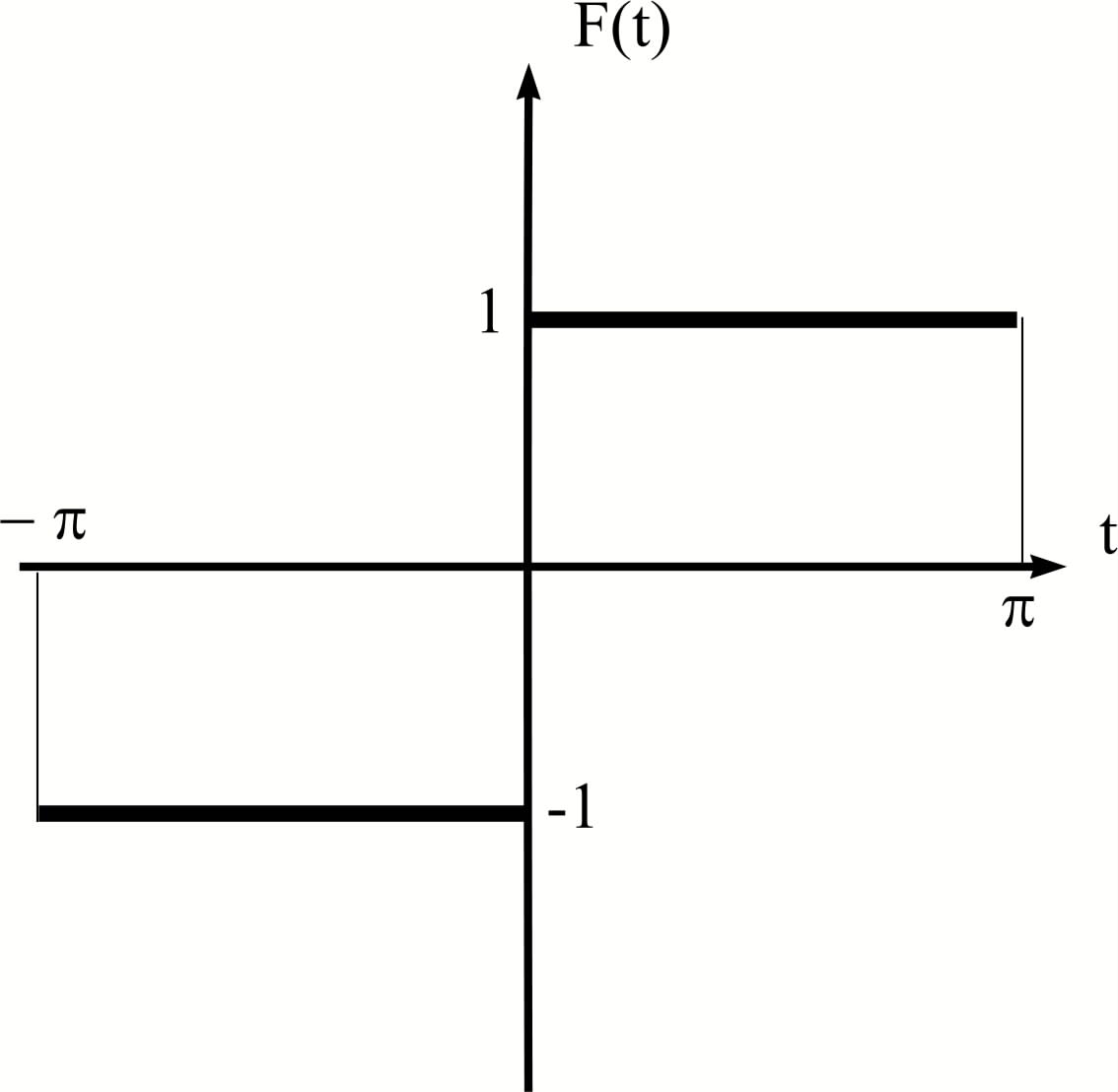
Рис. 6.2. Нелинейная функция с ограничением по времени

Здесь T = 2, a  = 2/T = 1 и

_{0 }

a₀ = [ (-1)dt +  (1)dt]/T = 0;

^{- 0}

_{0 }

a_k = [ (-1)cos(kt)dt +  (1)cos(kt)dt]/ =

^{- 0}

_{0 }

= {-[sin(kt)/k] + [sin(kt)/k]}/ = 0;

^- ⁰

_{0 }

b_k = [ (-1)sin(kt)dt +  (1)sin(kt)dt]/ =

^{- 0}

_{0 }

= {-[-cos(kt)/k] + [-cos(kt)/k]}/ =

^{- 0}

= -[-cos(k0)/k + cos(-k)/k] + [-cos(k)/k + cos(k0)/k]/ =

= 1/k - cos(k)/k - cos(k)/k + 1/k =

= 2[1 - cos(k)]/[k]. При k=1 b₁=4/.

Из последнего выражения следует, что все коэффициенты b_k с четными индексами равны нулю, а с нечетными - 4/[k]. Тогда для k = 1, 2, 3, ...

F_n(t) = 4{sin(1t)/1 + sin(3t)/3 + ... + sin[(2n + 1) t]/[2n + 1],

где n = 0,1,2,3,...,k.

Функцию F_n(t) можно считать аналитической приближенно отражающей функцию F(t).

Более точное приближение получается, если дискретность частот гармонических составляющих стремится к нулю, а число гармоник к бесконеч­ности.

_

F_n(t) = F(t) =  [a()cos(t) + b()sin(t)]d, (6.1)

⁰

_

где a() = [ F(t)cos(t)dt]/;

^

_

b() = [ F(t)sin(t)dt]/.

^

Поскольку, F(t), как следует из выражения (6.1), представляет со­бой сумму бесконечного числа колебаний с амплитудами, зависящими от частоты

A() = [a²() + b²()]^1/2

и фазами

f() = arctg[b()/a()].

Выражение (6.1) можно представить следующим образом

_

F(t) =  A()cos[t - f()]d/.

⁰

При рассмотрении функции F(t) в пределах от -  до  в силу сим­метрии косинуса выражение (6.1) принимает вид

_{ }

F(t) = [ {  F(q)cos[ (t - q)]dq}d]/[2]

^{ }

или в комплексной форме

_

F(t) =  A()e ^{j[t-Q()]}d/2;

^

_{ }

F(t) = [ {  F(q)e ^{ (t - q)} dq}d]/[2]

^{ }

Интеграл Фурье дает разложение временной функции F(t) в непрерыв­ный спектр, тогда как ряды Фурье - в дискретный с частотами  = 2, 4, 6 и т.д.

Плотность спектра (спектральная плотность) характеризуется зави­симостью

_

S() = [ F(t)e ^-jt dt]/[2].

^

Тогда с учетом этого интеграл фурье можно записать в виде

_

F(t) =  S()e ^jt d.

^

Пример 2

0 при t < 0

F(t) =

e^-bt при t > 0

_{ }

S() = [ e^-bt e^-jt dt ]/[2] = [  e^-(b+j)t dt ]/[ 2] =

^{ }

_{ }

= -e-t/[2 (b+j)] = -[0 - 1]/[2(b+j)] =

^

= 1/[2(b + j)] = [b - j]/[2(b² + ²)].

_

F(t) =  [b - j]e^-jt/[2(b² + ²)]d =

^

_{ }

= [ [bcos(t)]/[b² + ²]d - j  [sin(t)]/[b² + ²]d]/[2]. (6.2)

^{ }

Пример 3

0 при t  0

F(t) = {

1 при t > 0

При b  0 в примере 2 F(t)  1 при t > 0.

Тогда в соответствии с выражением (6.2) можно записать выражение

_

1(t) = 1/2 +  [sin(t)/ ]d/.

⁰

Исходя их рассмотренных зависимостей Фурье предложено интеграль­ное преобразование

_

F(j) =  F(t)e^-jt dt - прямое преобразование Фурье;

^-

_

F(t) = [ F(j)e^jt d ] - обратное преобразование Фурье.

^-

В соответствии с формулой Эйлера можно прямое преобразование Фурье представить в виде

_

F(j) =  F(t)[cos(t) - jsin(t)] dt.

^-