Лекция № 12 Связь методов исследования непрерывных и дискретных сау

(w- преобразование)

Устойчивость дискретных САУ, как и непрерывных, можно оценить по ее передаточной функции. По виду корней характеристического уравнения можно определить устойчивость системы, а также колебательность переходной функции. Устойчивость непрерывной САУ определяется по расположению корней характеристического уравнения на комплексной плоскости. Корни характеристического уравнения устойчивой непрерывной системы расположены в левой части комплексной плоскости (рис. 12.1).

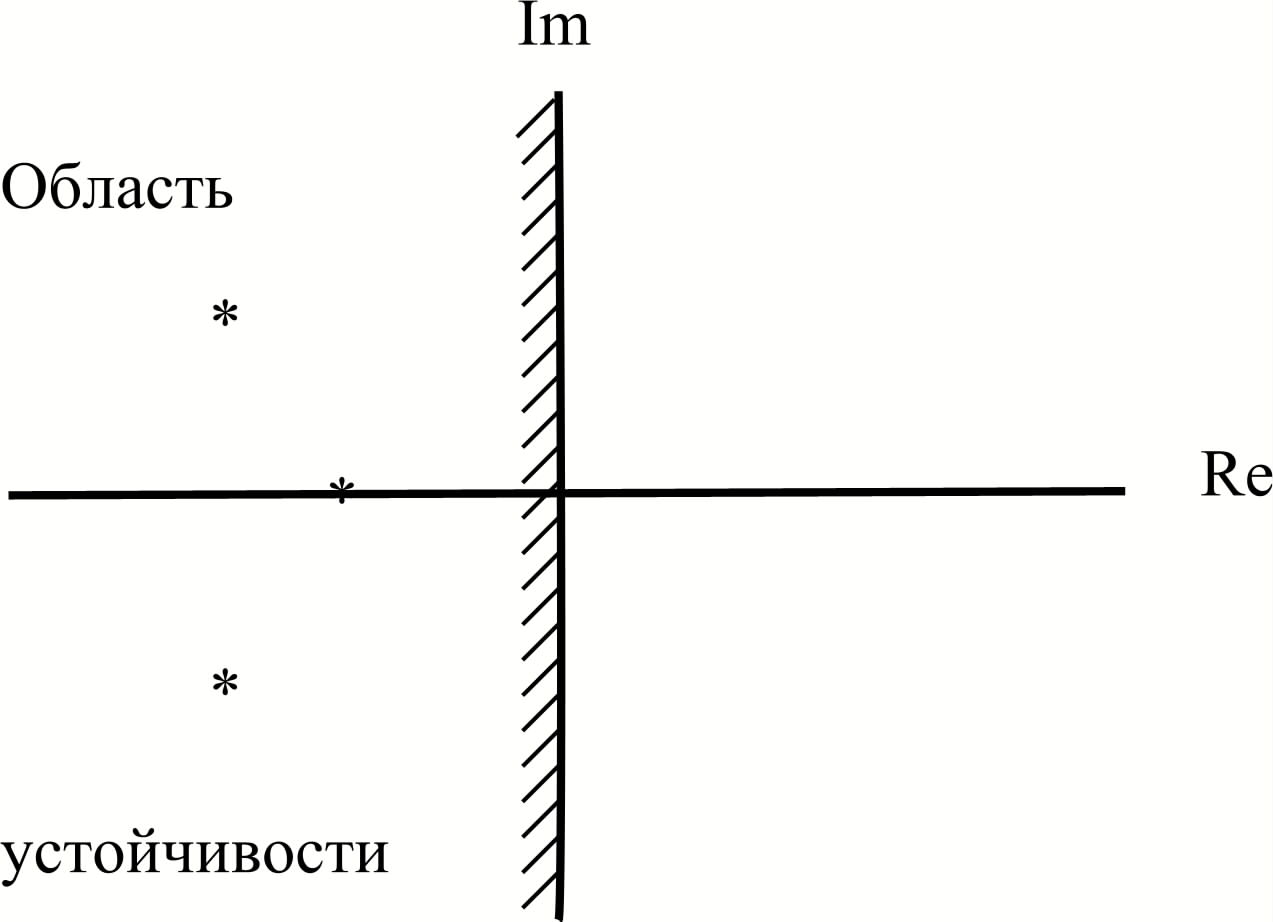
Рис. 12.1. Область устойчивости непрерывной САУ

Поскольку аргументом дискретной передаточной функции является оператор z = e ^pTп , где «p = j», левая полуплоскость комплексной плоскости «сворачивается» в круг единичного радиуса (рис. 12.2), поскольку оператор «z» можно записать в следующем виде.

z = e ^jTп = cos(T_П) + jsin(T_П) = cos() + jsin(), (12.1)

где  – физическая частота;  = T_П – безразмерная частота.

Условием устойчивости дискретной САУ является тот факт, что все корни ее характеристического уравнения должны лежать внутри единичного круга, т.е. |z_i| < 1. Если хотя бы один корень расположен за пределами единичного круга, то система неустойчива. Если же хотя бы один корень равен нулю, то система находится на границе устойчивости.

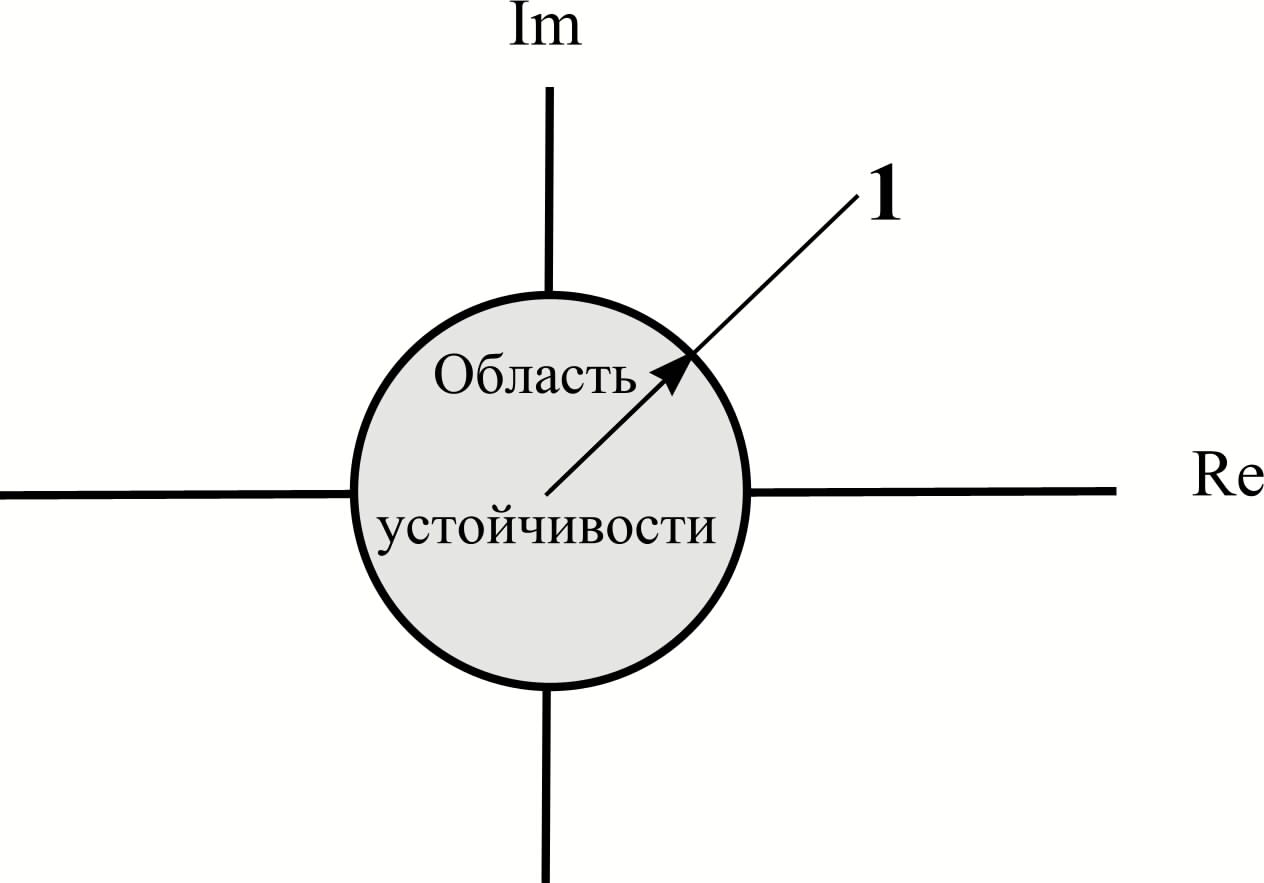
Рис. 12.2. Область устойчивости дискретной САУ

Пример

Пусть дискретная САУ характеризуется передаточной функцией вида:

W(z) = 0,09/(z² – z + 0,09).

Тогда характеристическое уравнение можно записать следующим образом:

D(z) = z² – z + 0,09 = 0.

Корни характеристического уравнения можно найти по теореме Виетта

z = 0,5  [(1/2)² – 0,09]^1/2 = 0,5  [0,16]^1/2 = 0,5  0,4 < 1. (12.2)

На основании выражения (12.2) можно утверждать, что исследуемая система устойчива |z| < 1.

К сожалению, использование других известных критериев (алгебраический, Михайлова, Найквиста и т.д.) для оценки устойчивости дискретной САУ невозможно из-за искажения комплексной плоскости.

Однако преобразование комплексной переменной «z» к другой комплексной переменной «w» позволяет вновь «развернуть» внутреннюю область круга (рис. 4.5.2) в левую полуплоскость (аналогичную показанной на рис. 4.5.1), что дает возможность применять критерии устойчивости непрерывных САУ для оценки устойчивости дискретных САУ.

Прямое и обратное преобразование комплексных переменных производится по формулам:

z = (1 + w)/(1 – w); (12.3)

w = (z – 1)/(z + 1). (12.4)

Пример

Пусть дискретная САУ характеризуется передаточной функцией вида:

W(z) = 0,09/(z² – z + 0,09).

Тогда характеристическое уравнение можно записать следующим образом:

D(z) = z² – z + 0,09 = 0.

После преобразования характеристического уравнения по формуле (12.3) оно принимает вид:

D(w) = [(1 + w)/(1 – w)]² – (1 + w)/(1 – w) + 0,09 = 0. (12.5)

Уравнение (12.5) можно преобразовать к квадратному уравнению, умножив левую и правую части этого уравнения на (1 – w)².

D(w) = (1 + w)² – (1 + w)(1 – w) + 0,09(1 – w)² =

= w² + 2w + 1 – 1 + w² + 0,09 – 0,18w + 0,09w² =

= 2,09 w² + 1,82w + 0,09 = 0. (12.6)

Преобразованное характеристическое уравнение (12.6) позволяет оценивать устойчивость дискретной САУ с помощью критериев применяемых к линейным САУ.

1. Корневой критерий устойчивости требует, чтобы все корни характеристического уравнения были отрицательны.

D(w) = 2,09 w² + 1,82w + 0,09 = 0. (12.7)

w₁ = - 0,053; w₂ = - 0,818, т.е. w_1,2 < 0. Следовательно, система устойчива.

2. Алгебраический критерий устойчивости требует, чтобы: а) выполнялось необходимое условие (все коэффициенты характеристического уравнения были бы положительны); б) выполнялось достаточное условие (все диагональные миноры определителя Рауса – Гурвица также были бы положительны).

a) 2,09 > 0; 1,82 > 0; 0,09 > 0;

|1,82 0,00|

б) M = | |; ₁ = 1,82 > 0; ₂ = 1,820,09 – 0,002,09 = 0,1638 > 0.

|2,09 0,09|

3. Критерий А.В. Михайлова формулируется так: если годограф характеристического многочлена (12.7) начинаясь на положительной части вещественной оси проходит последовательно против часовой стрелки число квадрантов равное порядку передаточной функции системы, то она устойчива. При нарушении хотя бы одного из перечисленных условий система неустойчива. При прохождении годографа через начало координат система находится на границе устойчивости.

В приведенном примере характеристический многочлен представлен в следующем виде:

D(w) = 2,09 w² + 1,82w + 0,09.

Поскольку в соответствии с формулой (12.4) оператор «w» является мнимой частотой характеристический много записать в виде

D(j) = 2,09 (j)² + 1,82(j) + 0,09.

или

D(j) = (0.09 – 2,09)² + 1,82j = U() + jV(). (12.8)

Изменяя  от нуля до , можно построить годограф характеристического многочлена (12.8).

	0	1	
U()	0,09	-2,00	-
V()	0	1,82	

Из таблицы видно, что годограф, начинаясь на положительной ветви действительной оси, проходит последовательно против часовой стрелки два квадранта, следовательно, система устойчива.

Критерий Найквиста позволяет судить об устойчивости замкнутой системы по ее передаточной функции в разомкнутом состоянии.

W_p(z) = W₃(z)/[1 – W₃(z)] = 0,09/(z² - z).

W_p(w) = [0,09(1 – w)²]/[(1 + w)² – (1 – w²)] =

= (0,09 – 0,18w + 0,09w²)/(2w + 2w²).

W_p(j) = (0,09 – 0,18j – 0,09²)/(2j – 2²) =

= (0,09² + 0,18j – 0,09)/[2(² – j)] =

= [(0,09² + 0,18j – 0,09)(² + j)]/[2²(² + 1)] =

= [0,045(² – 3)]/[² + 1] + j[0,045(3² – 1)]/[(² + 1)] = U() + jV().

	0	1/3	1	
U()	-0,135	-0,09	-0,9975	0,045
V()		0	0,045	0

Как видно из таблицы при пересечении вещественной оси А() = U() < -1, т.е. годограф не охватывает точку с координатами (-1, j0), следовательно система устойчива.