1-й семестр / Комплексные числа
.docxФормы записи комплексных чисел
-
Алгебраическая форма комплексного числа – это запись комплексного числа z в виде:
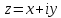
где
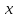 и
и
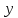 – действительные числа,
– действительные числа,
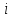 – мнимая единица, удовлетворяющая
соотношению
– мнимая единица, удовлетворяющая
соотношению
 .
Число
.
Число
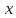 называется действительной частью
комплексного числа
называется действительной частью
комплексного числа
 и имеет обозначение
и имеет обозначение
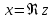 .
Число
.
Число
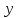 называется мнимой частью комплексного
числа
называется мнимой частью комплексного
числа
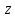 и имеет обозначение
и имеет обозначение
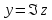 .
.
Комплексное число
считается записанным корректно, если
записано именно в данном виде. Запись
по типу:
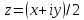 – ошибка. Правильный вариант:
– ошибка. Правильный вариант:
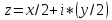 .
.
Чтобы изобразить
комплексное число
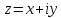 на комплексной
плоскости необходимо, в первую очередь,
изобразить саму плоскость, представляющую
из себя обычную координатную плоскость,
но с осями
на комплексной
плоскости необходимо, в первую очередь,
изобразить саму плоскость, представляющую
из себя обычную координатную плоскость,
но с осями
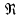 (вместо
(вместо
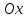 )
и
)
и
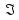 (вместо
(вместо
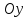 ),
на первой оси отметить значение
),
на первой оси отметить значение
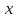 ,
на второй – значение
,
на второй – значение
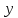 .
Пересечение перпендикуляров к этим
точкам и есть число
.
Пересечение перпендикуляров к этим
точкам и есть число
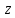 .
.
-
Тригонометрическая форма комплексного числа
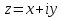 ,
не равного нулю, –
это запись:
,
не равного нулю, –
это запись:
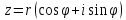
Где
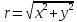 –
модуль комплексного числа, а угол
–
модуль комплексного числа, а угол
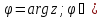 .
Аргумент
.
Аргумент
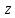 находится следующим образом:
находится следующим образом:

Чтобы изобразить
комплексное число
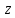 на комплексной
плоскости необходимо из начала координат
провести прямую под углом
на комплексной
плоскости необходимо из начала координат
провести прямую под углом
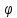 и
отложить на ней расстояние
и
отложить на ней расстояние
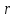 .
Конец
отрезка есть число
.
Конец
отрезка есть число
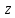 .
.
Короче
говоря, число
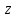 на комплексной плоскости задает вектор
с координатами
на комплексной плоскости задает вектор
с координатами
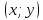 ,
длиной
,
длиной
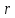 и
углом наклона к оси
и
углом наклона к оси
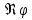 .
.
-
Показательная форма комплексного числа – выражение:
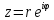
где
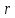 – модуль комплексного числа,
– модуль комплексного числа,
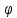 –
его аргумент,
–
его аргумент,
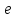 –
экспонента,
–
экспонента,
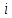 –
мнимая единица. По формуле Эйлера:
–
мнимая единица. По формуле Эйлера:
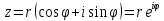
Сопряженные комплексные числа
Комплексны
числа
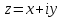 и
и
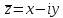 называются
сопряженными.
называются
сопряженными.
-
в тригонометрической форме:
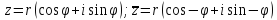
-
в показательной форме:
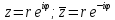
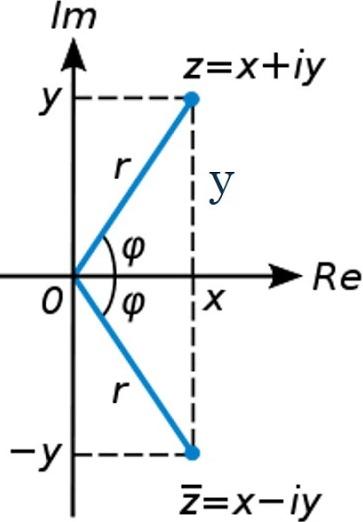
Геометрический смысл:
сопряженное числу
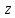 есть число, симметричное
самому числу
есть число, симметричное
самому числу
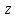 относительно оси
относительно оси
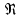 .
.
Свойства операции сопряжения:
-
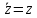 ;
; -
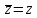 тогда и только
тогда, когда
тогда и только
тогда, когда
 – комплексное число;
– комплексное число; -
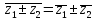
-

-
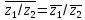
-
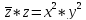
Действия с комплексными числами
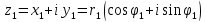 ;
;
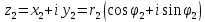
Равенство комплексных чисел:
-
В алгебраической форме:
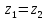 ,
если
,
если
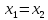 и
и
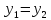
-
В тригонометрической форме:
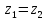 ,
если
,
если
 и
и
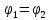
Сложение комплексных чисел:
-
В алгебраической форме:
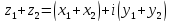 (аналогично с вычитанием)
(аналогично с вычитанием)
-
В тригонометрической форме:
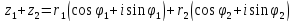 (аналогично с вычитанием)
(аналогично с вычитанием)
Умножение комплексных чисел:
-
В алгебраической форме:
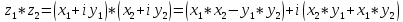 (простое раскрытие
скобок)
(простое раскрытие
скобок)
-
В тригонометрической форме:
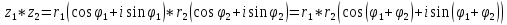
Деление комплексных чисел:
-
В алгебраической форме:
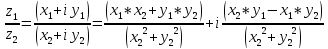 (раскрытие скобок с
помощью домножения знаменателя на
сопряженное)
(раскрытие скобок с
помощью домножения знаменателя на
сопряженное)
-
В тригонометрической форме:
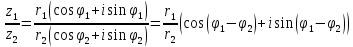
Возведение
комплексного числа в степень
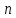
-
в тригонометрической форме (формула Муавра):
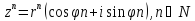
-
в показательной форме:
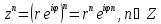
Важно
помнить, что аргумент
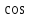 и
и
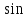 должен находиться в диапазоне
должен находиться в диапазоне
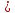 ,
следовательно,
нужно не забыть вычесть нужное количество
,
следовательно,
нужно не забыть вычесть нужное количество
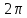 после
домножения.
после
домножения.
Извлечение корня из комплексного числа
Чтобы извлечь корень из комплексного числа, в первую очередь, нужно представить его в тригонометрической форме. Количество корней есть значение, равное степени корня. То есть, извлекая корень 4-й степени из комплексного числа, мы получаем 4 корня.
Как и для возведения в целую степень, будет справедливо:
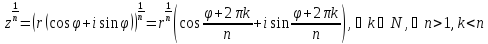
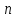 – степень извлекаемого
корня,
– степень извлекаемого
корня,
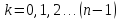 .
Вычисляем извлеченные корни поочередно,
в каждый из которых подставляем свое
значение n. Важно
помнить, что аргумент
.
Вычисляем извлеченные корни поочередно,
в каждый из которых подставляем свое
значение n. Важно
помнить, что аргумент
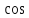 и
и
 должен находиться в диапазоне
должен находиться в диапазоне
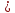 ,
следовательно,
нужно не забыть вычесть нужное количество
,
следовательно,
нужно не забыть вычесть нужное количество
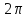 после
всех операций вычисления.
после
всех операций вычисления.
Если
комплексное число не равно нулю, то
корни степени
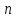 существуют
всегда, и их можно изобразить на
комплексной плоскости: они будут
представлять собой вершины правильного
существуют
всегда, и их можно изобразить на
комплексной плоскости: они будут
представлять собой вершины правильного
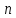 -угольника, который вписан в окружность
с центром в начале координат и радиусом
-угольника, который вписан в окружность
с центром в начале координат и радиусом
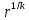 .
.
Свойства комплексных чисел
-
Переместительное свойство:
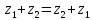 ;
;
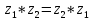
-
Сочетательное свойство:
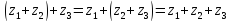 ;
;
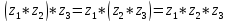
-
Распределительное свойство: